Что такое натуральные числа в математике

Начиная с детского возраста, когда ребенок пытается сосчитать, сколько перед ним предметов, он пользуется натуральными числами. А, перечисляя их в возрастающем порядке, строит натуральный ряд. Однако делает он это неосознанно, в отличие от счета в арифметике, который опирается на целый ряд четко обозначенных понятий.

Что такое натуральные числа

Термин «натуральный» произошел от латинского naturalis, что обозначает «естественный». На самом деле, что может быть естественнее обычного перечисления чисел, следующих одно за другим? Множество таких чисел характеризуется бесконечностью, потому что всегда есть число, большее, чем предыдущее. Если обозначить любое число через a, то в ряду натуральных чисел всегда есть a+1 и a-1, если a не равно 1.

Сосчитать предметы можно только целым числом, поэтому натуральные числа представлены множеством целых чисел. Каким же образом можно подойти к ответу на вопрос: «Является ли натуральным число со знаком «минус»? Ведь оно тоже целое. Нет, отрицательным числом сосчитать предметы невозможно, поэтому оно не является натуральным.

Рассмотрим столбик термометра, установленного на улице зимой. Допустим, на нем отметка температуры -7^оС. Это отрицательное число, оно не относится к группе натуральных.

Аналогичный пример: на тарелке 4 груши и еще одна половинка. Этой половинкой нельзя сосчитать целую грушу. Это – часть предмета, а, следовательно, дробь. Дроби, как и отрицательные числа, не являются натуральными.

Другими словами, натуральным есть число, которое возникает при счете. Оно дает представление о количестве рассматриваемых предметов, позволяет представить их с закрытыми глазами.

Примеров последовательности натуральных чисел, расположенных в ряду в порядке возрастания и поэтому являющихся натуральным рядом, существует бесконечное множество. В окружающем мире всегда находятся предметы, подлежащие счету, а расположение цифр в порядке возрастания - реальная возможность получить натуральный ряд. 

Источник: fsd.kopilkaurokov.ru

С натуральными числами можно производить различные действия: сложение, вычитание, умножение, деление. В результате трех первых получаются натуральные числа. Например:

5+2=7

8-4=4

4*3=12

Однако при делении натурального числа на натуральное, частное не всегда целое число.

Наименьшее натуральное число

Натуральный ряд имеет свое начало. Это единица. Однако нельзя назвать самое большое натуральное число, поскольку в любом случае число-последователь может быть на единицу больше.

Например, на дереве сидит 5 ворон. Считая их, ученик образовал натуральный ряд. Какое из чисел этого ряда будет наименьшим? Конечно, 1, поскольку меньше, чем одна ворона не может сидеть на дереве.

Часто задают вопрос: ведь нуль меньше единицы? Значит, он — наименьшее число. Это неверное утверждение. Поскольку нулем невозможно считать, он не обозначает количество предметов. Однако нуль может использоваться для записи натуральных чисел, обозначая пропуск разряда: 502, 45206, 789201 и т.п.

Свойства натуральных чисел

Натуральные числа, как математическое понятие, характеризуются рядом свойств. Это:

• отношение следования;
• особенности сложения;
• особенности вычитания;
• особенности умножения;
• особенности деления;
• особенности умножения в выражениях, имеющих в своем составе вычитание (сложение);
• особенности деления в выражениях, имеющих в своем составе вычитание (сложение);
• особенности сравнения;
• особенности округления.

Отношение следования для множества натуральных чисел означает, что оно начинается с нуля и продолжается бесконечно. При этом взятое для примера любое число этого натурального ряда на единицу меньше последующего.

При сложении двух натуральных чисел действуют законы:

1. Переместительный (от перемещения слагаемых сумма не меняется): 5+2=2+5.
2. Сочетательный: (одно слагаемое, вынесенное за скобку, может выть внесено в нее с неизменным результатом): (2+3)+5=2+(3+5).

Аналогичные законы действуют для умножения: переместительный (3*4=4*3) и сочетательный (3*4)*5=3*(4*5).

Если натуральное число разделить на 1, то его вид не изменится: 5:1=5, 10:1=10.

Если же произвести деление на само это число, частное будет равно 1: 25:25=1

Особенности умножения в выражениях, имеющих в своем составе вычитание (сложение), сводятся к сочетательному закону: 5*(4-2)=5*4-5*2 или 6*(3+4)=6*3+6*4.

Порядок решения примеров, содержащих деление и сложение (вычитание) аналогичен: (4+6):2=4:2+6:2 или (9-6):3=9:3-6:3.

Для сравнения чисел действует правило: из двух натуральных чисел меньшим является то, которое в натуральном ряду стоит левее (то есть при счете появляется раньше).

Существует более сложное правило для сравнения двух чисел. С ними производят действие вычитания. Если в результате получилось число, больше нуля, значит второе число больше первого.

Когда особая точность при решении задач не нужна, прибегают к округлению натуральных чисел до разрядов. Так, число 54 можно округлить до 50, а 182 — до 180. Чтобы найти то число, до которого можно округлить, нужно обратить внимание на последнюю цифру. Если она больше либо равна 5, округление происходит до предыдущего десятичного разряда (для 564 искомой цифрой округления является 560, для 4827 — 4830).

Обозначение натуральных чисел

В математике принято классифицировать натуральные числа по разрядам, которые определяются количеством знаков в них. Так, единицы — это 1,2,3,4,5 …9. Эти же цифры с прибавленным нулем справа обозначают десятки: 10, 20, 30…90.  Несложно понять, что цифры с двумя нулями обозначают сотни: 100, 200, 300, 400…900. Когда идет счет на тысячи, применяются цифры с тремя нулями: 1000, 2000, 3000, 4000…9000.

Количество таких разрядов, применяемых в обычных ситуациях, — 15. Таким образом, доходят до обозначения триллионов.

В то же время это не значит, что цифры могут заканчиваться только на нули. Разрядность действует во всех случаях, обозначающих количество предметов. Например, вид числа 5 252 436 можно прочитать так: 5 миллионов 252 тысячи 436.

Такой подход единообразен для каждой точки земного шара. Именно поэтому пользоваться натуральным рядом для счета удобно. Для любого человека математическое выражение, включающее десятичную систему исчисления, имеет одинаковое значение.

Принято, что обозначаться множество натуральных чисел в целом должно буквой N.

Источник: www.uznaychtotakoe.ru

Что такое натуральный ряд чисел

Источник: cf3.ppt-online.org

Счет предметов был нужен людям постоянно, начиная с древнего мира. В начале цифры заменялись зарубками на дереве. По окончании работы их считали и сравнивали с предыдущим результатом.

Использовать цифры впервые стали в Египте и Месопотамии. Произошло это около 5 тысячелетий назад. Необходимость в счете возникла по мере развития животноводства и земледелия и необходимости учета результатов своего труда.

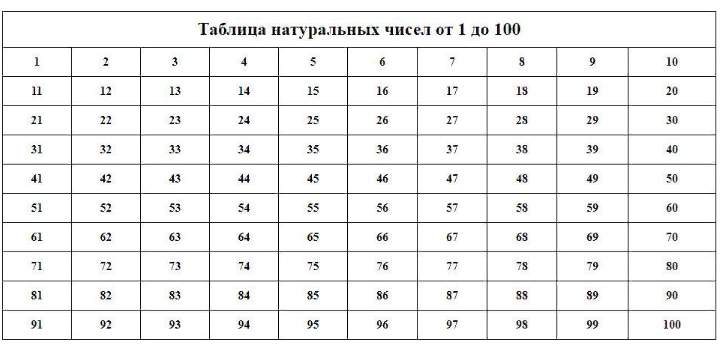
В отличие от древнего мира, у нас нет необходимости класть в мешок столько камушков, сколько родилось овец в выбранный день. У нас есть цифры, которые можно выстроить в определенную последовательность, например, от 1 до 100.

Источник: deepcloud.ru

В таблице вынесены числа, образующие натуральный ряд, поскольку выстроены они в порядке возрастания.

Начинаясь с единицы, натуральный ряд может продолжаться бесконечно долго. В это же время, перед единицей чисел нет, поскольку она — наименьший представитель такого ряда.

Имея перед глазами такой ряд, всегда можно назвать числа, заключенные в промежутке между двумя названными. Например, между 6 и 9 заключены 7 и 8. Они меньше 9, но больше 6. Между 1 и 10 располагаются 2, 3, 4, 5, 6, 7, 8. Все названные числа меньше 9 и больше 1.

Таким образом, существует закономерность: выбранные числа натурального ряда всегда больше тех, которые находятся в этом ряду слева от них и меньше тех, что справа.

Анализируя приведенный ряд, можно сделать еще один вывод: по мере увеличения расстояния выбранного числа от единицы, растет его разрядность, достигая огромных величин, пределы которым отсутствуют. И, наоборот, по мере движения вдоль ряда чисел влево, разрядность падает.

Однозначные, двузначные, трехзначные, многозначные натуральные числа

Цифры — это знаки, выражающие количество. В арифметике существует ряд цифр, с помощью которых можно обозначить любое число. Этот ряд выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Например, число 689 состоит из цифр 6, 8 и 9, а Число 25568963 — из цифр 2, 5, 6, 8, 9, 3.

Из примеров видно, какое бы большое число необходимо обозначить, используются все те же девять цифр, только в определенной последовательности. Бывают случаи, что некоторые из них могут повторяться, а некоторые — отсутствовать вовсе.

Числа, для обозначения которых используется одна цифра, называются однозначными. Это, собственно, и есть основные девять цифр. Если необходимо отобразить на бумаге, что мальчику тринадцать лет, пишут двузначное число 13. Говоря о том, что в одной тонне тысяча килограмм, на бумаге записывают трехзначное число 1000.

Таким образом, одно-, дву-, трех- или многозначное число перед глазами, определяется количеством задействованных цифр.

При очень большом количестве цифр, говорят о многозначности этого числа.

Бывает, что при решении задач однозначные числа переходят в двузначные. Например:

Две сестры собирали маме букет. Одна из них сорвала 5 роз, другая — 7. Для обеих девочек количество цветов обозначается однозначным числом. Сложив цветы в один букет, их количество стало 12. Следовательно, число перешло в разряд двузначных.

Источник: fsd.kopilkaurokov.ru