Формулы квадрата суммы и квадрата разности

Что такое квадрат разности

С помощью специальных математических формул значительно упрощаются действия с многочленами. К примеру, предусмотрены соотношения, благодаря которым допустимо сократить умножение. С такими выражениями школьники знакомятся на уроках алгебры в классах средней школы. Путем обыкновенных корректных преобразований удается справиться с самыми сложными задачами по математике. Наиболее распространенными являются формулировки свойства квадрата разности и квадрата суммы.

Формула

Выражение для вычисления квадрата разности можно вывести путем последовательного выполнения логичных преобразований. Представим, что имеется некое выражение, содержащее пару членов и знак минуса, то есть разность:

\((р-q)\)

Попробуем возвести во вторую степень записанное выражение. Получим квадрат разности:

\((р-q) ^2\)

Заметим, что многочлен во второй степени означает, что данный многочлен был умножен сам на себя:

\((р-q) (р-q)\)

Выполним умножение почленно, получим:

\(р(р-q) - q(р-q)\)

Далее целесообразно избавиться от скобок. В таком случае, исходное выражение примет следующий вид:

\(р^2-рq-рq+q^2\)

Выполним дальнейшие преобразования, чтобы получить окончательный ответ:

\(р^2-2рq+q^2\)

В результате простых арифметических действий была записана формула сокращенного умножения, которую называют квадратом разности:

\((р-q) ^2 = р^2-2рq+q^2\)

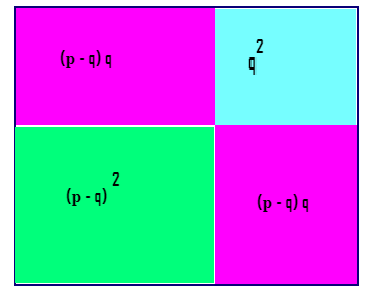
Математическое соотношение, называемое квадратом разности, можно объяснить с точки зрения геометрии. Представим, что имеется некий квадрат, сторона которого равна р. Впишем в этот прямоугольник другой квадрат меньшего размера со стороной, соответствующей q.

 

Попробуем определить, чему равна площадь рассматриваемой геометрической фигуры. Воспользуемся формулой вычисления площади в случае квадрата:

\(р^2 = (р – q)^2 + q^2 + 2(р – q)q\)

Выполним соответствующие преобразования, чтобы упростить полученный многочлен:

\((р-q)^2 = р^2-q^2-2(р-q)q = р^2-q^2-2рq+2q^2 = р^2-2рq+q^2\)

В результате получилось с помощью геометрических закономерностей вывести формулу разности квадратов, которая ранее была выведена путем алгебраических вычислений.

В процессе решения задач с помощью формул упрощенного умножения важно помнить о слагаемом, которое стоит на втором месте в выражении с двучленами. Необходимо строго соблюдать правила работы со знаками плюса и минуса.

Примеры

Решение

\((m-n)^2 = m^2-2mn+n^2\)

\((x-5)^2 = x^2-2x\cdot5+5^2 = x^2-10x+25\)

\((7y-9z)^2 = (7y)^2-2\cdot7y\cdot9z+(9z)^2 = 49y^2-126yz+81z^2\)

\((3km^2-8n^2 )^2 = (3km^2 )^2-2\cdot3km^2\cdot8n^2+(8n^2 )^2 = 9k^2 m^4-48km^2 n^2+64n^4\)

Ответ: \(m^2-2mn+n^2; x^2-10x+25; 49y^2-126yz+81z^2; 9k^2 m^4-48km^2 n^2+64n^4.\) 

Решение

\((10m-1)^2+20m = (10m)^2-2\cdot10m\cdot1+1+20m = 100m^2-20m+1+20m = 100m^2+1\)

\(36k^2-(1-6k)^2 = 36k^2-(1-2\cdot6k+(6k)^2 ) = 36k^2-1+12k-36k^2 = 12k-1\)

\(4(x-1)-(2x+1)^2 = 4x-4-((2x)^2+2\cdot2x+1) = 4x-4-4x^2-4x-1 = -4x^2-5\)

\(\frac{1}{3} (3y+4)^2-8y = \frac{1}{3} ((3y)^2+2\cdot3y\cdot4+4^2 )-8y = \frac{1}{3} (9y^2+24y+16)-8y =3y^2+8y+\frac{16}{3}-8y=3y^2+5 \frac{1}{3}\)

Ответ: \(100m^2+1; 12k-1; -4x^2-5; 3y^2+5 \frac{1}{3}.\) 

Решение

\((7-x)^2-(x+8)^2 = 45\)

\(49-14x+x^2-(x^2+16x+64) = 45\)

\(49-14x-16x-64 = 45\)

\(-30x = 45-49+64\)

\(-30x = 60\)

\(x = -2\)

\((2x-15)^2-x(4x+3) = 153\)

\((2x)^2-2\cdot2x\cdot15+15^2-4x^2-12x = 153\)

\(-60x+225-12x = 153\)

\(-72x = 153-225\)

\(-72x = -72\)

\(x = 1\)

Ответ: \(x = -2; x = 1.\) 

Решение

\((x^2 + 3x - 4y)^2 - x^4 - 9x^2 - 16y^2 = (х^2)^2 + (3х)^2+(-4у)^2 + 2 \cdot х^2 \cdot 3х + 2 \cdot х^2 \cdot (-4у) + 2\cdot 3х \cdot (-4у) - х^4 - 9х^2 – 16у^2 = х^4 + 9х^2 +16у^2 + 6х^3 - 8х^2у – 24ху - х^4 -9х^2 -16у^2 = 6х^3 – 8х^2у – 24ху\)

Ответ: \(6х^3 – 8х^2у – 24ху.\)

 

Решение

\((9 − x)^2 = (9 − x)^2 = 9^2 − 2 \cdot 9 \cdot x + x^2 = 81 − 18x + x^2\)

\((x − 25)^2 = (x − 25)^2 = x^2 − 2 \cdot x \cdot 25 + 25^2 = x^2 − 50x + 625\)

\((3x^2 − y^3)^2 = (3x^2 − y^3)^2 = (3x^2)^2 − 2 \cdot 3x^2 \cdot y^2 + (y^3) ^2 = 9x^4 − 6x^2y^3 + y^6\)

Ответ: \(81 − 18x + x^2; x^2 − 50x + 625; 9x^4 − 6x^2y^3 + y^6.\)

Что такое квадрат суммы

Формулы сокращенного умножения, в том числе, квадрат суммы, позволяют значительно сократить количество вычислений при решении разнообразных задач по алгебре, физике, геометрии и другим дисциплинам. С помощью справедливых закономерностей громоздкие записи приобретают читабельный вид. Оперируя данными правилами, получается максимально рационально производить расчеты в процессе приведения дробных чисел к единому знаменателю. Подобные навыки полезны, когда нужно найти решение примеров на определение параметров геометрических фигур, вычислить значения тригонометрических функций,  произвести операции по математическому анализу, упростить записи химических реакций, подготовить характеристики экономических показателей.

Формула

Представим, что имеется некое выражение, состоящее из пары значений, разделенных знаком плюса:

\((р + q)\)

Попробует возвести во вторую степень данное выражение, то есть представить сумму в квадрате:

\((р+q)^2 = (р+q)(р+q) = р(р+q)+q(р+q) = р^2+рq+рq+q^2 = р^2+2рq+q^2\)

Таким образом, получилось выражение для вычисления квадрата суммы:

\((р+q)^2 = р^2+2рq+q^2\)

С помощью записанной формулы сокращенного умножения можно существенно упростить себе задачу, решая примеры по алгебре. В результате отпадает необходимость в перемножении всех скобок и множественном приведении подобных слагаемых, что в итоге приводит к сокращению числа слагаемых с четырех до трех.

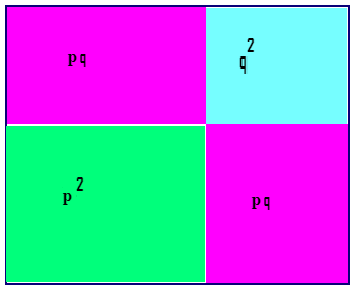
Рассмотрим представленную закономерность с точки зрения геометрии. Начнем с изображения прямоугольника, стороны которого равны \((р + q)\) . В результате получим квадрат:

 

Заметим, что данная геометрическая фигура включает в себя пару квадратов и пару прямоугольников. Таким образом, чтобы вычислить ее площадь, потребуется найти сумму площадей всех фигур, входящих в ее состав:

\(S = (р+q)^2 = р^2+q^2+2рq\)

В результате получилось представить доказательства в виде геометрического обоснования формулы квадрата суммы.

Рассматриваемую закономерность справедливо применять к выражениям, которые состоят из более двух слагаемых. В процессе вычислений квадрата такой суммы потребуется найти вторую степень каждого из компонентов выражения, далее представить умноженные на два произведения, которые можно получить, а затем суммировать промежуточные итоги расчетов.

Примеры

Решение

\((x+y)^2 = x^2+2xy+y^2\)

\((3+t)^2 = 3^2+2\cdot3t+t^2 = 9+6t+t^2\)

\((3a+4b)^2 = (3a)^2+2\cdot3a\cdot4b+(4b)^2 = 9a^2+24ab+16b^2\)

\((4k^2 m+5n)^2 = (4k^2 m)^2+2\cdot4k^2 m\cdot5n+(5n)^2 = 16k^4 m^2+40k^2 mn+25n^2\)

\((5x^2+7y)^2 = (5x^2 )^2+2\cdot5x^2\cdot7y+(7y)^2 = 25x^2+70x^2 y+49y^2\)

Ответ: \(x^2+2xy+y^2; 9+6t+t^2; 9a^2+24ab+16b^2; 16k^4 m^2+40k^2 mn+25n^2; 25x^2+70x^2 y+49y^2.\)

 

Решение

Заметим, что в данном случае вторые степени выражений записаны вторым и третьим номером, считая слева. По этой причине целесообразно сделать перестановку слагаемых и воспользоваться уже знакомой формулой сокращенного умножения:

\(28ху + 49х^2 + 4у^2 = 49х^2 + 28ху + 4у^2 = (7х)^2 + 2 \cdot 7х \cdot 2у +(2у)^2 = (7х + 2у)^2\)

Ответ: \((7х + 2у)^2.\)

 

Требуется вычислить значение данного выражения.

Решение

Заметим, что в этом случае целесообразно применить формулу сокращенного умножения для каждого из представленных выражений, чтобы возвести число в квадрат. Затем можно найти сумму промежуточных итогов вычислений.

\(103^2 + 197^2 = (100 + 3)^2 + (200 – 3)^2 = 100^2 + 2 \cdot 100 \cdot 3 + 3^2 + 200^2 – 2 \cdot 200 \cdot 3 + 3^2 = 10000 + 600 + 9 + 40000 – 1200 + 9 = 50000 – 600 + 18 = 49418\)

Ответ: 49418.

Решение

\((5a + 3)^2 = (5a)^2 + 2 × 5a × 3 + 32 = 25a^2 + 30a + 9\)

\((5a + 3)^2 = 25a^2 + 30a + 9\)

\((5a + 3)^2 = (5a + 3)(5a + 3) = 25a^2 + 15a + 15a + 9 = 25a^2 + 30a + 9\)

\((m + n)^2 = m^2 + 2mn + n^2\)

\((x + 8)^2= x^2 + 2 \cdot x \cdot 8 + 82 = x^2 + 16x + 64\)

\((2x2 + 3x3)^2 = (2x^2)^2 + 2 \cdot 2x^2 \cdot 3x^3 + (3x^3)^2 = 4x^4 + 12x^5 + 9x^6\)

\((5a + 5)^2 = (5a)^2 + 2 \cdot 5a \cdot 5 + 5^2 = 25a^2 + 50a + 25\)

Ответ: \(25a^2 + 30a + 9; m^2 + 2mn + n^2; x^2 + 16x + 64; 4x^4 + 12x^5 + 9x^6; 25a^2 + 50a + 25.\)

Решение

Заметим, что в данном случае пара слагаемых, которая записана на первом месте слева, схожа с выражением для расчета квадрата суммы. Выполним арифметические преобразования:

\(х^2 – 2 \cdot 2 \cdot х + 2^2 - 2^2 – 5 =0\)

\((х^2 – 2 \cdot 2 \cdot х +2^2) - 2^2 – 5 = 0\)

\((х - 2)^2 = 4 + 5\)

\((х – 2)^2 = 9\)

\(х = 2 = \sqrt{9}\)

\(х = 2 = - \sqrt{9}\)

\(х – 2 = 3\)

\(х – 2 = -3\)

\(х = 5\)

\(х = -1\)

Ответ: \(х_1 = 5, х_2 = -1\)