Как вычисляются координаты вектора
Что такое координаты вектора
Вектором называют некое направление в виде отрезка с определенными в пространстве начальной и конечной точками.
Предусмотрено стандартизированное обозначение вектора. К примеру, если в точке А какой-то вектор берет свое начало, а в точке В — заканчивается, то его записывают таким образом: \(\overrightarrow{AB}\). Допустимо использовать и сокращенный вариант, к примеру: \(\overrightarrow{a}\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: shkolkovo.net
В некоторых случаях уместно сформулировать понятие вектора как передвижение из начальной точки А в конечную точку В. Согласно ранее записанному определению, вектор характеризуется некой длиной. К примеру, для \(\overrightarrow{AB}\) длиной, либо модулем, является протяженность отрезка АВ. Данное утверждение допустимо сформулировать в виде математического соотношения:
\(|\overrightarrow{AB}|=AB\)
Заметим, что не исключены случаи совпадения начальной и конечной точек рассматриваемого вектора. Тогда говорят, что этот вектор является нулевым.
Школьникам и студентам часто приходится иметь дело с векторами. С таким понятием нередко встречаются учащиеся в процессе решения контрольных и самостоятельных работ по геометрии и физике. Как правило, рассматривается декартова координатная система, ориентируясь на которую можно вычислить координаты соответствующего отрезка с конкретным направлением. Процедура заключается в разложении заданного направленного отрезка по базисным векторам.
Принцип основан на фундаментальных знаниях геометрии. В результате получается интерпретировать это действие в виде векторной проекции относительно осей координат. При наличии данных о координатах, которым соответствуют точки начала и конца вектора, представляется возможным рассчитать непосредственно координаты искомого вектора. Процедура подразумевает расчет разности между координатами точки, где вектор заканчивается, и координатами точки, в которой он начинается.
Рассматриваемое действие по идентификации координат вектора целесообразно записать в общей форме таким образом:
\(\overrightarrow {AB}=(AB_{x},AB_{y},AB_{z})=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z})\)
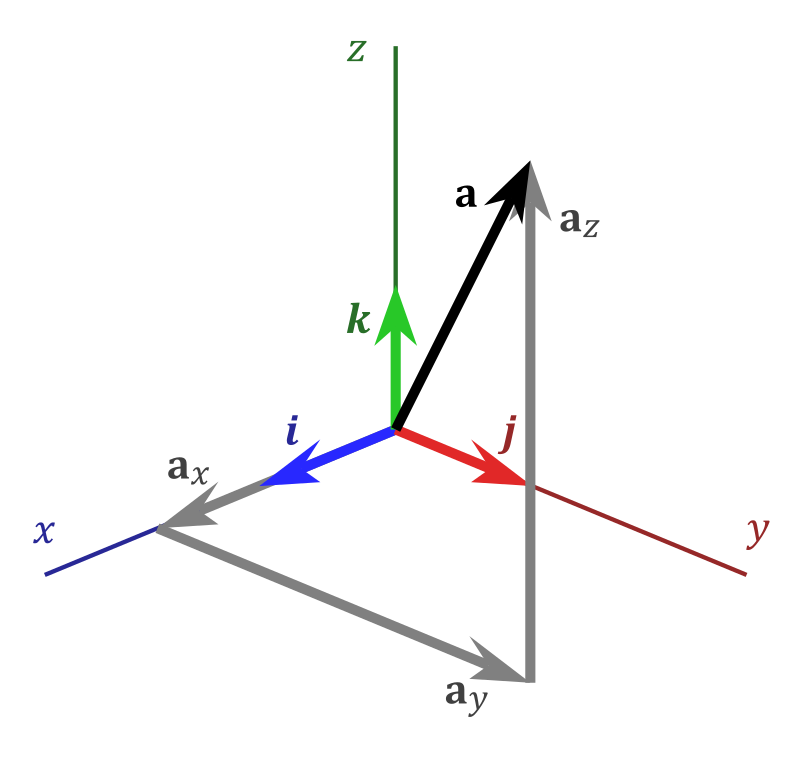
В качестве базиса принято рассматривать орты координат. Для их обозначения используют \({\vec {k}}{\vec {i}},{\vec {j}},{\vec {k}}\), которые соответствуют осям x,y,z. При таких условиях \({\vec {a}}\) допустимо выразить с помощью следующего математического соотношения:
\({\vec {a}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}+a_{z}{\vec {k}}\)
Заметим, что какое-либо свойство в науке геометрии допустимо сформулировать с помощью координат. В результате оно приобретает алгебраическую форму, что позволяет значительно упростить решение тех или иных задач. С другой стороны, несколько некорректно применять обратный принцип действий.
Источник: ru.wikipedia.org
Координаты вектора представляют собой проекции х и у заданного вектора \(\overrightarrow {AB}\) на координатные оси в рамках прямоугольной координатной системы.
В решении задач уже привычно использовать различные закономерности, с помощью которых можно значительно упростить вычисления. В ходе изучения темы координат вектора можно также выделить несколько полезных признаков. Перечислим свойства направленных отрезков:
- В рамках общей координатной системы какие-либо векторы, которые идентичны друг другу, обладают аналогичными координатами.
- Если вектора являются коллинеарными, то их координаты пропорциональны. При этом рассматриваемые вектора не должны обладать нулевым значением.
- Протяженность произвольного вектора во второй степени соответствует результату сложения координат данного вектора, возведенных во вторую степень.
- Произведение некого вектора и числа из множества действительных подразумевает произведение каждой из координат заданного вектора на это число.
- Если требуется суммировать вектора, то следует сложить их координаты.
- Вычисление скалярного произведения пары векторов заключается в сложении произведений координат, которые принадлежат рассматриваемым векторам.
Как найти координаты вектора: формулы
Зная координаты вектора, можно производить с ними разнообразные вычисления. Справедливо и обратное, то есть при известных характеристиках вектора допустимо рассчитать, чему равны его координаты. Рассмотрим ряд полезных соотношений, которые значительно упростят процесс решения заданий на поиск координаты векторов. Начнем с простейшего выражения, позволяющего достаточно быстро определить координаты вектора при известных идентификаторах точек начала и конца:
\(\overline{AB}=\left(x_{2} -x_{1} ;\; y_{2} -y_{1} \right)\)
\(\overline{AB}=\left(b_{1} -a_{1} ;\; b_{2} -a_{2} ;\; b_{3} -a_{3} \right)\)
В качестве примера рассмотрим некий вектор \(\overline{AB}\). Пусть этот вектор начинается в точке \(A\left(3;\; -1\right)\), а заканчивается в точке \(B\left(0;\; 2\right)\). Попробуем вычислить, чему равны координаты такого вектора.
Воспользуемся уже знакомым математическим выражением и найдем ответ к этой задаче:
\(\overline{AB}=\left(0-3;\; 2-\left(-1\right)\right)=\left(-3;\; 3\right)\)
Таким образом:
\(\overline{AB}=\left(-3;\; 3\right)\)
Координаты вектора можно использовать при вычислении протяженности направленного отрезка. Представим, что имеется некий вектор \(\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\)В таком случае справедливым является следующее равенство:
\(\left|\bar{a}\right|=\sqrt{a_{1}^{2} +a_{2}^{2} +a_{2}^{3} }\)
Заметим, что данное соотношение допустимо использовать и тогда, когда требуется рассчитать координаты направленного отрезка.
Попробуем определить, чему равен модуль направленного отрезка, записанного с помощью простого выражения: \(\bar{a}=\left(3;\; 4\right)\)
Воспользуемся ранее изученной формулой, с помощью которой не составит труда определить искомую величину:
\(\left|\bar{a}\right|=\sqrt{3^{2} +4^{2} } =\sqrt{9+16} =\sqrt{25} =5\)
Таким образом:
\(\left|\bar{a}\right|=5\)
Другим вариантом применения координат направленного отрезка является вычисления угла, который расположен между парой векторов. В данном случае целесообразно воспользоваться следующим справедливым равенством:
\(\cos \varphi =\frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|}\)
С целью лучше разобраться в таком достаточно сложном соотношении величин попробуем решить типичный пример. Это поможет наглядно продемонстрировать применение уравнения на практике.
Предположим, что пара произвольных векторов задана следующими координатами: \(\bar{a}=\left(1;\; 1\right) \bar{b}=\left(0;\; 1\right)\) Исходя из условий, требуется вычислить угол, расположенный между этими направленными отрезками.
Запишем выражение для расчета косинуса искомого угла:
\(\cos \varphi =\frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|} \Rightarrow \varphi =\arccos \frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|}\)
В результате получим следующее соотношение:
\(\varphi =\arccos \frac{1\cdot 0+1\cdot 1}{\sqrt{1^{2} +1^{2} } \cdot \sqrt{0^{2} +1^{2} } } =\arccos \frac{0+1}{\sqrt{1+1} \cdot \sqrt{0+1} } =\arccos \frac{1}{\sqrt{2} } = \arccos \frac{\sqrt{2} }{2} =\frac{\pi }{4}\)
Таким образом:
\(\varphi =\frac{\pi }{4}\)
Примеры решения задач
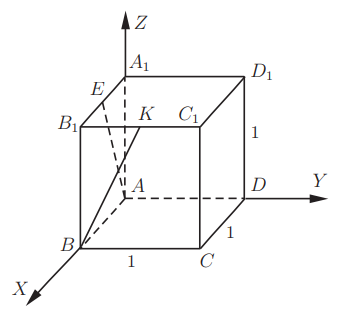
Представим, что имеется некая геометрическая фигура кубической формы. Назовем ее таким образом: ABCDA1B1C1D1. Пусть точки, обозначенные за E и K, делят ребра куба на две равные части, что позволяет получить следующие отрезки: A1B1 и B1C1. Требуется определить величину косинуса угла, роль сторон которого играют прямые AE и BK.
Источник: ege-study.ru
Решение
Кубическая форма данной в задаче фигуры позволяет использовать в расчетах прямоугольную координатную систему, что очень удобно в процессе расчетов. Так как от величины ребер не зависит ответ к этому заданию, допустимо предположить, что она составляет единицу.
Заметим, что прямые, обозначенные за АЕ и ВК являются скрещивающимися. С целью вычисления величины угла, который образуют эти прямые, необходимо знать координаты:
A(0;0;0)
B(1;0;0)
\(E(\frac{1}{2};0;1)\)
\(K(1;\frac{1}{2};1)\)
Затем можно записать координаты рассматриваемых направленных отрезков:
\(\vec{AE}\left (\frac{1}{2};0;1 \right )\)
\(\vec{BK}\left (0;\frac{1}{2};1 \right )\)
С помощью уже знакомой из теоретического раздела формулы не составит труда вычислить искомое значение косинуса угла:
\(\cos\phi = \frac{\overrightarrow{АЕ}\cdot \overrightarrow{ВК}}{\mid\overrightarrow{АЕ}\mid\cdot \mid\overrightarrow{ВК}\mid} = \frac{\frac{1}{2}\cdot 0 + 0\cdot \frac{1}{2} + 1 \cdot 1}{\sqrt{\frac{1}{2}^{2} + 0^{2} + 1^{2}} \cdot \sqrt{\frac{1}{2}^{2} + 0^{2} + 1^{2}}} = \frac{1 \cdot 4}{5} = 0,8\)
Ответ: 0,8.
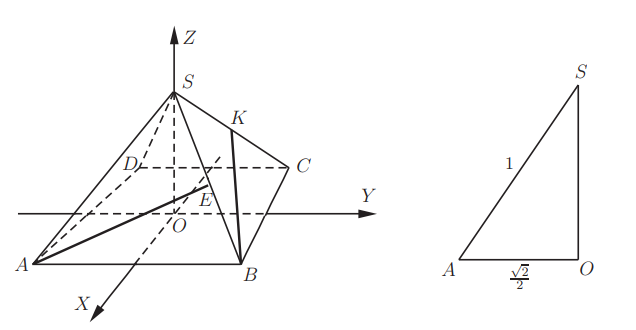
На рисунке изображена четырехугольная пирамида, которая является правильной. Данная фигура обозначена как SABCD. Ребра этой пирамиды соответствуют единице. С помощью точек E и K ребра геометрической фигуры SB и SC делятся на две равные части. Необходимо вычислить величину косинуса угла, роль сторон которого играют прямые AE и BK.
Источник: ege-study.ru
Решение
В первую очередь требуется определиться с местом, где начинается координатная система. Целесообразно обозначить за начало центральную точку, расположенную в основании заданной геометрической фигуры. Тогда оси ОХ и ОУ будут расположены параллельно относительно сторон этого основания. Вычислим, чему равны координаты точек А, В и С:
\(A\left ( \frac{1}{2};-\frac{1}{2};0 \right )\)
\(B\left ( \frac{1}{2};\frac{1}{2};0 \right )\)
\(C\left ( -\frac{1}{2};\frac{1}{2};0 \right )\)
Так как треугольник AOS имеет прямоугольный угол, справедливо следующее соотношение:
\(OS=\frac{\sqrt{2}}{2}\)
Вершина пирамиды имеет координаты, которые достаточно просто определить:
\(S\left ( 0;0;\frac{\sqrt{2}}{2} \right )\)
Затем с помощью уже известных геометрических закономерностей рассчитаем координаты, соответствующие Е и К:
\(E\left ( \frac{1}{4};\frac{1}{4};\frac{\sqrt{2}}{4} \right )\)
\(K\left ( -\frac{1}{4};\frac{1}{4};\frac{\sqrt{2}}{4} \right )\)
Зная координаты точек, допустимо вычислить координаты направленных отрезков:
\(\overrightarrow{AE}\left ( -\frac{1}{4};\frac{3}{4};\frac{\sqrt{2}}{4} \right )\)
\(\overrightarrow{BK}\left ( -\frac{3}{4};\frac{1}{4};\frac{\sqrt{2}}{4} \right )\)
В результате получим, что косинус угла, который расположен между этими векторами, составляет:
\(cos\varphi =\frac{\overrightarrow{AE}\cdot \overrightarrow{BK}}{\left |\overrightarrow{AE} \right |\cdot \left |\overrightarrow{BK} \right |}=\frac{1}{6}\)
Ответ: \(\frac{1}{6}\)
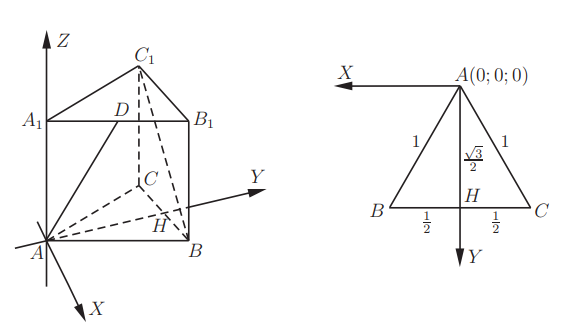
На рисунке изображена геометрическая фигура в виде правильной треугольной призмы. Обозначим ее за ABCA1B1C1. Пусть каждое из ребер этой фигуры составляет единицу. С помощью точки D ребро A1B1 делится пополам. Необходимо вычислить, чему равен косинус угла, сторонами которого являются прямые AD и BC1.
Источник: ege-study.ru
Решение
Предположим, что точка А совпадает с началом координатной системы. Тогда ВС расположена параллельно по отношению к оси абсцисс. Таким образом, ось ординат играет роль перпендикуляра. Отрезок АН принадлежит оси ординат и одновременно является высотой треугольника АВС. Перечислим точки с координатами:
\(A(0;0;0)\)
\(A_{1}(0;0;1)\)
\(B(\frac{1}{2};\frac{\sqrt{3}}{2};0)\)
\(B_{1}(\frac{1}{2};\frac{\sqrt{3}}{2};1)\)
\(C_{1}(-\frac{1}{2};\frac{\sqrt{3}}{2};1)\)
Исходя из того, что точка D делит на две равные части A1B1, запишем следующее:
\(D(\frac{1}{4};\frac{\sqrt{3}}{4};1)\)
Вычислим, чему равны координаты векторов \(\overrightarrow{AD}\) и \(\overrightarrow{BC}_{1}\), что позволит быстро определить угол, сторонами которого эти направленные отрезки являются:
\(\overrightarrow{AD}(\frac{1}{4};\frac{\sqrt{3}}{4};1)\)
\(\overrightarrow{BC_{1}}(-1;0;1)\)
\(cos\varphi =\frac{\overrightarrow{AD}\cdot \overrightarrow{BC_{1}}}{\left |\overrightarrow{AD} \right |\cdot \left |\overrightarrow{BC_{1}} \right |}=\frac{3}{2\sqrt{10}}\)
Ответ: \(\frac{3}{2\sqrt{10}}\)
Задан некий вектор АВ. Требуется идентифицировать координаты этого направленного отрезка, если известно, что он начинается в точке с координатами \(A\left(-1;\; 2\right)\), а заканчивается в точке \(B\left(2;\; -3\right)\).
Решение
Воспользуемся самым простым соотношением, с помощью которого легко вычислить координаты направленного отрезка при известных аналогичных характеристиках его точек:
\(\overline{AB}=\left(2-\left(-1\right)\, ;\; -3-2\right)=\left(3;\; -5\right)\)
Ответ: \(\overline{AB}=\left(3;\; -5\right)\)
Имеется некий вектор с известными координатами, который можно построить на плоскости: \(\overline{AB}=\left(0;\; -4;\; 3\right)\) . Конечная точка этого направленного отрезка имеет координаты: \(B\left(-1;\; 6;\; 1\right)\) . Требуется вычислить, чему соответствуют координаты точки, совпадающей с началом вектора А.
Решение
Предположим, что координаты искомой точки на плоскости соответствуют следующим значениям:
\(A\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\)
В таком случае справедливым является следующее математическое соотношение:
\(\overline{AB}=\left(-1-a_{1} ;\; 6-a_{2} ;\; 1-a_{3} \right)=\left(0;\; -4;\; 3\right)\)
Заметим, что при равенстве пары векторов их координаты также совпадают между собой. В результате можно посчитать координаты таким образом:
\([-1-a_{1} =0\Rightarrow a_{1} =-1\)
\(6-a_{2} =-4\Rightarrow a_{2} =10\)
\(1-a_{3} =3\Rightarrow a_{3} =-2\)
Сформулируем окончательный ответ:
\(A\left(-1;\; 10;\; -2\right)\)
Ответ: \(A\left(-1;\; 10;\; -2\right)\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так