Квадрат суммы и квадрат разности двух выражений
Формула разности квадратов
В процессе изучения тем по алгебре нередко приходится иметь дело с заданиями на различные математические действия с многочленами. Одной из распространенных операций является поиск произведения множителей. В определенных случаях справиться с такими примерами достаточно трудно. На помощь приходят специальные формулы, которые помогают значительно сократить вычисления.
Рациональное решение громоздких задач на умножение заключается в применении справедливых математических закономерностей, в том числе, разности квадратов и квадрата суммы. Далее подробно рассмотрим процедуру выведения указанных соотношений, возможности их практического применения. К примеру, подобный метод расчетов допустимо использовать, когда требуется перемножить многочлены, получить дополнительные множители, найти ответ к задаче, сократить дробные числа, упростить длинные алгебраические записи.
Представим, что имеется пара чисел а и b. Выполним умножение суммы и разности этих чисел. В результате получим следующую цепочку вычислений:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\((a+b)(a-b) = a(a-b)+b(a-b) = a^2-ab+ab-b^2 = a^2-b^2\)
Сформированная запись представляет собой разность квадратов пары выражений, а именно:
\( (a+b)(a-b) = a^2-b^2\)
Произведение суммы и разности пары выражений вычисляется, как разность их квадратов, то есть: \(a^2-b^2 = (a+b)(a-b)\)
Разность квадратов пары выражений представляет собой результат умножения суммы и разности рассматриваемых выражений.
Заметим, что выведенная выше формула универсальна в применении. Допустимо подставлять на место букв а и b какие-либо одночлены или многочлены. Смысл закономерности от таких манипуляций не поменяется. Это позволяет решать по упрощенной схеме практически любые задачи. Рассмотрим типичный пример такого задания.
\((8b^2 c+3k)(8b^2 c-3k) = (8b^2 c)^2-(3k)^2 = 64b^4 c^2-9k^2\)
Если поменять местами исходную запись и результат, то также получим справедливое равенство: \(64b^4 c^2-9k^2 = (8b^2 c)^2-(3k)^2 = (8b^2 c+3k)(8b^2 c-3k)\)
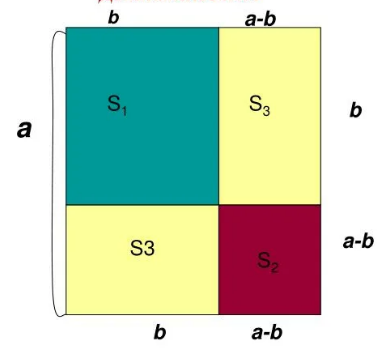
В алгебре нередко выведенные математические закономерности можно объяснить с помощью приемов из курса геометрии. В данном случае для разности квадратов также предусмотрена такая возможность. Представим, что имеется некоторая геометрическая фигура в виде квадрата, одна сторона которого составляет а. В какой-то из его углов вписали квадрат меньшего размера со стороной, равной \(b \lt a\).
Источник: slideserve.com
Площадь рассматриваемой геометрической фигуры складывается из площадей четырехугольников, представленных на изображении выше. В результате получим следующее соотношение:
\(a^2 = (a-b)^2+b^2+2(a-b)b\)
После преобразования записанного равенства получим простую формулу для вычисления разности квадратов пары чисел:
\(a^2-b^2 = (a-b)^2+2b(a-b) = (a-b)(a-b+2b) = (a-b)(a+b).\)
Примеры решения задач
На первый взгляд, задачи с математическими операциями над многочленами сопровождаются массой проблем. Вычисление сложных выражений отнимает много сил и времени. Однако при знании и владениями техниками сокращенного умножения можно существенно ускорить работу над заданиями. В этом случае целесообразно запомнить обозначенные выше закономерности или составить подсказку с ними.
Далее остается лишь действовать по стандартному алгоритму вычисления примеров, начиная с преобразования соотношений к необходимому виду. После применения формулы разности квадратов итоговый результат остается лишь записать в ответ к задаче. Попробуем применить изученный теоретический материал на практике для вычисления нескольких групп типичных примеров.
Дано несколько выражений:
\((x-y)(x+y)\)
\((3-z)(z+3)\)
\((5b+6z)(5b-6z)\)
\(-(2mk-1)(2mk+1)\)
Требуется вычислить результат умножения с помощью рассмотренных ранее математических закономерностей.
Решение
Заметим, что каждое выражение из записанных выше является частью соотношения разности квадратов. Воспользуемся соответствующей формулой и выполним все необходимые преобразования. В результате получим:
\((x-y)(x+y) = x^2-y^2\)
\((3-z)(z+3) = (3-z)(3+z) = 9-z^2\)
\( (5b+6z)(5b-6z) = (5b)^2-(6z)^2 = 25b^2-36z^2\)
\(-(2mk-1)(2mk+1) = -((2mk)^2-1) = 1-4m^2 k^2\)
Ответ: \(x^2-y^2, 9-z^2, 25b^2-36z^2, 1-4m^2 k^2\).
Ниже перечислены выражения на различные математические операции с многочленами:
\((0,7x-11)(0,7x+11)+0,51x^2\)
\(2z^2-(z+1)(z-1)\)
\(15a^2+(-3a-b)(3a-b)\)
\((3a+7b)(7b-3a)+(-2a+5b)(2a+5b)\)
Необходимо вычислить значение этих выражений.
Решение
Как и в предыдущей задаче, здесь целесообразно применить закономерности, позволяющие сократить выражения. Воспользуемся уже знакомой формулой разности квадратов и выполним соответствующие преобразования. В конце останется только записать ответ. В процессе необходимо учитывать, с каким знаком представлены многочлены, чтобы не допустить ошибки при раскрытии скобок.
\((0,7x-11)(0,7x+11)+0,51x^2 = (0,7x)^2-11^2+0,51x^2 = 0,49x^2-121+0,51x^2 = x^2-121\)
\(2z^2-(z+1)(z-1) = 2z^2-(z^2-1) = z^2+1\)
\(15a^2+(-3a-b)(3a-b)=15a^2-(3a+b)(3a-b)=15a^2;(9a^2-b^2)=6a^2+b^2\)
\((3a+7b)(7b-3a)+(-2a+5b)(2a+5b) = (7b+3a)(7b-3a)+(5b-2a)(5b+2a) = (7b)^2-(3a)^2+(5b)^2-(2a)^2 = 49b^2-9a^2+25b^2-4a^2 = 74b^2-13a^2\)
Ответ: \(x^2-121, z^2+1, 6a^2+b^2, 74b^2-13a^2.\)
Дано несколько выражений, записанных в сокращенной форме:
\(25-a^2\)
\(x^2-0,64\)
\(-m^2+49n^2\)
\(c^4 d^2-4k^2\)
Необходимо выделить из представленных записей множители. Разложение нужно выполнить с применением формул сокращенного умножения.
Решение
В данном случае примеры демонстрируют обратную ситуацию, когда исходный вариант записи представляет собой разность квадратов. Если воспроизвести определение этого математического правила наоборот, то получиться разложить записанные выражения на множители. В процессе стоит обратить внимание на знаки в примерах. В некоторых случаях целесообразно переставить компоненты выражения местами, чтобы упростить дальнейшее применение закономерностей и вычисления.
\(25-a^2 = 5^2-a^2 = (5+a)(5-a)\)
\(x^2-0,64 = x^2- 0,8^2 = (x+0,8)(x-0,8)\)
\(-m^2+49n^2 = 49n^2-m^2 = (7n)^2-m^2 = (7n+m)(7n-m)\)
\(c^4 d^2-4k^2 = (c^2 d)^2-(2k)^2 = (c^2 d+2k)(c^2 d-2k)\)
Ответ: \((5+a)(5-a), (x+0,8)(x-0,8), (7n+m)(7n-m), (c^2 d+2k)(c^2 d-2k)\).
Имеется несколько выражений, представленных в формате разности квадратов:
\(58^2-48^2\)
\(132^2-68^2\)
\(0,731^2-0,269^2\)
\((3 \frac{1}{7})^2-(3 \frac{6}{7})^2\)
Требуется найти значение результата математических действий.
Решение
Как и в предыдущих примерах, здесь целесообразно воспользоваться обратным соотношением, описывающим смысл закономерности разности квадратов. Заметим, что примеры состоят не только из целочисленных элементов, но и дробных чисел. По этой причине следует внимательно отнестись к расчетам, правильно определяя число символов после запятой. Применим полученные знания на практике и решим задачи:
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
\(132^2-68^2 = (132+68)(132-68) = 200\cdot64 = 12800\)
\(0,731^2-0,269^2 = (0,731+0,269)(0,731-0,269) = 1\cdot0,462 = 0,462\)
\( (3 \frac{1}{7})^2-(3 \frac{6}{7})^2 = (3 \frac{1}{7}+3 \frac{6}{7})(3 \frac{1}{7}-3 \frac{6}{7}) = 7\cdot(-\frac{5}{7}) = -5\)
Ответ: 1060, 12800, 0,462, -5.
Имеется некоторое математическое выражение, записанное в следующем виде: \((3n+5)^2-16\) Необходимо представить доказательства наличия возможности деления данного многочлена на число 3 при условии, что переменная n принимает разнообразные значения.
Решение
На первый взгляд, задание не является тривиальным. Однако с помощью изученной до этого формулы разности квадратов, можно достаточно компактно записать необходимые доказательства. Действия будут следующие:
\(\frac{(3n+5)^2-16}{3} = \frac{(3n+5)^2-4^2}{3} = \frac{(3n+5-4)(3n+5+4)}{3} = \frac{(3n+1)(3n+9)}{3} = \frac{3(3n+1)(n+3)}{3} = (3n+1)(n+3)\)
Ответ: утверждение доказано.
Квадрат суммы: формулы
Закономерности, руководствуясь которыми можно значительно упростить решение сложных выражений с многочленами, незаменимы при работе с математическими задачами в курсе алгебры в седьмом и последующих классов. Кроме того, сформулированные принципы преобразования записей пригодятся в геометрии, физике и других предметных областях для расчета разнообразных величин. Заметим, что в сформулированные записи допустимо подставлять любые значения, то есть не только буквы а и b, но и разнообразные числа, переменные, самостоятельные выражения.
С целью выведения еще одного справедливого равенства из числа формул сокращенного выражения рассмотрим ситуацию, когда имеется некая сумма (а+b), которую требуется возвести во вторую степень. Выполним поэтапные действия и запишем окончательный результат математических преобразований:
\((a+b)^2 = (a+b)(a+b) = a(a+b)+b(a+b) = a^2+ab+ab+b^2 = a^2+2ab+b^2\)
В итоге несложных вычислений получилось разложить первоначальное выражение на множители. Таким образом, допустимо математически сформулировать формулу квадрата суммы пары выражений:
\((a+b)^2 = a^2+2ab+b^2\)
Квадрат суммы пары выражений вычисляется, как сумма квадрата первого выражения, удвоенного произведения первого и второго выражения и квадрата второго выражения, то есть: \((a+b)^2 = a^2+2ab+b^2\) .
С помощью выведенной закономерности получается существенно сократить расчеты при решении задач на математические операции с одночленами, многочленами, неизвестными, выражениями. В процессе можно избежать необходимости в умножении скобок и последующем приведении подобных путем получения из четырех элементов трех слагаемых. Рассмотрим типичный пример для наглядного представления формулы.
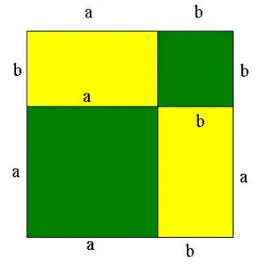
Правило вычисления квадрата суммы можно сформулировать с помощью принципов геометрии. Анализ геометрического доказательства математической закономерности помогает быстро разобраться в принципах вычислений. С этой целью представим на изображении фигуру в виде квадрата, сторона которого соответствует величине а+b.
Источник: slideserve.com
Заметим, что в состав геометрической фигуры входят пара квадратов и пара прямоугольников. Совокупность площадей перечисленных объектов позволяет вычислить общую площадь исходного квадрата. Тогда получим следующее справедливое равенство:
\(S = (a+b)^2 = a^2+b^2+2ab\)
Проанализируем запись. Заметим, что в соотношении скрыта формула квадрата суммы, рассмотренная ранее:
\((a+b)^2 = a^2+2ab+b^2\)
В результате удалось подтвердить корректность закономерности с помощью геометрического обоснования.
В Древней Греции ученый, который специализировался на математических науках, Диофант Александрийский в 3 веке до н.э. решил пренебречь методом записи по канонам геометрии. Труд математика под названием «Арифметика» включал в себя лишь соотношения, где квадраты складывают и вычитают в алгебраическом формате. Известное сегодня символьное представление тождеств появилось, благодаря трудам Виета и Декарта в 16 веке. Обоснование закономерностей авторства Ньютона используется в настоящее время. С другой стороны, положения, сформулированные на границе двух наук, то есть алгебры и геометрии, сохраняют сегодня свою актуальность.
Далее целесообразно рассмотреть еще одну полезную формулу, с помощью которой можно значительно упростить решение задач на разность, возведенную во вторую степень. Воспользуемся прежними обозначениями а и b, чтобы вычислить квадрат от вычитания этих чисел:
\((a-b)^2 = (a-b)(a-b) = a(a-b)-b(a-b) = a^2-ab-ab+b^2 = a^2-2ab+b^2\)
В результате удалось записать закономерность, описывающую принцип возведения в квадрат разности пары каких-либо выражений. Окончательно формула примет следующий вид записи:
\((a-b)^2 = a^2-2ab+b^2\)
Квадрат разности двух выражений вычисляется, как квадрат первого выражения, минус удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.
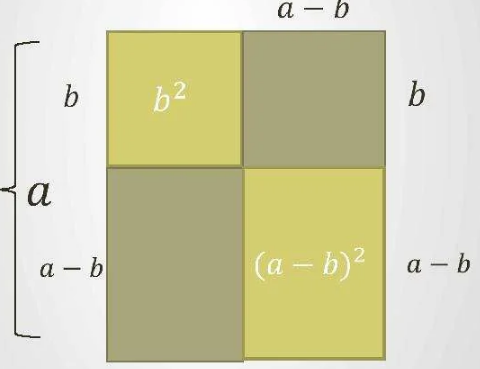
Записанное положение несложно обосновать с точки зрения геометрии. По аналогии с предыдущими доказательствами формул сокращенного умножения в данном случае также целесообразно изобразить квадрат. Пусть сторона этой фигуры равна а. Затем можно вписать в нее квадрат меньшего размера со стороной, составляющей \(b \lt a\).
Источник: mypresentation.ru
Известно, что для расчета площади квадрата нужно лишь возвести во вторую степень его сторону. Применим это правило к нашему примеру и получим:
\(a^2 = (a-b)^2+b^2+2(a-b)b\)
Таким образом:
\((a-b)^2 = a^2-b^2-2(a-b)b = a^2-b^2-2ab+2b^2 = a^2-2ab+b^2\)
Путем нескольких последовательных преобразований получилось доказать справедливость закономерности квадрата разности с помощью принципов геометрии. Это была несложная задача. Однако на практике часто встречаются громоздкие выражения с разными математическими действиями и форматами представления компонентов. Избежать ошибок в процессе работы над ними получится, если соблюдать следующие рекомендации:
- необходимо учитывать наличие второго слагаемого в выражениях квадрата двучленов;
- важно правильно расставлять знак плюса и минуса перед слагаемыми;
В качестве наглядных примеров рассмотрим некорректную и правильную запись вычислений. В первом случае в расчетах допущены ошибки: \((a+b)^2\neq a^2+b^2\) или \((a-b)^2 \neq a^2-b^2\)
Вторая запись является верной: \((a+b)^2 = a^2+ 2ab+b^2\) и \((a-b)^2 = a^2 -2ab+ b^2\)
Интересный исторический факт заключается в том, что формулы для упрощенного умножения чисел и выражений применялись еще в древние времена, то есть за много столетий до нашей эры. Однако при этом математики пользовались геометрическими принципами записи алгебраических закономерностей и положений. К примеру, в Древней Греции было принято использовать прямые отрезки для обозначения той или иной величины. Таким образом, сформировалось целое направление на границе двух наук, названное «геометрическая алгебра».
Задачи
Ниже записано несколько типичных выражений с квадратом суммы:
\((x+y)^2\)
\((3+t)^2\)
\((3a+4b)^2\)
\((4k^2 m+5n)^2\)
Нужно вычислить, чему равны значения этих выражений.
Решение
Воспользуемся формулой для расчета квадрата суммы, которая была изучена в теоретическом курсе. При этом потребуется проанализировать запись и раскрыть соответствующим образом скобки. Выполним необходимые действия и сформулируем ответ:
\((x+y)^2 = x^2+2xy+y^2\)
\((3+t)^2 = 3^2+2\cdot3t+t^2 = 9+6t+t^2\)
\((3a+4b)^2 = (3a)^2+2\cdot3a\cdot4b+(4b)^2 = 9a^2+24ab+16b^2\)
\((4k^2 m+5n)^2 = (4k^2 m)^2+2\cdot4k^2 m\cdot5n+(5n)^2 = 16k^4 m^2+40k^2 mn+25n^2\)
Ответ:\(x^2+2xy+y^2, 9+6t+t^2, 9a^2+24ab+16b^2, 16k^4 m^2+40k^2 mn+25n^2.\)
Дано несколько выражений, результат решения которых нужно записать с помощью закономерности, определяющей квадрат разности:
\((m-n)^2\)
\((x-5)^2\)
\((7y-9z)^2\)
\((3km^2-8n^2 )^2\)
Решение
На первый взгляд задача по уровню сложности не отличается от первого примера. Можно быстро записать ответ, применяя к каждому указанному выше выражению формулу квадрата разности. Однако в этом случае также пригодится подсказка с моментами в расчетах, на которые требуется обратить внимание. К примеру, важно правильно выполнить расстановку знаков. Учитывая все нюансы, воспользуемся соответствующей формулой и запишем ответ:
\((m-n)^2 = m^2-2mn+n^2\)
\((x-5)^2 = x^2-2x\cdot5+5^2 = x^2-10x+25\)
\((7y-9z)^2 = (7y)^2-2\cdot7y\cdot9z+(9z)^2 = 49y^2-126yz+81z^2\)
\((3km^2-8n^2 )^2 = (3km^2 )^2-2\cdot3km^2\cdot8n^2+(8n^2 )^2 = 9k^2 m^4-48km^2 n^2+64n^4\)
Ответ: \(m^2-2mn+n^2, x^2-10x+25, 49y^2-126yz+81z^2, 9k^2 m^4-48km^2 n^2+64n^4.\)
Требуется вычислить значения следующих выражений:
\((10m-1)^2+20m\)
\(36k^2-(1-6k)^2\)
\(4(x-1)-(2x+1)^2\)
\(\frac{1}{3} (3y+4)^2-8y\)
Решение
С помощью формул сокращенного умножения избавимся от скобок и выполним соответствующие математические преобразования:
\((10m-1)^2+20m = (10m)^2-2\cdot10m\cdot1+1+20m = 100m^2-20m+1+20m = 100m^2+1\)
\(36k^2-(1-6k)^2 = 36k^2-(1-2\cdot6k+(6k)^2 ) = 36k^2-1+12k-36k^2 = 12k-1\)
\(4(x-1)-(2x+1)^2 = 4x-4-((2x)^2+2\cdot2x+1) = 4x-4-4x^2-4x-1 = -4x^2-5\)
\(\frac{1}{3} (3y+4)^2-8y = \frac{1}{3} ((3y)^2+2\cdot3y\cdot4+4^2 )-8y = \frac{1}{3} (9y^2+24y+16)-8y=3y^2+8y+\frac{16}{3}-8y=3y^2+5 \frac{1}{3}\)
В результате получились достаточно компактные записи, которые можно представить в виде ответа.
Ответ: \(100m^2+1, 12k-1, -4x^2-5, 3y^2+5 \frac{1}{3}.\)
Дано несколько уравнений:
\((7-x)^2-(x+8)^2 = 45\)
\((2x-15)^2-x(4x+3) = 153\)
С помощью формул сокращенного умножения нужно вычислить значения переменных, которые входят в состав записанных выше равенств.
Решение:
\((7-x)^2-(x+8)^2 = 45\)
\(49-14x+x^2-(x^2+16x+64) = 45 <p>49-14x-16x-64 = 45</p>\)
-30x = 45-49+64
-30x = 60
x = -2
\((2x-15)^2-x(4x+3) = 153\)
\((2x)^2-2\cdot2x\cdot15+15^2-4x^2-12x = 153\)
-60x+225-12x = 153
-72x = 153-225
-72x = -72
x = 1
Ответ: -2; 1.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так