Как найти касательную к окружности
Касательная к окружности — это
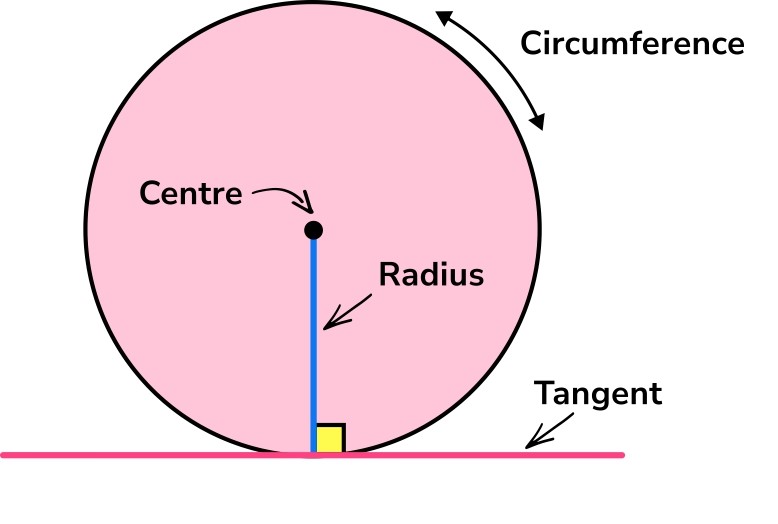
Линия, касающаяся окружности в одной точке, называется касательной к окружности. В одной точке окружности может быть только одна касательная. Ее можно рассматривать для любых изогнутых фигур.
Если расстояние между центром окружности и прямой равно радиусу окружности, то данная прямая будет касаться окружности.
Существует ровно две касательные к окружности из точки вне окружности. Мы можем провести только одну касательную к окружности через точку, лежащую на окружности. Касательная не может быть проведена из точки, лежащей внутри окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угол между касательной и радиусом равен 90 градусам. Касательные, пересекающиеся в одной точке, имеют равную длину.
Источник: thirdspacelearning.com
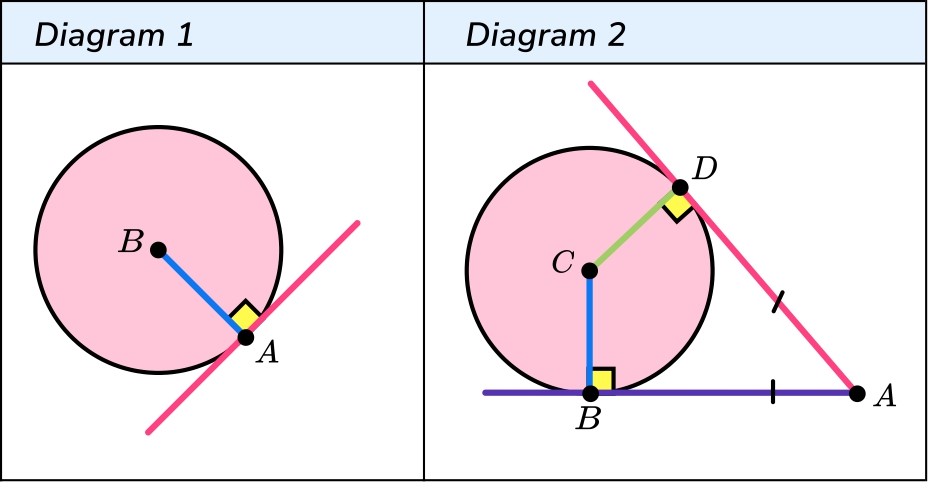
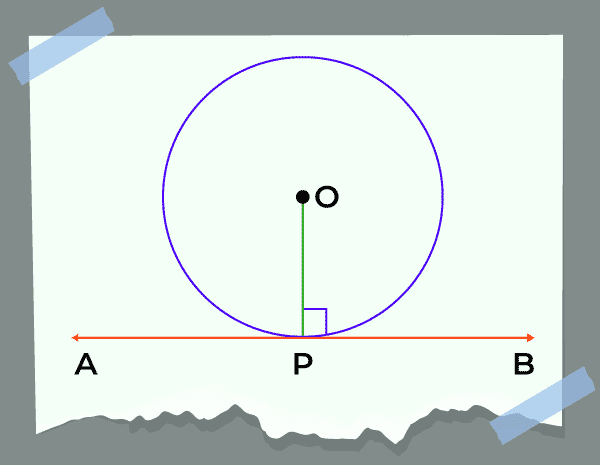
На диаграмме 1 касательная пересекает окружность в точке A, которая перпендикулярна (90 градусов к) радиусу окружности в этой точке (точка касания находится в точке A).
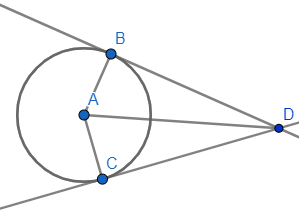
На диаграмме 2 две касательные пересекают окружность в двух разных точках (B и
D) и пересекаются в точке A. Если точки B и D соединены хордой, AB и AD имеют одинаковую длину, поэтому ABD — равнобедренный треугольник. Если точки B и D соединяются с центром окружности C, они образуют воздушного змея ABCD.
Свойства
- Это линия, которая никогда не входит во внутреннюю часть окружности.
- Касается кривой только в одной точке.
- Касается радиуса окружности в точке касания под прямым углом.
- Помимо перечисленных свойств, касательная к окружности имеет математические теоремы, которые используются при выполнении основных вычислений в геометрии.
Если частица или объект движется по круговой траектории, а мы резко останавливаем его движение, то он будет двигаться в направлении, касательном к круговой траектории. То есть направление скорости будет касательным к круговой траектории.
Окружность и касательная к окружности могут применяться в нашей повседневной жизни, например, в строительстве, архитектуре и машиностроении.
Пример из реальной жизни: Когда колеса велосипеда катятся по дороге, линию дороги можно сравнить с касательной к колесу в каждой точке.
Теорема
Теорема 1: о радиусе касательной
Касательная составляет прямой угол с радиусом окружности в точке касания.
(В точке касания касательная перпендикулярна радиусу).
Источник: thirdspacelearning.com
Доказать: Радиус OP перпендикулярен касательной AB.
Доказательство:
Точки A и B лежат вне окружности.
Таким образом, мы можем написать:
OA > OP
OB > OP
Таким образом, для любой такой точки на прямой AB мы получим то же самое соотношение.
Это означает, что OP — кратчайшее расстояние между прямой AB и точкой O.
Таким образом, OP⊥AB
∠OPA = ∠OPB = 90°.
Теорема 2: о двух касательных
Длины двух касательных, проведенных из общей внешней точки к окружности, равны. Эти две касательные образуют равные углы в центре. Прямая, соединяющая внешнюю точку с центром, разделит угол между касательными на два равных угла.
Источник: thirdspacelearning.com
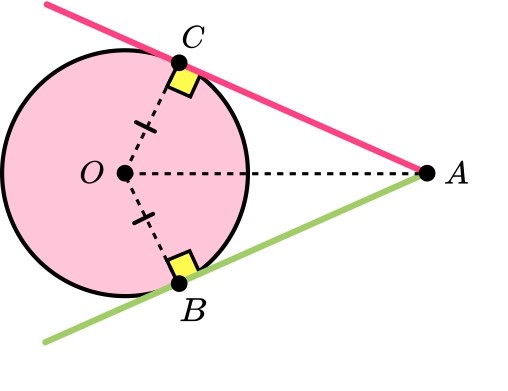
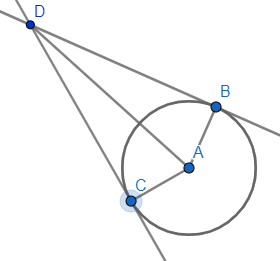
Рассмотрим две касательные линии AC и AB, проведенные из внешней точки A, как показано на рисунке, тогда:
AC = AB
Две касательные к центру окружности образуют равные углы. ∠AOC = ∠AOB
Линия, соединяющая внешнюю точку с центром, разделит угол между касательными на два равных угла. ∠OAC = ∠OAB
Построение
-
Шаг 1: Нарисуйте окружность нужного радиуса с центром O.
-
Шаг 2: Соедините O и любую точку P на окружности. OP — радиус.
-
Шаг 3: Проведите линию, перпендикулярную радиусу OP, через точку P. Эта линия будет касательной к окружности в точке P.
Вне окружности:
- Шаг 1: Рассмотрим точку A вне окружности с центром O.
- Шаг 2: Соедините точки A и O, проведите биссектрису AO. Пусть P — средняя точка AO.
- Шаг 3: Начертите окружность с центром P и радиусом PO. Эта окружность пересечется в двух точках B и C на окружности с центром O.
- Шаг 4: Соедините точку A с B и C.
Как найти: формула
Рассмотрим окружность с P — любой внешней точкой, PQ — касательная, а AB — секущая, проведенная из внешней точки P.
Здесь PA — отрезок внешней секущей.
Формула для отношения касательной к секущей имеет вид:
PQ2 = PA x PB.
Общее уравнение
Если уравнение окружности имеет вид x2 +y2 = r2, а из любой внешней точки (a, b) проведена касательная, то общее уравнение касательной к окружности имеет вид:
xa + yb = r2.
Если общее уравнение прямой равно y=mx+c, а уравнение окружности равно x2 +y2 = r2, тогда общее уравнение касательной к окружности: y = mx ± r√1+m2.
Уравнение касательной к окружности x2 +y2 = a2 в точке (a cos θ, a sin θ ) это x cos θ+y sin θ= a.
Касательная к уравнению окружности x2+ y2+2gx+2fy+c =0 at (x1, y1) is xx1+yy1+g(x+x1)+f(y +y1)+c =0.
Примеры решения задач
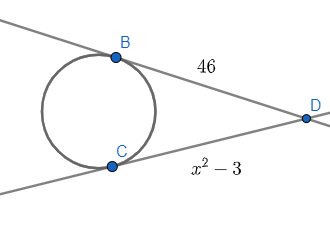
На рисунке ниже длина отрезка BD равна длине отрезка CD. Определите значение x.
Источник: study.com
Определите, какой длины не хватает на рисунке. Глядя на рисунок, мы знаем, что длина BD равна 46 единицам. Длина CD равна x2 - 3 единиц. Мы знаем, что длина BD равна длине CD, поэтому CD должен быть равен 46 единицам. Это означает, что мы можем установить x2 - 3 равным 46 и решить для x.
Так как BD и CD имеют равные длины, мы можем поставить их равными друг другу и решить для x:
x2 - 3 = 46
Прибавьте 3 с обеих сторон.
x2 = 49
Возьмите квадратный корень из обеих сторон.
x = 7
Итак, длина CD равна 46 единицам при x = 7.
AB — касательная к окружности с центром O в точке A радиуса 6 см. Она пересекает прямую OB так, что OB = 10 см. Чему равна длина AB?
Мы знаем, что AB является касательной к окружности в точке A.
Поскольку касательная AB перпендикулярна радиусу OA,
ΔOAB - прямоугольный треугольник, а OB - гипотенуза ΔOAB.
Используя теорему Пифагора:
OB2 = OA2 + AB2
AB2 = √OB2 - √OA2
AB = OB2 - OA2 = √102 - √62 = √64 = 8 см.
Длина AB равна 8 см.
На рисунке ниже AC = 8 см, а BD = 15 см. Найдите длину AD.
Источник: study.com
Определим, какой длины не хватает. Рассматривая рисунок, можно выделить два треугольника: треугольник ABD и треугольник ACD. Согласно теореме о двух касательных, эти треугольники имеют одинаковые длины. Сказано, что AD не хватает, поэтому ищем именно его.
Найдем недостающую длину. Чтобы найти AD, применим теорему Пифагора к треугольнику ACD. В этом треугольнике AC и CD — ноги, поэтому AD — гипотенуза. Таким образом, мы оцениваем c в теореме Пифагора: 82 + 152 = c2.
64 + 225 = c2
289 = c2
c = 17
Таким образом, длина AD составляет 17 см.
Если PQ и PR — две касательные к окружности с центром O, такие, что ∠POQ = 110°, то найдите значение ∠RPQ.
Дано:
PQ и PR - касательные к окружности с центром O.
Мы знаем, что радиус перпендикулярен касательной к окружности.
Таким образом, OQ перпендикулярен PQ, а OR перпендикулярен PR.
∠OQP = 90°
⇒ ∠ORP = 90°
Используя свойство суммы углов четырехугольников.
∠RPQ + ∠QOR + ∠OQP + ∠ORP = 360°
⇒ ∠RPQ = 360° - (110° + 90° + 90°)
⇒ ∠RPQ = 70°
Таким образом, значение ∠RPQ равно 70°.
Найдите длину ножек, учитывая радиус и гипотенузу На рисунке ниже AD = 25 см, а радиус окружности равен 7 см. Найдите длины отрезков AB и CD.
Источник: study.com
Не хватает двух отрезков — AB и CD. Теорема о двух касательных подтверждает, что AB = AC и CD = BD и что треугольники ABD и ACD конгруэнтны. Итак, нам нужно найти длины ножек.
Найдем недостающие длины. Радиус равен 7 см, это расстояние от центра окружности до самой окружности. Поэтому длина AB = 7 см. Теперь мы можем использовать теорему Пифагора, чтобы найти длину CD, которую мы назовем b:
72 + b2 = 252
Возведите в квадрат 7 и 25.
49 + b2 = 625
Вычтите 49 с обеих сторон.
b2 = 576
Возьмите квадратный корень из обеих сторон.
b= 24
Итак, длина AB = 7 см, а длина CD = 24 см.
Радиус окружности = 5 см. Найдите длину касательной AB, если OP дано равным 13 см.
Источник: geeksforgeeks.org
Дано:
AB — касательная к окружности в точке O.
Известно, что касательная AB перпендикулярна радиусу OP,
В прямоугольном треугольнике ΔOPB с помощью теоремы Пифагора,
OP2 + PB2 = OB2
⇒ PB2 + 52 = 132
⇒ PB2 = 169 - 25 = 144
⇒ PB = √(144) = 12 см
Длина касательной AB = 2×PB = 2×12 = 24 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так