Действия со степенями: формулы и примеры

Степень числа — это

В математике предусмотрены разные операции для чисел, величин, функций. В задачах нередко можно встретить примеры, где некоторое значение необходимо возвести в определенную степень. Подобные действия обладают рядом особенностей и свойств, которые важно учитывать для упрощения вычислений и исключения ошибок в расчетах. Начать изучение темы стоит с введения ключевого понятия.

Составные элементы степени произвольного числового значения:

• основание;
• показатель.

Показатель степени выбирают из какого-либо числового множества:

• натуральные числа;
• целые числа;
• рациональные числа.

При обозначении степени используют специальную запись. К примеру, в \(2^3\) основание равно 2 и возводится в степень, соответствующую 3. По итогам вычисления степени получают отличное от первоначального значение, рассчитанное путем умножения основания на себя такое количество раз, которое отмечено в показателе.

Свойства степеней

Рассмотрим свойства, характерные для степеней с натуральным показателем:

• произведение числового значения на себя в течение нескольких раз дает результат в виде степени с показателем, равным суммированию показателей, то есть: \(a^m \cdot a^n = a^{(m + n)};\)
• частное пары степеней, которые записаны с идентичными основаниями, соответствует степени с показателем, вычисляемым с помощью вычитания показателей: \(\frac{a^m}{a^n}= a^{(m – n)};\)
• в процессе возведения степени в степень с равными основаниями получают степень, показатель которой соответствует результату умножения показателей, то есть: \((a^m)^n = a^{(m – n)};\)
• если умножить степень на произведение с идентичным снованием, то получится произведение степеней, которые содержат показатель, вычисляемый как произведение показателей: \(a^m \cdot b^m = (a \cdot b)^m;\)
• частное от деления степени на произведение при равных значениях снования дает в итоге частное степеней с показателем, рассчитанным при вычитании показателей, то есть: \(\frac{a^m}{b^m}= (\frac{a}{b})^m.\)

В случае степеней, которые обладают целым показателем, предусмотрено несколько специфических особенностей:

• результатом возведения численного значения в нулевую степень является 1, например, \(a^0 = 1\);
• если возвести число в степень со знаком минуса, то итогом расчетов станет обратное число, возведенное в положительную степень, то есть:\(a^{-n}= \frac{1}{a^n}\) .

В заданиях повышенного уровня сложности встречаются примеры вычисления степеней с рациональными показателями. Упростить подобные расчеты удобно с помощью характерных для данного типа степенных выражений свойств:

• \(a^{\frac{m}{n}} = \sqrt{(a^m)^n}\);
• \(a^{\frac{m}{n}} = (n\sqrt{a})^m\).

Действия со степенями

Со степенями производят различные математические действия. При выполнении расчетов необходимо учитывать принципы и правила вычислений. Рассмотрим основные виды действий. Если степени обладают идентичными основаниями, то произведение таких степеней вычисляют путем сложения показателей и записи основания без изменений, то есть:

\(a^n \cdot a^m=a^{n+m}\)

Найти частное от деления степеней, обладающих не отличающимися основаниями, допустимо с помощью записи аналогичного основания и вычитания показателей по формуле:

\(\frac{a^n}{a^m}=a^{n-m}\)

Степень можно возводить в какую-либо степень. При этом необходимо переписать основание без изменений и выполнить умножение исходных показателей. Озвученное действие удобно представить в виде математического соотношения:

\((a^n)^m = а^{n\cdot m}\)

Произведение с определенными множителями также допустимо возвести в степень. В процессе вычислений данного выражения потребуется последовательно возвести в заданную степень каждый из множителей, то есть:

\((a\cdot b\cdot c)^m=a^m\cdot b^m\cdot c^m\)

При вычислении степени частного или дробного числа, нужно выполнить возведение в имеющуюся степень числителя и знаменателя с помощью универсальной формулы:

\((\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}}\)

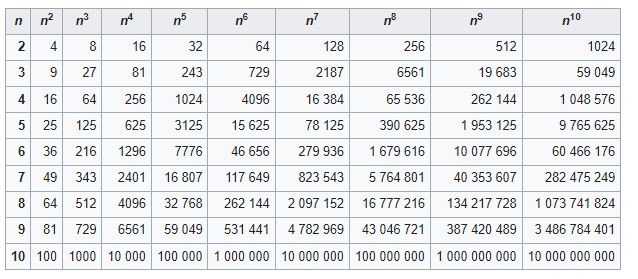
Таблица

При выполнении заданий на возведение в степень небольших числовых значений допустимо воспользоваться табличной формой, где представлены соответствующие результаты расчетов:

 

Источник: ru.wikipedia.org.

Примеры решения задач

Решение

На первом шаге необходимо проанализировать заданное выражение. Заметим, что в числителе и знаменателе дроби записаны степени. Удобно привести степени над дробной чертой к одному основанию. С этой целью выполним соответствующие преобразования:

\(8^{-2} = {(2^3)}^{-2} = 2^{-6}\)

После несложных математических действий удалось представить начальное выражение в формате, подходящим для дальнейших вычислений:

\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}} = \frac{2^{2} \cdot 2^{-6}}{2^{-5}} = 2^{2-6-(-5)} = 2^{1} = 2\)

Ответ: 2.

Решение

Заметим, что числовой множитель, равный 27, допустимо представить в виде степени, а именно:

\(27 = 3^3\)

В результате удалось преобразовать исходное выражение в умножение степеней, которые не отличаются по основаниям. Воспользуемся правилом вычисления произведения подобных значений, что подразумевает запись основания без изменений и сложение показателей. Выполним соответствующие расчеты и запишем окончательный ответ:

\(27 \cdot 3^n = 3^3 \cdot 3^n = 3^{n+1}\)

Ответ: \(3^{n+1}.\)

Решение

По аналогии с предыдущими примерами начнем вычисления с анализа представленной записи. Заметим, что степени за исключением одной содержат основания, равные 5. Привести все степени к одинаковому основанию несложно путем следующих преобразований:

\(25^{3} = {(5^2)}^{3} = 5^{6}\)

Далее воспользуемся правилом деления и умножения степеней. В результате последующих вычислений основание остается без изменений, а необходимые действия сложения и вычитания нужно выполнить с показателями. Запишем соответствующие процедуры и сформулируем окончательный ответ:

\(\frac{5^{6}}{25^{3}\cdot 5^{-2}} = \frac{5^{6}}{5^{6}\cdot 5^{-2}} = 5^{6-6-(-2)}=5^2=25\)

Ответ: 25.