Формулы приведения в тригонометрии

Формулы приведения — это

Тригонометрические функции представляют собой простейшие выражения, сформулированные в результате изучения треугольных геометрических фигур с прямыми углами. С помощью основных закономерных уравнений выявлена взаимосвязь между размерами сторон рассматриваемых треугольников и острых углов, расположенных при гипотенузе. Такие соотношения в дальнейшем стали применяться в разных научных сферах. В течение длительного временного периода развития математических знаний и геометрии удалось расширить понятие тригонометрических функций. Например, в настоящее время в качестве аргумента функции принимают какое-либо число из множества вещественных и комплексных числовых значений.

Перечислим прямые и производные функции тригонометрии, которые часто можно встретить в задачах:

• синус \((\sin x)\);
• косинус \((\cos x)\);
• тангенс \(\left(\mathrm {tg} \, x={\frac {\sin x}{\cos x}}\right)\);
• котангенс \(\left(\mathrm {ctg} \, x={\frac {\cos x}{\sin x}}\right)\);
• секанс \(\displaystyle \left(\sec x={\frac {1}{\cos x}}\right)\);
• косеканс \(\displaystyle \left(\mathrm {cosec} \, x={\frac {1}{\sin x}}\right)\).

Важно отметить, что в начале записи функции требуется поставить знак, соответствующий начальной функции в рассматриваемой четвертой части координатной плоскости, соблюдая условие, когда угол \alpha меньше 90^\circ. Несколько типичных примеров таких выражений:

\(\cos \left(\frac{\pi}{2} - \alpha \right) = \sin \alpha\)

\(\cos \left ( 90^\circ - \alpha \right) = \sin \alpha\)

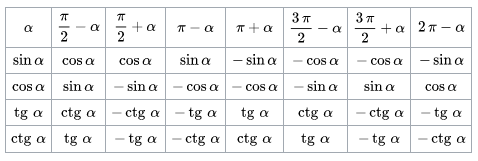
Распространенные для практического применения формулы приведения:

 

Источник: ru.wikipedia.org

Синус

Разбор функции приведения с синусом стоит начать с формул, применимых к суммированию синуса и косинуса. Запишем соответствующие соотношения:

\(\sin \left(\alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta\)

\(\sin \left(\alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta\)

\(\cos \left(\alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta\)

Воспроизведем уравнение приведения для синуса:

\(\sin (\dfrac {\pi}{2} + \alpha) = \cos \alpha\)

Попробуем представить доказательства справедливости представленного равенства. Воспользуемся формулой для определения синуса суммы, заменив таким способом фрагмент формулы слева:

\(\sin (\dfrac {\pi}{2} + \alpha)=\sin \dfrac {\pi}{2} \cdot \cos \alpha + \sin \alpha \cdot \cos \dfrac {\pi}{2}\)

Выполним дальнейшие вычисления и преобразуем записанное выражение:

\(\sin \dfrac {\pi}{2}\)

\(\cos \dfrac {\pi}{2}\)

\(1 \cdot \cos \alpha + \sin \alpha \cdot 0 = \cos \alpha\)

\(\sin (\dfrac {\pi}{2} + \alpha) = \cos \alpha\)

В результате путем несложных математических манипуляций удалось доказать соответствие действительности формулы приведения для синуса.

Косинус

По аналогичному алгоритму действий представим доказательства практической применимости и обоснованности формулы приведения для косинуса, которая имеет следующий вид:

\(\cos(\pi + \alpha)=-\cos \alpha\)

Преобразуем составной компонент уравнения, расположенный в левой части, используя определение для косинуса суммы:

\(\cos(\pi + \alpha) = cos \pi \cdot cos \alpha - sin \pi \cdot sin \alpha\)

Проведем несколько простых вычислений:

\(cos \pi \cdot cos \alpha - sin \pi \cdot sin \alpha = -1 \cdot cos \alpha - 0 \cdot sin \alpha = - cos \alpha\)

Исходя из полученного равенства, можно записать сокращенное выражение, доказывающее справедливость уравнения приведения для косинуса:

\( \cos(\pi + \alpha)=-\cos \alpha\)

Тангенс

С целью доказательства формулы приведения для такой тригонометрической функции, как тангенс, необходимо в первую очередь обратиться к ее определению. Под тангенсом понимают отношение синуса к косинусу. С учетом сформулированного утверждения подтверждение справедливости уравнения приведения сводится к нетривиальным математическим вычислениям:

\(\tan(\pi - \alpha)=\dfrac{\sin (\pi - \alpha)}{\cos (\pi - \alpha)}= \dfrac{\sin \pi \cdot \cos \alpha - \sin \alpha \cdot \cos \pi}{cos \pi \cdot cos \alpha + sin \pi \cdot sin \alpha} = \dfrac{0 \cdot \cos \alpha - \sin \alpha \cdot (-1)}{(-1) \cdot cos \alpha + 0 \cdot sin \alpha} = \dfrac{\sin \alpha}{-\cos \alpha} = -\tan \alpha\)

Котангенс

Формулу приведения для котангенса записывают в следующем виде:

\(\left(\mathrm {ctg} \, x={\frac {\cos x}{\sin x}}\right)\)

Доказательство справедливости записанного выше соотношения тригонометрических величин аналогично вычислениям для тангенса. Предусмотрен общий алгоритм выведения изучаемых выражений:

• записать аргумент функции в формате \( (\dfrac {\pi n}{2} \pm \alpha)\) , где n обозначает числовое значение из множества целых чисел, угол \alpha меньше, чем \(90^\circ\), то есть находится на интервале \( \left [0; \dfrac{\pi}{2} \right ]\);
• отметить на единичном круге рассматриваемый угол;
• используя построенную окружность, выяснить, какой знак характерен для исследуемой функции, с целью его записи перед функцией, расположенной справа в выражении;
• когда в аргументе у опорной отметки \(\dfrac {\pi n}{2}\) не является четным, то начальную функциональную запись следует изменить на кофункцию;
• обратная ситуация свидетельствует об отсутствии необходимости в замене функции.

В результате формулы приведения функций в тригонометрии представляют собой тождественные выражения:

\(f(\dfrac{\pi n}{2} \pm \alpha)=\Bigg\lbrace\begin{matrix}\pm f(\alpha) \text{, если n четное} \\ \pm co f(\alpha) \text{, если n нечетное}\end{matrix}\)

Примеры решения задач

Решение

Начать вычисление примера следует с анализа записанных угловых мер. Заметим, что в сумме 41 и 49 составляют 90, то есть получается прямой угол. Данного вывода достаточно, чтобы преобразовать запись функции таким способом:

\(41^\circ + 49 ^\circ = 90^\circ\)

\(\cos 41^\circ = \cos (90^\circ - 49^\circ)\)

Сформулированное выражение позволяет применить ранее изученные формулы приведения. После небольшой корректировки начальной записи целесообразно приступить к следующему этапу работы с окружностью. Косинус в первой четвертой доле плоскости, ограниченной кругом, характеризуется знаком плюса. Опорная точка прямого угла расположена на оси по вертикали, что допускает применение соответствующего правила и замену косинуса функцией синуса. В результате получим, что:

\(\cos (90^\circ - 49^\circ) = \sin 49^\circ\)

По итогам выполнения логичных преобразований сформулируем выражение для окончательного расчета и путем его упрощения вычислим искомый ответ:

\(\dfrac{45 \cos {{41}^\circ}}{\sin⁡{{49}^\circ}} = \dfrac{45 \cos (90^\circ - 49^\circ)}{\sin⁡{{49}^\circ}}=\dfrac{45 \sin 49^\circ}{\sin 49^\circ}=45\)

Ответ: 45.

Решение

Заметим, что в данном случае целесообразно воспользоваться формулами приведения. Подставим нужные выражения, известные из теоретического материала, в исходную запись. Далее по стандартному алгоритму действий остается выполнить необходимые математические преобразования и записать окончательный ответ:

\(\frac{1 - \cos 200^\circ}{1 + \sin 70^\circ} = \frac{1 - \cos (180^\circ + 20^\circ)}{1 + \sin (90^\circ - 20^\circ)} = \frac{1 – (- \cos 20^\circ)}{1 + \cos 20^\circ} = \frac{1 + \cos 20^\circ}{1 + \cos 20^\circ} = 1\)

Ответ: 1.