Основные формулы окружности
Что такое окружность
Простейшей кривой считают окружность. Упоминания об этой геометрической фигуре сохранились с давних времен. К примеру, в трудах Аристотеля рассматривались астрономические тела, перемещающиеся по кругу. Подобные умозаключения выдвигали и другие ученые. Однако в 17 веке теорию удалось упразднить, благодаря исследованиям Коперника, Галилея, Кеплера, Ньютона.
С окружностью и ее характеристиками часто сталкиваются учащиеся еще в средних классах школы. В процессе изучения темы они решают разнообразные задачи по геометрии. Кроме того, в физике распространено такое явление, как движение материальной точки и тела по окружности под влиянием каких-либо внешних и внутренних сил разной природы. В связи с этим, полезно ознакомиться с ключевыми соотношениями и формулировками, характерными для понятия окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: ru.wikipedia.org
Окружность представляет собой комплекс точек, размещенных в рамках определенной плоскости, равноудаленных от некоторой центральной точки.
За единичную окружность принимают геометрическую фигуру в виде окружности с радиусом, соответствующим 1.
Круг является фрагментом некоторой плоскости, границы которого имеют вид окружности.
При поиске ответов на различные вопросы, касаемо расположения и размеров окружности, как правило, оперируют понятиями ее радиуса и диаметра. Рассмотрим подробнее эти обозначения, чтобы понимать смысл применения формул.
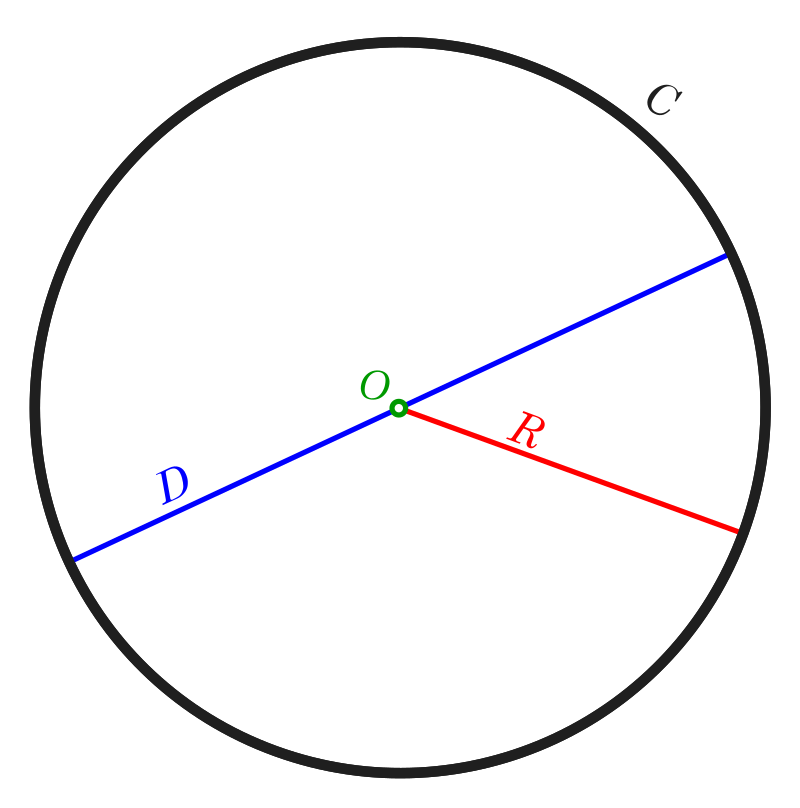
Радиусом окружности, который обозначают за R, называют длину отрезка, один конец которого совпадает с центром фигуры, а второй — является какой-либо точкой, расположенной на рассматриваемой окружности.
Диаметр окружности, для обозначения которого часто используют букву D, представляет собой отрезок, пересекающий центральную точку этой геометрической фигуры и соединяющих две точки, расположенные на окружности.
Во времена Древней Греции окружность имела статус совершенной геометрической фигуры. Дело в том, что с точки зрения любой из точек, принадлежащих окружности, она является однотипной. Таким образом, круг обладает способностью к самостоятельному движению. Исходя из уникального свойства окружности, человек изобрел колесо.
Свойства
Решение различных примеров по геометрии, когда требуется вычислить характеристики окружности, значительно упрощается, если знать свойства этой фигуры. Также описанные ниже закономерности и соотношения полезно использовать в процессе вычислений физических величин. Перечислим свойства, которыми обладает абсолютно любая окружность:
- С целью вычисления диаметра какой-либо окружности необходимо в два раза увеличить ее радиус, то есть: \(D = 2 \cdot r\)
- Минимальный путь от центральной точки окружности до секущей линии, называемой хордой, в любом случае меньше по сравнению с радиусом этой фигуры.
- С помощью 3 точек, расположенных на разных прямых, допустимо построить единственную окружность.
- Если сравнить между собой кривые линии, которые замкнуты и сопоставимы по протяженности, то окружность имеет среди них максимальную площадь.
- При соприкосновении пары окружностей в какой-то точке, она будет расположена на прямой, которая пересекает центральные точки рассматриваемых геометрических фигур.
Формулы, связанные с окружностью
Длину окружности можно вычислить, если известна величина ее диаметра, то есть:
\(L = π \cdot D\)
Существует другое справедливое равенство, которое также подходит для определения длины окружности:
\(L = 2 \cdot π \cdot r\)
Запишем пару полезных уравнений, которые целесообразно использовать при необходимости вычисления площади круга:
\(S = π \cdot r^{2}\)
\(S = π \cdot \frac{D^{2}}{4}\)
В процессе решения задач нередко встречаются геометрические фигуры, рассматриваемые в рамках некой координатной плоскости. Если подразумевается декартовая система координат, то справедливо составить следующее соотношение для окружности, которая имеет радиус, равный r, а ее центральная точка совпадает с началом этой системы:
\(r^{2} = x^{2} + y^{2}\)
Представим несколько иную ситуацию, когда центр геометрической фигуры в виде окружности совпадает с какой-либо точкой, координаты которой равны (a, b). Тогда целесообразно видоизменить предыдущее равенство:
\(r^{2} = (x - a)^{2} + (y - b)^{2}\)
Если учащемуся попалась задача по геометрии на тему окружности «со звездочкой», то может пригодиться параметрическое соотношение:
\(\begin{cases} & x = a + r cos t \\ & y = b + r sin t\end{cases}\)
Объекты разного происхождения круглой формы с давних времени вызывали у людей интерес. Например, бревна круглого сечения использовали древнеегипетские строители при возведении грандиозных по своему масштабу пирамид. С их помощью можно достаточно быстро транспортировать тяжести и строительные материалы.
Задачи
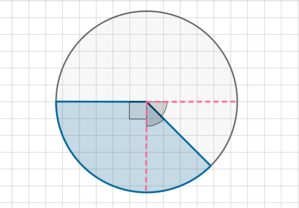
На тетрадном листе изображена окружность, ограничивающая некую плоскость. В результате образован круг, площадь которого составляет 2,8. Требуется вычислить величину площади заштрихованной области.
Источник: shkolkovo.net
Решение
Фрагмент плоскости в цвете включает в себя пару областей, которые не имеют общих точек пересечения и равны \(\frac14 и \frac12 от \frac14\) рассматриваемой окружности:
В результате, можно вычислить искомую величину площади:
\(\dfrac14S+\dfrac12\cdot \left(\dfrac14S\right)=\dfrac38S=\dfrac38\cdot 2,8=1,05.\)
Ответ: 1,05.
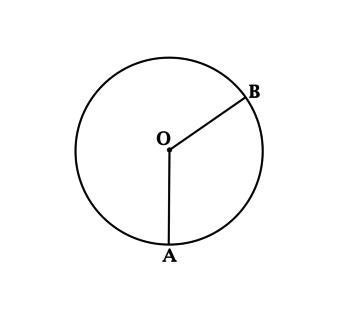
Протяженность кривой в виде окружности составляет 12. Ее центр обозначили за О. Угол \(\angle AOB\) равен \(120^{\circ}\), точки A и B принадлежат рассматриваемой окружности и делят ее пополам. Требуется вычислить, во сколько раз протяженность максимальной из образованных дуг больше, чем минимальная дуга.
Источник: shkolkovo.net
Решение
Заметим, что соотношение протяженностей дуг соответствует отношению их градусных мер. Исходя из того, что точка О играет роль центральной для данной окружности, \(\angle AOB\) также можно назвать центральным. Градусная мера, в которой исчисляется минимальная дуга, меньше по сравнению с половиной окружности и соответствует центральному углу, опирающемуся на рассматриваемую дугу.
Получим, что минимальная дуга в градусах составляет \(120^{\circ}\). В таком случае максимальная из пары дуга равна \(240^{\circ}\). Сравним полученные характеристики величин:
\(240 \div 120 = 2\)
Ответ: 2.
Имеется пара окружностей, центральные точки которых совпадают и обозначены за О. При этом выполняются следующие условия: OB = 3 OA = 1 \(\angle BOD = 90^\circ\) Требуется вычислить, чему равно значение отношения площади фигуры \(ABCDEFA и \pi\).
Источник: shkolkovo.net
Решение
Сектор с углом \(90^\circ \) в большой окружности обладает площадью, которую можно вычислить таким образом:
\(S_{big} = \frac{\pi\cdot3^2}{360^\circ}\cdot90^\circ = \frac{9\pi}{4}\)
С другой стороны:
\(S_{small} = \frac{\pi\cdot1^2}{360^\circ}\cdot90^\circ = \frac{\pi}{4}\)
В результате:
\(\frac{S_{ABCDEFA}}{\pi} = \frac{S_{big} - S_{small}}{\pi} = 2\)
Ответ: 2.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так