Что нужно знать о формуле Герона — основные сведения

Формулировка теоремы Герона

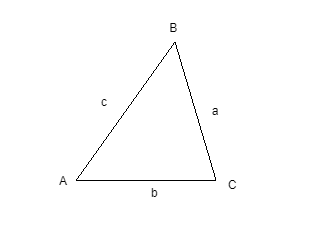
Изобразим рассматриваемый треугольник с заданными параметрами сторон a, b и c:

История формулы Герона

Соотношение, выведенное Героном, упрощает вычисление площади треугольника при условии, что известны значения длин его сторон. Данная формула входит в состав «Метрики» авторства греческого математика и механика Герона Александрийского. В его честь сформулировано название закономерности.

В спектр вопросов, которыми интересовался Герон, входили треугольники со сторонами, измеряемыми целыми числами. Существует определение для подобных геометрических фигур, которое звучит, как «героновые треугольники». Наиболее простой героновый треугольник именуют египетским треугольником, имеющим прямой угол и стороны, соотносящиеся друг с другом таким образом:

3 : 4 : 5

Формула Герона и ее доказательство

Представим, что имеется некий произвольный треугольник, площадь которого равна S, а длины сторон можно найти, как a, b, c. Тогда формула Герона, применительно к этому треугольнику, примет следующий вид:

\(S={\sqrt {p(p-a)(p-b)(p-c)}}\)

В данном случае р является половиной периметра рассматриваемого треугольника:

\(p={\tfrac {1}{2}}\cdot (a+b+c).\)

Попробуем доказать записанное соотношение с точки зрения тригонометрии:

\(S={1 \over 2}ab\cdot \sin {\gamma },\)

где \(\gamma \) обозначает угол треугольника, расположенный напротив стороны с.

Воспользуемся теоремой косинусов:

\(c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma\)

В результате применения теоремы получим:

\(\cos \gamma ={a^{2}+b^{2}-c^{2} \over 2ab}\)

Таким образом:

\(\ \sin ^{2}\gamma =1-\cos ^{2}\gamma =(1-\cos \gamma )(1+\cos \gamma )=\)

\(={{2ab-a^{2}-b^{2}+c^{2}} \over 2ab}\cdot {{2ab+a^{2}+b^{2}-c^{2}} \over 2ab}=\)

\(={{c^{2}-(a-b)^{2}} \over 2ab}\cdot {{(a+b)^{2}-c^{2}} \over 2ab}={1 \over 4a^{2}b^{2}}(c-a+b)(c+a-b)(a+b-c)(a+b+c).\)

Заметим следующее:

\(a+b+c=2p\)

\(a+b-c=2p-2c\)

\(a+c-b=2p-2b\)

\(c-a+b=2p-2a\)

В таком случае:

\(\sin \gamma ={2 \over ab}{\sqrt {p(p-a)(p-b)(p-c)}}\)

На основании расчетов можно прийти к выводу:

\(S={1 \over 2}ab\sin \gamma ={\sqrt {p(p-a)(p-b)(p-c)}}\)

В результате, формула Герона доказана.

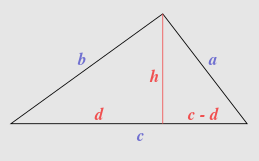
Существует и другой способ подтверждения справедливости формулы Герона. Воспользуемся теоремой Пифагора. Представим, что имеется некий треугольник, стороны которого a, b, c, а высота, обозначенная за h, делит основание c на d и (c − d). Исходя из теоремы Пифагора, запишем равенство гипотенуз:

\(a2 = h2 + (c − d)2 \) и \(b2 = h2 + d2\)

Определим d с помощью сторон треугольника:

\(d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}\)

Подставим это соотношение в уравнение \(h2 = b2 − d2 \) для высоты h и воспользуемся формулой для квадратов:

\({\begin{aligned}h^{2}&=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}={\frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\\&={\frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={\frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\\\end{aligned}}\)

Заметим следующее:

\(b+c-a=2p-2a\)

\(a+b+c=2p\)

\(a+b-c=2p-2c\)

\(a-b+c=2p-2b\)

В результате:

\({\begin{aligned}h^{2}&={\frac {2(p-a)\cdot 2p\cdot 2(p-c)\cdot 2(p-b)}{4c^{2}}}={\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}\end{aligned}}\)

Применим ключевое уравнение для площади треугольника:

\(S={\frac {ch}{2}}\)

Выполним подстановку записанного равенства в уравнение для h, получим:

\({\begin{aligned}S={\sqrt {{\frac {c^{2}}{4}}\cdot {\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={\sqrt {p(p-a)(p-b)(p-c)}}\end{aligned}}\)

Таким образом, формула Герона доказана.

Формула Герона адаптирована для вычисления площади четырехугольника. Полученное соотношение называют формулой Брахмагупты. Согласно установленной закономерности, площадь четырехугольника, вокруг которого описана окружность, определена в виде функции длин его сторон.

Представим, что имеется некий четырехугольник, стороны которого в длину составляют a, b, c, d. Полупериметр рассматриваемой фигуры равен:

\(p={\frac {a+b+c+d}{2}}\)

При таких условиях площадь четырехугольника будет определена следующим образом:

\(S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}.\)

Докажем записанное соотношение. Известно, что площадь четырехугольника, который вписан в окружность, соответствует сумме \(\triangle ABD\) и \(\triangle BDC\):

\(S={\frac {1}{2}}ab\sin A+{\frac {1}{2}}cd\sin C\)

Зная, что четырехугольник \(ABCD\) вписан в окружность, запишем следующее:

\(\angle DAB=180^{\circ }-\angle DCB\)

Таким образом:

\(\sin A=\sin C\)

Из чего следует, что:

\(S={\frac {1}{2}}ab\sin A+{\frac {1}{2}}cd\sin A\)

\(S^{2}={\frac {1}{4}}\sin ^{2}A(ab+cd)^{2}\)

\(4S^{2}=(1-\cos ^{2}A)(ab+cd)^{2}\)

\(4S^{2}=(ab+cd)^{2}-\cos ^{2}A(ab+cd)^{2}.\)

Сформулируем теорему косинусов для стороны \(СВ\) в \(\triangle АСВ\) и \(\triangle BDC\), получим:

\(a^{2}+b^{2}-2ab\cos A=c^{2}+d^{2}-2cd\cos C\)

Заметим, что:

\(\cos C=-\cos A\)

Таким образом, А и С являются противолежащими. Если вынести за скобки \(2\cos A\), то получится:

\(2\cos A(ab+cd)=a^{2}+b^{2}-c^{2}-d^{2}\)

Выполним подстановку полученного выражения в начальную формулу:

\(4S^{2}=(ab+cd)^{2}-{\frac {1}{4}}(a^{2}+b^{2}-c^{2}-d^{2})^{2}\)

\(16S^{2}=4(ab+cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}\)

Воспользуемся следующим соотношением:

\(x^{2}-y^{2}=(x+y)(x-y)\)

В результате:

\((2(ab+cd)+a^{2}+b^{2}-c^{2}-d^{2})(2(ab+cd)-a^{2}-b^{2}+c^{2}+d^{2})\)

\(=((a+b)^{2}-(c-d)^{2})((c+d)^{2}-(a-b)^{2})\)

\(=(a+b+c-d)(a+b+d-c)(a+c+d-b)(b+c+d-a)\)

Зная, что \(p={\frac {a+b+c+d}{2}}\), запишем следующее:

\(16S^{2}=16(p-a)(p-b)(p-c)(p-d)\)

Извлечем квадратный корень и выполним преобразования:

\(S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}.\)

Формула Герона применима к задачам на вычисление площади трапеции. Тогда доказанная ранее закономерность примет следующий вид:

\(S =\frac{a+b}{|a-b|}\sqrt{(p-a)(p-b)(p-a-c)(p-a-d)}\)

\(p=\frac{a+b+c+d}{2}\)

Вариации и обобщения

Существует несколько эквивалентных формул Герона, полученных путем записи полупериметра с помощью полусуммы всех сторон рассматриваемого треугольника:

\(S={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}\)

\(S={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}\)

\(S={\frac {1}{4}}{\sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}\)

\(S={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}\)

Используя определитель, допустимо сформулировать теорему Герона таким образом:

\(- 16S^{2} = {\begin{vmatrix}0&a^{2}&b^{2}&1\\a^{2}&0&c^{2}&1\\b^{2}&c^{2}&0&1\\1&1&1&0\end{vmatrix}} = {\begin{vmatrix}a&b&c&0\\b&a&0&c\\c&0&a&b\\0&c&b&a\end{vmatrix}}\)

Первый определитель последнего соотношения представляет собой частный случай определителя Кэли — Менгера, который используют при расчете гиперобъема симплекса.

Допустимо выразить площадь треугольника по формуле Герона с помощью длин медиан \(m_{a}, m_{b}\) и \(m_{c}\), а также половину их суммы \(\sigma =(m_{a}+m_{b}+m_{c})/2\):

\(S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}\)

Формула Герона будет преобразована, если в расчетах использовать длины высот \(h_{a}, h_{b}\) и \(h_{c}\) и полусумму их обратных величин \(H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2[3]\):

\(S^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}\)

Запишем интерпретацию формулы Герона для вычисления площади треугольника по его углам \(\alpha, \beta\)  и \(\gamma\), полусумме их синусов \(s=(\sin \alpha +\sin \beta +\sin \gamma )/2\) и диаметру описанной окружности \(D={\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}\):

\(S=D^{2}{\sqrt {s(s-\sin \alpha )(s-\sin \beta )(s-\sin \gamma )}}\)

Если четырехугольник вписан в окружность, то значение его площади целесообразно рассчитать с помощью формулы Брахмагупты:

\(S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}\)

Здесь полупериметр четырехугольника вычисляется следующим образом:

\(p={\frac {a+b+c+d}{2}}\)

Формула Брахмагупты, с помощью которой можно решать задачи на поиск площади, выраженная с помощью определителя:

\(S={\frac {1}{4}}{\sqrt {-{\begin{vmatrix}a&b&c&-d\\b&a&-d&c\\c&-d&a&b\\-d&c&b&a\end{vmatrix}}}}\)

Примеры задач на использование формулы Герона