Четная и нечетная функции
Что такое четная функция
Функция f(х) является четной в том случае, когда для каких-либо значений, принимаемых за х и составляющих область, где определяется рассматриваемая функция, справедливо данное соотношение:
\(f(-х)=f(х)\)
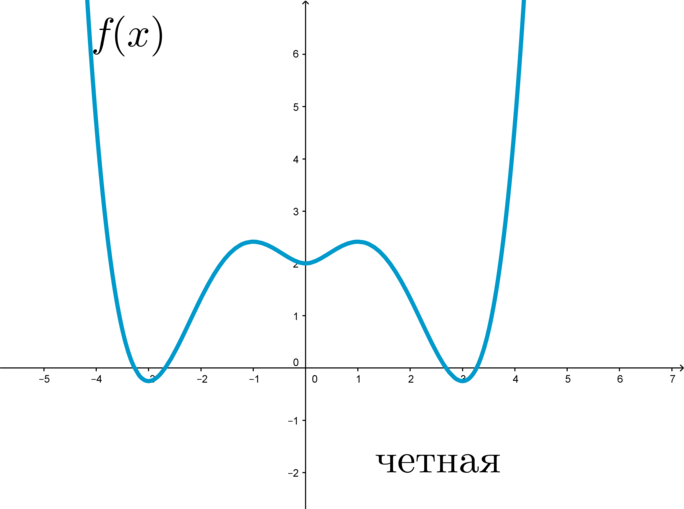
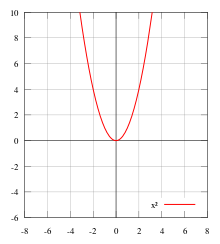
На координатной плоскости четная функция расположена симметрично по отношению к оси ординат. Рассмотрим в качестве примера некую функцию:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(f(х)=х^2+\cos х\)
Данная функция определена, как четная, что просто доказать из этого соотношения:
\(f(-x)=(-x)^2+\cos{(-x)}=x^2+\cos x=f(x)\)
Изобразим график:
Что такое нечетная функция
Функция f(х) определена, как четная в той ситуации, когда какое-либо из всех х, согласно области, где проходит рассматриваемая функция, обращает данное соотношение в верное равенство:
\(f(-х)=-f(х)\).
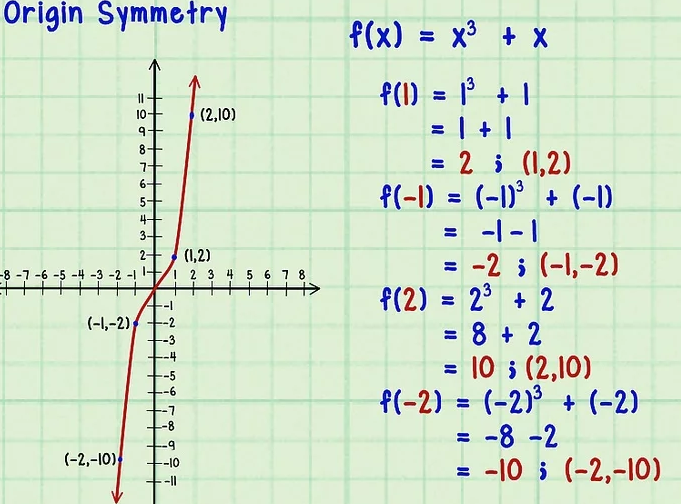
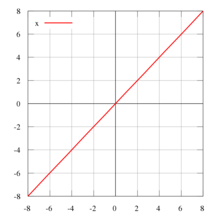
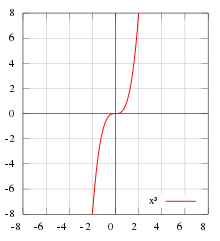
Графически нечетную функцию изображают симметрично по отношению к началу координат. В качестве примера можно привести такой график:
Данный график соответствует функции:
\(f(х)=х^3+х\)
Эта функция нечетная по той причине, что:
\(f(-х)=(-х)^3+(-х)=-х^3-х=-(х^3+х)=-f(х).\)
Как понять, четная или нечетная функция
Разновидности функций определяют правила нахождения переменных, которые входят в состав уравнений и с помощью которых рассматриваемые функции записаны, а также позволяют идентифицировать положение графика. Заметим, что это значит наличие зависимости принадлежности к тому или иному типу от симметрии. Предусмотрена пара методов определения четности или нечетности анализируемых функций. В первом случае задачу допустимо решать, прибегая к алгебраическим вычислениям. Второй способ заключается в изучении графика в рамках координатной плоскости. Кроме всего прочего, такая информация позволяет спрогнозировать, как будут вести себя на схеме определенные совокупности функций, записанные с помощью тех или иных формул.
Разберем анализ четности функции с точки зрения алгебры. Здесь важно понимание термина противоположных значений переменных. Запись такого значения подразумевает использование знака минуса. Когда изначально переменная записана со знаком минуса, ее противоположным значением является та же переменная, но с положительным знаком. Запишем несколько примеров противоположных значений:
х и –х;
q и –q;
-w и w.
Применительно к выражениям, замена знака переменной может выглядеть следующим образом:
\(f(x)=4x^{2}-7\) и \(f(-x)=4(-x)^{2}-7\)
\(g(x)=5x^{5}-2x\) и \(g(-x)=5(-x)^{5}-2(-x)\)
\(h(x)=7x^{2}+5x+3\) и \(h(-x)=7(-x)^{2}+5(-x)+3.\)
В первую очередь необходимо записать новую функцию \(f(-x)\) в упрощенном виде. Далее требуется выполнить ее сравнение с начальной \(f(x)\). При этом могут пригодиться правила возведения в степень. Согласно этим закономерностям, если возвести в степень с четным значением переменную, имеющую отрицательный знак, результатом станет переменная с положительным знаком. Когда при аналогичных действиях манипуляции производят с нечетной степенью, в итоге получается переменная со знаком минуса.
\(f(-x)=4(-x)^{2}-7\)
\(f(-x)=4x^{2}-7\)
\(g(-x)=5(-x)^{5}-2(-x)\)
\(g(-x)=5(-x^{5})+2x\)
\(g(-x)=-5x^{5}+2x\)
\(h(-x)=7(-x)^{2}+5(-x)+3\)
\(h(-x)=7x^{2}-5x+3\)
Затем необходимо приступить к сравнению полученной пары функций:
- Начальная функция четная тогда, когда знаки соответствующих элементов двух функций будут совпадать, то есть \(f(x)=4x^{2}-7\) и \(f(-x)=4x^{2}-7\).
- Начальная функция нечетная, если соответствующие элементы двух функций имеют разные знаки, то есть \(g(x)=5x^{5}-2x\) и \(g(-x)=-5x^{5}+2x.\)
- Функция принимает общий вид, когда не выполняется ни одно из вышеперечисленных условий, то есть \(h(x)=7x^{2}+5x+3\) и \(h(-x)=7x^{2}-5x+3\).
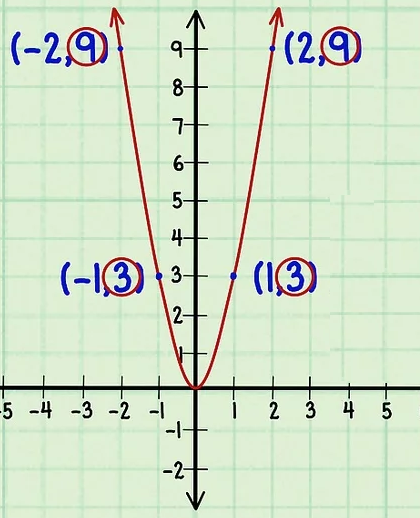
Рассмотрим графический метод решения задач на определение четности функции. На некоторой координатной плоскости следует построить график функции:
\(f(x)=2x^{2}+1\)
Выполним подстановку значений переменной:
\(f(1)=2(1)^{2}+1=2+1=3\), координаты точки (1,3)
\(f(2)=2(2)^{2}+1=2(4)+1=8+1=9\), координаты точки (2,9)
\(f(-1)=2(-1)^{2}+1=2+1=3\), координаты точки (-1,3)
\(f(-2)=2(-2)^{2}+1=2(4)+1=8+1=9\), координаты точки (-2,9).
Расположение графика функции:
- В том случае, когда функция графически представляет собой симметрию по отношению к оси ОУ, можно с уверенностью говорить о четности данной функции.
- Если на некой плоскости с обозначенным началом координат, осями ОХ и ОУ, наблюдается такая ситуация, при которой график симметричен по отношению к точке с координатами (0;0), то следует сформулировать вывод о нечетности рассматриваемой функции.
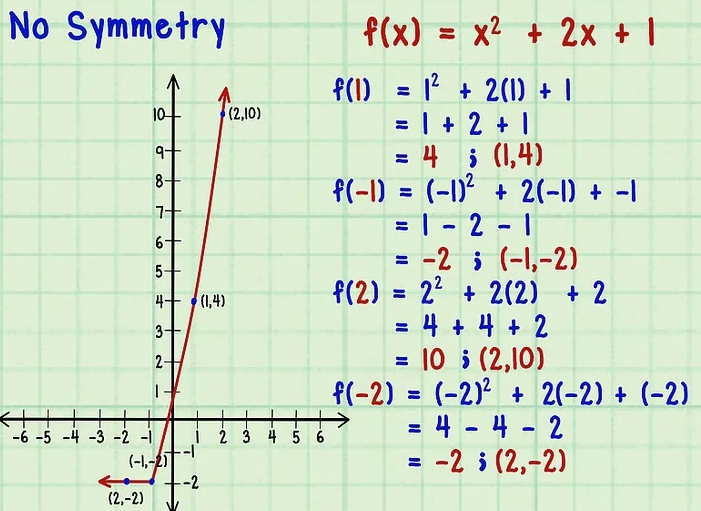
- При отсутствии какого-либо симметричного расположения функция имеет общий вид.
Существует еще две закономерности:
- при четном степенном показателе переменной функция является четной;
- при нечетном степенном показателе переменной функция определена, как нечетная.
Свойства четных и нечетных функций
Перечислим важные свойства, характерные для четных и нечетных функций:
- При действиях \(\div\) или \(\times\) (произведение) пары функций, характеризующиеся аналогичной четностью, получается четная функция.
- При действиях \(\div\) или \(\times\) пары функций, характеризующиеся не одинаковой четностью, получается нечетная функция.
- При действиях + или - функций, определяющиеся, как четные, получается в итоге четная функция.
- При + или - функций, определяющиеся, как нечетные, получается в итоге нечетная функция.
- При условии четности функции f(х) соотношение \(f(х)=c \ (c\in \mathbb{R})\) обладает одним решением при нулевом значении переменной х.
- При условии четности или нечетности функции f(х) соотношение f(x)=0 обладает решением в виде х= b, тогда вторым решением является х= - b.
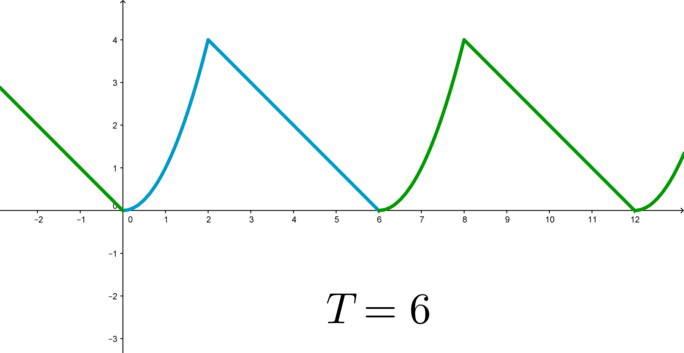
Разберем еще одно важное понятие такое, как периодическая функция f(x) на X при каком-то числе Т, отличном от нуля, когда справедливым является следующее соотношение:
\(f(x)=f(x+T)\)
Здесь \(x+T\in X\).
Минимальное Т при справедливом соотношении, записанном выше, представляет собой ключевой (главный) период функции. Если функция является периодической, то число, записанное, как nT, при \(n\in \mathbb{Z}\) называют периодом.
График периодической функции:
Графики, примеры
Рассмотрим характерные четные и нечетные функции, которые часто можно встретить при решении задач:
Исследование функциональной зависимости на факт четности или нечетности является эффективным методом решения множества задач. В этом случае корректный ответ легко получить, используя алгоритмы, описанные выше. В зависимости от условий используют алгебраический метод или анализируют уравнение на графике.
Записано следующее соотношение:
\(2x^2+a\mathrm{tg}\,(\cos x)+a^2=0\)
Требуется определить, чему равно значение переменной а, если данное равенство обладает единственным корнем.
Решение
К поискам ответа на вопрос задачи следует приступать с исследования условий. Заметим, что следующие функции являются четными:
\(x^2 \) и \(\cos x\)
В связи с этим условием начальное уравнение будет иметь пару решений. Обозначим их таким образом:
\(x_0\) и \(-x_0\)
Далее рассмотрим значения этих неизвестных. Представим, что справедливым является \(x_0\). В таком случае получим следующее соотношение:
\(2x_0^2+a\mathrm{tg}\,(\cos x_0)+a^2=0\), что является справедливым.
Затем проанализируем ситуацию при \(-x_0\). Тогда имеем следующее:
\(2 (-x_0)^2+a\mathrm{tg}\,(\cos(-x_0))+a^2=2x_0^2+a\mathrm{tg}\,(\cos x_0)+a^2=0\).
В результате при условии, что \(x_0\ne 0\), минимальное количество решений записанного равенства равно двум. Из этого можно сделать следующий вывод:
\(x_0=0\)
Путем подстановки значений, ориентируясь на услови задания, получим такое соотношение:
\(2\cdot 0+a\mathrm{tg}\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm{tg}\,1=0 \quad \Rightarrow \quad \left[ \begin{gathered}\begin{aligned} &a=0\\ &a=-\mathrm{tg}\,1 \end{aligned} \end{gathered}\right.\)
Рассмотрим возможность, при которой a=0. Тогда путем подстановки получим выражение в виде:
\(2x^2=0\)
В результате, единственное решение соответствует x=0. Таким образом, путем логичных вычислений придем к заключению о том, что подходящим является корень a=0.
Представим, что:
\(a=-\mathrm{tg}\,1\)
В таком случае соотношение преобразуется следующим образом:
\(2x^2-\mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)+\mathrm{tg}^2\,1=0\)
Здесь целесообразно записать выраждение в такой интерпретации:
\(2x^2+\mathrm{tg}^2\,1=\mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)\)
Заметим, что:
\(-1\leqslant \cos x\leqslant 1\)
Из этого слудет, что:
\(-\mathrm{tg}\,1\leqslant \mathrm{tg}\,(\cos x)\leqslant \mathrm{tg}\,1\)
Справа в полученном соотношении значения расположены в интервале:
\( [-\mathrm{tg}^2\,1; \mathrm{tg}^2\,1]\)
Исходя из того, что \(x^2\geqslant 0\), слева часть соотношения будет превышать, либо соответствовать следующему значению:
\(0+ \mathrm{tg}^2\,1\)
В результате запишем условие, при котором уравнение справедливо:
\(\mathrm{tg}^2\,1\)
Таким образом, путем закономерных преобразований получим следующее математическое соотношение:
\(\begin{cases} 2x^2+\mathrm{tg}^2\,1=\mathrm{tg}^2\,1 \\ \mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)=\mathrm{tg}^2\,1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x=0\\ \mathrm{tg}\,(\cos x)=\mathrm{tg}\,1 \end{cases}\quad\Leftrightarrow\quad x=0\)
В результате вычислений, имеем, что:
\(a=-\mathrm{tg}\,1\)
По итогам расчетов можно записать ответ.
Ответ: \(a\in \{-\mathrm{tg}\,1;0\}.\)
Имеется некая функция, которая описана следующим соотношением:
\(f(x)=3\mathrm{tg}\,\dfrac{ax}5 +2\sin \dfrac{8\pi a-3x}4\)
Нужно вычислить такие значения переменной а, при которых график рассматриваемой функции расположен симметрично по отношению к точке с координатами (0;0).
Решение
Проанализируем исходные данные в примере. Заметим, что выполнение условия задачи возможно лишь в том случае, когда функция определена, как нечетная. Сформулируем этот вывод в математической форме, то есть:
\(f(-x)=-f(x)\)
Исходя из вышесказанного, преобразуем начальное выражения из условия примера и запишем следующее справедливое равенство:
\(\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\[3ex] \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\)
Рассмотрим, чему соответствует область определения последнего соотношения. Запишем следующее верное соотношение:
\(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb{Z}.\)
Полученные значения для а сформулируем в виде ответа и запишем его.
Ответ: \(\dfrac n2, n\in\mathbb{Z}.\)
Дано следующее соотношение:
\(a^2-7a+7\sqrt{2x^2+49}=3|x-7a|-6|x|\)
Необходимо вычислить такое значение а, при котором записанное равенство обладает минимум одним решением.
Решение
Руководствуясь изученным теоретическим материалом и справедливыми закономерностями, выполним преобразования уравнения из условий задачи. В итоге получим следующее верное соотношение:
\(7\sqrt{2x^2+49}=3|x-7a|-6|x|-a^2+7a\)
Получилась пара функций, которые необходимо проанализировать. Запишем данные функции по очереди:
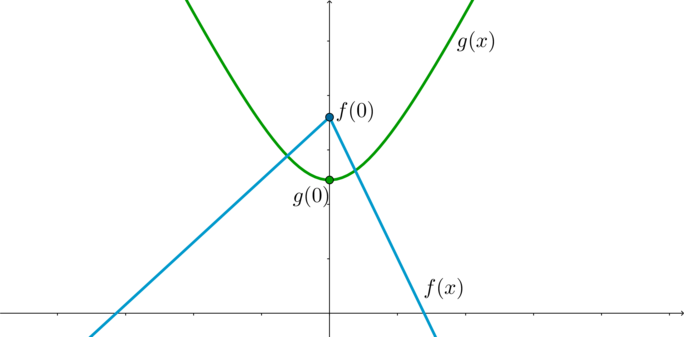
\(g(x)=7\sqrt{2x^2+49}\)
\(f(x)=3|x-7a|-6|x|-a^2+7a\)
Разберем выражение для записи g(x). Заметим, что в первом случае \(g(x)\) определена, как четная. Ее точка минимума соответствует \(х = 0\):
\(g(0)=49.\)
Затем целесообразно рассмотреть следующую функцию. Примечательно, что вторая функция \(f(x)\), если \(x>0\), убывает. Когда \(x<0\), данная функция возрастает. По этой причине точка максимума соответствует \(х = 0\).
\(f(0)=-a^2+7a+21|a|\)
Детально проанализиурем построенный график функции. Здесь важным замечанием является, что начальное соотношение обладает одним корнем в том случае, когда графики пересекаются. Данное высказывание необходимо представить в математической форме, то есть записать, как такое соотношение:
\(f(0)\geqslant g(0) \quad\Rightarrow\quad -a^2+7a+21|a|\geqslant 49 \quad\Leftrightarrow\quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} a>0\\ a^2-28a+49\leqslant 0 \end{cases}\\ &\begin{cases} a<0\\ a^2+14a+49\leqslant 0 \end{cases}\\ &\begin{cases} a=0\\ 0\geqslant 49\end{cases} \end{aligned} \end{gathered}\right.\)
После всех вычислений и преобразований разумно сформулировать окончательный ответ в виде значений, которые принимает а, исходя из условия задачи:
\(a\in \{-7\}\cup [14-7\sqrt3;14+7\sqrt3]\)
Ответ: \(a\in \{-7\}\cup[14-7\sqrt3;14+7\sqrt3]\)
Записано следующее равенство:
\(a^2+13|x|+2^{x^2+2}=20a+2|5x+12a|\)
Требуется вычислить все из возможных значений а, когда данное уравнение обладает, как минимум, одним решением.
Решение
Руководствуясь изученными ранее свойствами функции и справедливыми закономерностями, проанализируем уравнение из условия задачи. Заметим, что его допустимо привести к следующему виду:
\(13|x|-2|5x+12a|=20a-a^2-2^{x^2+2}\)
Далее целесообразно записать пару функций, которые соответствуют следующим соотношениям:
\(g(x)=20a-a^2-2^{x^2+2}\)
\(f(x)=13|x|-2|5x+12a|\)
Исследуем записанные выражения для функций по очереди. Начнем с первой функции \(g(x)\). Данная функция обладает максимальной точкой, которая соответствует \(x=0\). Исходя из этого, разумно сделать следующий вывод:
\(g_{\text{верш}}=g(0)=-a^2+20a-4\)
\(g'(x)=-2^{x^2+2}\cdot \ln 2\cdot 2x\)
Рассмотрим другие варианты, когда х принимает разные значения. К примеру, в том случае, когда \(x<0\), получим следующее: \(g'>0\). Представим такую ситуацию, если \(x>0\). При этом можно прийти к выводу о том, что \(g'<0\). Функция \(f(x)\) при условии, что \(x>0\). Обратный случай, то есть убывание функции можно наблюдать, когда \(x<0\). Можно сделать вывод о равенстве точки минимума нулевому значению.
Обладая достаточными данными и характеристиками поведения функции, выполним соответствующий рисунок
\(f_{\text{верш}}=f(0)=-24|a|\)
Заметим, что на рисунке изображена ситуация, при которой два графика пересекаются между собой в некой координатной плоскости. Такое пересечение графиков пары функций целесообразно записать с помощью следующей системы:
\(f(0)\leqslant g(0) \quad\Rightarrow\quad a^2-20a+4\leqslant 24|a| \quad\Leftrightarrow\quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} a\geqslant 0\\ a^2-44a+4\leqslant 0 \end{cases}\\ &\begin{cases} a<0\\ a^2+4a+4\leqslant 0 \end{cases} \end{aligned} \end{gathered}\right.\)
После выполнения всех необходимых вычислений и преобразований получим, что а с учетом условий, указанных в задании, соответствует следующим значениям:
\(a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]\)
Ответ: \(a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]\).
Требуется рассчитать значения, которые принимает а, при условии наличия у следующего уравнения корней:
\(\cos x+\dfrac32 \cos \dfrac{2x}3+3\cos \dfrac x3=a\)
Решение
Рассмотрим исходные данные. Руководствуясь свойствами функций и стандартным алгоритмом решения подобных примеров, в первую очередь запишем и проанализирует такую функцию:
\(f(x)=\cos x+\frac32 \cos \frac{2x}3+3\cos \frac x3\)
Далее попробуем вычислить основной период, который с учетом вводных характеристик в данном случае составит:
\(у \cos x\) соответствует \(2\pi\)
\(у \cos \frac{2x}3\) соответствует \(\dfrac{2\pi}{\frac23}=3\pi\)
\(у \cos\frac x3\) соответствует \(\dfrac{2\pi}{\frac13}=6\pi\)
В результате главный период соответствует \(6\pi\), что следует из определения этого понятия. Вспомним правила нахождения функций. Запишем условия для наличия у функции корней:
\(\mathrm{min}\,f(x)\leqslant a\leqslant \mathrm{max}\,f(x)\)
Рассмотрим в качестве примера интервал \([0;6\pi]\). Выполним соответствующие преобразования и математические вычисления:
\(f'(x)=\sin x+\sin \dfrac{2x}3+\sin \dfrac x3=0\quad \Rightarrow \quad \left(\sin x+\sin \dfrac{x}3\right)+\sin \dfrac{2x}3=0 \quad \Rightarrow \Rightarrow \quad 2\sin \dfrac{2x}3\cos \dfrac x3+\sin \dfrac{2x}3=0 \quad \Rightarrow \quad \sin \dfrac{2x}3\left(2\cos \dfrac x3+1\right)=0\quad \Rightarrow \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &\dfrac{2x}3=\pi n, n\in\mathbb{Z}\\[3pt] & \dfrac x3=\pm \dfrac{2\pi}3+2\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. \quad \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\dfrac32\pi n, n\in\mathbb{Z}\\[3pt] &x=\pm 2\pi+6\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. \)
Рассмотрим некоторый отрезок \([0;6\pi]\). Заметим, что здесь расположены следующие точки:
\(0;\ \frac{3\pi}2;\ 2\pi;\ 3\pi;\ 4\pi; \ \frac{9\pi}2;\ 6\pi.\)
На следующем этапе потребуется определить, какими знаками обладают полученные интервалы. Используя стандартный алгоритм расстановки плюсов и минусов, допустимо обозначить знаки производной таким образом:
Проанализируем полученные промежутки. Исходя из интервала \([0;6\pi]\), функция обладает самым маленькими значениями в какой-то из точек:
\(\frac{3\pi}2;\ 3\pi;\ \frac{9\pi}2\)
Поступим таким же оборазом, чтобы найти максимумы. Аналогично предыдущим расчетам, максимальными значениями станут следующие:
\(0;\ 2\pi;\ 4\pi; \ 6\pi.\)
В результате поэтапного разбора интервалов и вычислений можно записать такую систему:
\(\begin{aligned} &f(0)=f(6\pi)=\dfrac{11}2\\[4pt] &f\left(\dfrac{3\pi}2\right)=f\left(\dfrac{9\pi}2\right)=-\dfrac32\\[4pt] &f(2\pi)=f(4\pi)=-\dfrac54\\[4pt] &f(3\pi)=-\dfrac52 \end{aligned} \)
Изобразим полученные условия на схеме:
После выполнения всех необходимых расчетов и с учетом логичных выводов целесообразно записать следующие равенства:
\(\mathrm{min}\,f(x)=-\dfrac52, \ \mathrm{max}\,f(x)=\dfrac{11}2.\)
Таким образом, достаточно просто определить значения, которым соответствует а, согласно условиям задачи:
\(a\in\left[-\dfrac52;\dfrac{11}2\right]\)
Ответ: \(a\in \left[-\dfrac52;\dfrac{11}2\right].\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так