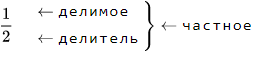Что нужно знать о частном чисел — основные сведения

Что такое частное чисел

Частное пары чисел а и b можно записать в виде простого выражения, чтобы понять суть операции:

\(с = a \div b\)

Здесь а играет роль делимого, а число b является делителем.

Частное пары чисел может быть представлено в виде целого числа. При этом в результате вычислений не ставят какие-либо символы после запятой, также в итоге не могут находиться дробные знаки.

При решении некоторых задач, когда выполняется деление пары чисел, получается в результате некий остаток, который далее невозможно разделить на делитель. В таком случае целесообразно записать его отдельно.

Частное, которое обозначает итог действия деления чисел без остатка, характеризуется таким свойством: при умножении частного на делитель в итоге вычислений получается делимое.

Изменение частного в зависимости от изменения делимого и делителя

Когда ответ получают путем целого деления, делимое можно вычислить с помощью умножения делителя на частное. В результате частное играет роль какого-то из множителей. Изменения в частном возможны при условии замены делимого и делителя.

Если принять один множитель за константу, то уменьшение или увеличение произведения можно наблюдать при изменении второго множителя. Таким образом, при постоянном делителе увеличение делимого в определенное число раз сопровождается увеличением частного в аналогичное число раз.

С такими условиями при уменьшении делимого в какое-то количество раз можно наблюдать уменьшение частного в идентичное количество раз. Данная закономерность демонстрирует изменение делимого и частного в прямом отношении.

Зная, что при неизменном значении одного из множителей произведение может быть увеличено или уменьшено в соответствии с изменениями второго множителя, рассмотрим, как меняется частное, если изменить делимое. Когда делитель является постоянной величиной, увеличение делимого в определенное число раз сопровождается увеличением частного в аналогичное число раз.

Таким же образом, уменьшение делимого в какое-то количество раз приводит к уменьшению частного в идентичное количество раз. Можно сделать вывод о том, что изменения делимого и частного выполняются в прямом отношении.

Проанализируем варианты изменения частного, когда меняется делитель. Вспомним, что произведение неизменно при увеличении одного из множителей и одновременном уменьшении второго множителя в аналогичное количество раз. Справедливо и обратное утверждение.

Исходя из вышесказанного, при постоянном значении делимого увеличение делителя в какое-то число раз сопровождается уменьшением частного в идентичное число раз. С другой стороны, когда уменьшается делитель в определенное количество раз, можно наблюдать увеличение частного в аналогичное количество раз. Заметим, что изменения делителя и частного происходят в обратном отношении.

Нахождение значения частного чисел

При нахождении частного от деления пары чисел, которые не являются дробными, целесообразно поделить их столбиком, когда необходимо вычесть поэтапно результаты умножения цифр, пока не получится нуль. Рассмотрим следующие примеры:

 Порядок вычисления частного от деления дробных чисел, которые являются десятичными:

• умножение делителя и делителя на число 10 в какой-то степени с целью исключения запятой из делителя;
• деление методом в столбик.

При делении обыкновенных дробей следует перевернуть дробь, которая играет роль делителя, а далее умножить полученную дробь на делимое, то есть:

\(\frac{a}{b}\div \frac{c}{d}=\frac{a}{b} \cdot {d}{c}=\frac{a \cdot d} {b \cdot c}\)

В том случае, когда одна из дробей в делителе или делимом обладает целой частью, следует в первую очередь записать ее в виде неправильной дроби.

Задачи, примеры вычисления частного