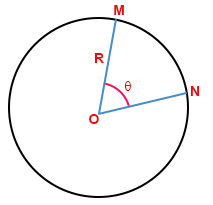
Какой угол называется центральным
Центральный угол — это
Центральный угол — это угол, вычитаемый дугой окружности в центре круга. Радиус-векторы образуют руки центрального угла.
Другими словами, это угол, вершиной которого является центр окружности, а плечами — две радиусные линии, пересекающиеся в двух разных точках окружности. Когда эти две точки соединяются, они образуют дугу. Центральный угол — это угол, вычитаемый этой дугой в центре окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: myalfaschool.ru
Два рукава образуют два радиуса круга, пересекая дугу окружности в разных точках. Центральный угол помогает разделить круг на сектора. Кусок пиццы — хороший пример центрального угла. Круговая диаграмма состоит из нескольких секторов и помогает представить различные количества. Транспортир — это простой пример сектора с центральным углом 180º.
Как найти
Формула центрального угла
Формула центрального угла вычисляется с помощью меры дуги и вписанного угла окружности.
Центральный угол конгруэнтен перехваченной дуге. Таким образом: Центральный угол = Перехваченная дуга.
Центральный угол в два раза больше вписанного угла, образованного той же дугой. Таким образом:
Центральный угол = 2 (вписанный угол)
- Центральный угол = длина дуги / радиус.
- Центральный угол = 2 (площадь сектора окружности) / радиус2.
Формулу можно также обозначить следующим образом:
Центральный угол = s * (360/2πr).
Здесь s — длина дуги, а r — радиус окружности. Это формула для нахождения центрального угла в градусах. Чтобы найти центральный угол в радианах, нужно разделить длину дуги на длину радиуса окружности.
Согласно теореме о мере центрального угла, угол, образованный дугой в центре окружности, в два раза больше угла, образованного ею в любой другой точке окружности. Или: Теорема о центральном угле гласит, что центральный угол окружности вдвое больше угла, вычитаемого дугой в другом сегменте окружности.
Чтобы вычислить центральный угол, нужно узнать длину дуги и радиус. Описанные ниже шаги объясняют, как найти центр угла:
- Найдите конечные точки дуги и центральную точку окружности.
- Соедините конечные точки дуги с центром окружности. Также измерьте длины дуги и радиуса.
- Используйте формулу: центральный угол = длина дуги / радиус, чтобы получить меру центрального угла.
Свойства центрального угла
Когда в центре круга образуется центральный угол, мы можем наблюдать определенные свойства фигуры, такие как:
- Мера центрального угла конгруэнтна измерению дуги, которую он пересекает.
- Все конгруэнтные центральные углы образуют конгруэнтные хорды в окружности, и обратное тоже верно.
- Все конгруэнтные центральные углы образуют конгруэнтные дуги в окружности, и обратное также верно.
- Центральный угол в два раза больше вписанного угла, подписанного той же дугой.
- Если бы мы измерили все центральные углы окружности без общей точки, то в сумме получилось бы 360∘.
Знание центрального угла необходимо для решения задач, связанных с углами в окружности. Центральный угол необходим для вычисления длины дуги и площади сектора. Зная меру центрального угла, мы можем легко вычислить другие меры, связанные с этим углом.
Примеры решения задач
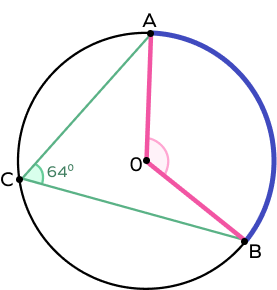
В круге, изображенном ниже, найдите меру ∠AOB.
Источник: splashlearn.com
Решение: Мы знаем, что ∠AOB это центральный угол, а ∠ACB — вписанный угол. Кроме того, центральный угол в два раза больше вписанного, если они вычитаются на одной дуге.
Таким образом, ∠AOB = 2∠ACB
∠AOB = 2(64°)
∠AOB = 128°.
Администрация хочет разбить сад в форме сектора радиусом 42 метра и с центральным углом 120 градусов. Вычислите площадь травы, которая потребуется для покрытия сада.
Решение:
Учитывая, что форма сада — сектор.
Радиус = 42 фута, центральный угол = 120°.
Площадь травы, необходимой для покрытия сада, равна площади сектора.
Площадь сектора = θ/360° × π r2
Площадь = (120°/360°) × π × 422
Площадь = 1/3 × 22/7 × 42 × 42
Площадь = 22 × 2 × 42
Площадь = 1848.
Таким образом, площадь сектора составляет 1848 квадратных метров.
Предположим, что человек A разделил окружность на четыре равные части двумя диаметрами, как измерить центральный или вписанный угол каждой части такой окружности?
Решение: Мы знаем, что полный угол в окружности = 360°.
Так как окружность разделена на 4 равные части, то угол каждой части 360/4.
Центральный угол каждого четырехугольника будет равен 90°.
Ученик измеряет угол в треугольнике с помощью транспортира как 60º. Переведите угол в радианную меру.
Решение: Данный угол 60º имеет шестидесятиричную меру.
Радиан = π/180° × сексагенарий (основание 60)
Радиан = π/180° × 60°
Радиан = π/3.
Следовательно, центральный угол равен π/3 радиана.
Если длина дуги равна 11 см, а радиус окружности равен 7 см, каков будет угол дуги? (Используйте п=227).
Решение: Мы знаем, что s * (360/2πr), где s — длина дуги, а r — радиус окружности.
Центральный угол = (11*360) / 2 * (22/7) * 7 = 90°.
Угол будет равен 90°.
Саша нарисовал круг и разрезал его на четыре равные части, используя два диаметра. Как вы можете помочь ему измерить центральный угол или вписанный угол каждой части окружности?
Решение: Саша разрезал окружность на четыре равные части.
Полный угол в окружности = 360°, угол каждого квадранта = 360°/4 = 90°.
Таким образом, центральный угол квадранта равен 90°.
Если длина дуги окружности равна 8 см, а центральный угол составляет 120°, то каков будет радиус такой дуги? (Используйте п=3,14).
Решение: Мы знаем, что центральный угол равен 120°, а длина дуги равна 8 см.
Используя формулу s * (360/2πr), вычислим:
120° = 8 * (360/2πr)
r = (8*360) / (2п*120)
r = 3,821.
Радиус дуги равен 3,821 см.
Маша отмечает дугу длиной 8 сантиметров и измеряет ее центральный угол как 120 градусов. Каков радиус дуги?
Решение: Радиус дуги = 8 см, а центральный угол = 120°.
Центральный угол = (длина дуги × 360°)/(2 π × радиус)
радиус = (длина дуги × 360°)/(2 π × центральный угол)
радиус = (8 × 360°) / (2 π × 120°)
радиус = 12/π.
Следовательно, радиус равен 12/π см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так