Основные элементарные функции: их свойства и графики
Элементарные функции: понятие, построение
Элементарные функции — вид функций, что возможно получить исключительно посредством ограниченного количества действий с арифметическими единицами.
Бывают следующие основные элементарные функции:
- постоянная функция;
- степенная функция;
- корень n-степени;
- показательная функция;
- тригонометрические функции;
- логарифмические функции;
- обратные тригонометрические функции.
Рассмотрим формулы функций в виде таблицы:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
| Вид функции | Формула |
| Константа | y=C |
| Корень n-степени | \(y=\sqrt[n]{x}\) |
| Степенная функция | \(y=x^{a}\) |
| Показательная функция | \(y=a^{x}\) |
| Логарифмическая функция | \(y=\lg_{a}{x}\) |
| Тригонометрическая функция | \(y=\cos{x}; y=\sin{x}; y=\tan{x}; y=\cot{x}\) |
| Обратные тригонометрические функции | \(y=\arccos{x}; y=\arcsin{x}; y=\arctan{x}\) |
Классификация функций
Постоянная функция
Данный вид функции задают на некотором количестве действительных цифр посредством выражения y=C. В данной формуле C является каким-то действительным значением. В рамках постоянной функции всем показателям свободной переменной x задается одинаковая величина переменной y, которая находится в зависимости. Данная функция именуется константой.
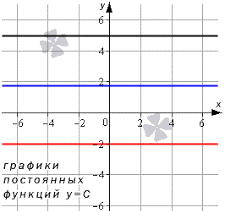
У этой функции есть свой график. Он представляет собой прямую, которая параллельна абсциссионной оси, проходит через точку, которая располагается на (0, C).
Так выглядит график:
Источник: cleverstudents.ru
В качестве образца используем график с разными показателями. Показателю y=-2 соответствует красная полоса; y=5 соответствует черная полоса; \(y=\sqrt{3}\) соответствует синяя полоса.
Свойства константы
К основным свойствам данной функции можно отнести:
- зона распространения — все действительные значения;
- функция четная;
- зона величин — множество, что состоит из одного значения C;
- не возрастает и не убывает;
- не вогнута и не выпуклая;
- не существует асимптот;
- функцию проводят сквозь значение (0, C) плоскости координат.
Корень n-степени
Данная функция обусловливается формулой \(y=\sqrt[n]{x}\). В этой формуле показатель n является натуральной цифрой, которая больше одного. Рассмотрим несколько вариантов случаев функции. Бывают варианты, при которых показатель n является:
- четным значением;
- нечетным значением.
Четное значение n
Разберем, как ведет себя функция при четном значении n.
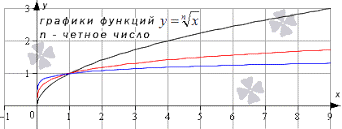
Так выглядит график:
Источник: cleverstudents.ru
На графике можно видеть, что \(y=\sqrt{x}\) — черная полоса; \(y=\sqrt[4]{x}\) — красная полоса; \(y=\sqrt[8]{x}\) — синяя полоса. По тому же принципу строятся графики данной функции с иными величинами.
Что свойственно данной функции при четных значениях n:
- зона распространения — все действительные положительные цифры \(\left[0;+\infty\right)\);
- в случае x=0 у данной функции будут значения в 0;
- имеет универсальный вид;
- зона величин — \(\left[0;+\infty\right)\);
- в случае четных значений растет в зоне распространения;
- выпуклая, имеет направление вверх, не имеет значений перегиба;
- не существует асимптот;
- график проводят через значения (0, 0), а также (1, 1).
Нечетное значение n
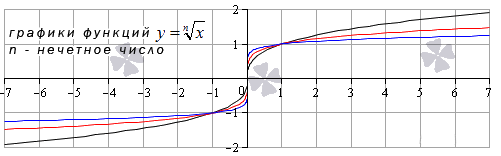
Нечетное значение распространяется на все разнообразие действительных цифр. Так выглядит график:
Источник: cleverstudents.ru
На графике можно видеть, что значение \(y=\sqrt[3]{x}\) — черная кривая; \(y=\sqrt[5]{x}\) — красная; \(y=\sqrt[9]{x}\) — синяя. В других случаях у графика будет примерно такой же внешний вид.
Что свойственно данной функции при нечетных значениях:
- зона распространения — все разнообразие действительных цифр;
- нечетность;
- зона величин — все разнообразие действительных цифр;
- данная функция в случае нечетных значений растет в зоне распространения;
- имеет вогнутость в области \(\left(-\infty;0\right]\) , а также выпуклость в области \(\left[0;+\infty\right)\);
- точкой перегиба является значение (0, 0);
- не существует асимптот;
- в случае нечетных значений график задают через точки (1, 1); (0, 0), (-1, -1).
Степенная функция
Данную функцию можно задать при помощи \(y=x^{a}\). В курсе алгебры есть различные задачи и задания на степенные функции, которые меняются по своей сути от величины степенного показателя.
Самым классическим примером степенной функции является функция, у которой в показателе цельное значение a. Данный вариант графика строится, исходя из того, каков показатель — четный он или нечетный, отрицательный или положительный. Первостепенно исследовать степенные функции формата \(y=x^{a}\) в случае нечетных величин показателя со знаком +. Потому нужно разобрать, как ведут себя функции пр четных величинах со знаком +. А далее уже исследовать характер нечетных и четных величин со знаками + и -.
Особенности степенных функций с показателями в виде дробей или иррациональных выражений (а также форма графика данных функций) находятся в зависимости от величины значения a.
Степенная функция, у которой показатель нечетный, но со знаком плюс
Для начала нужно исследовать характер функции \(y=x^{a}\) в случае нечетности и положительности степенной величины. Получается, что величины могут быть только вроде a=1, a=5 и т.д.
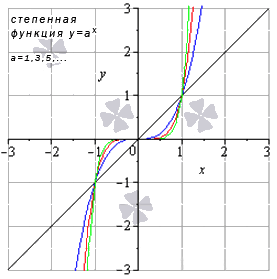
Так выглядит график:
Источник: cleverstudents.ru
На графике можно увидеть разные степенные функции. Так, черная полоса указывает на y=x; синяя — \(y=x^{3}\); красная — \(y=x^{5}\); \(y=x^{7}\)— зеленая. В случае значения показателя a, равного единице, получится линейная функция y=x.
Что свойственно данной функции при нечетных значениях со знаком плюс:
- зона распространения — \(x\in\left(-\infty;+\infty\right)\);
- зона величин — \(y\in\left(-\infty;+\infty\right)\);
- нечетность функции возникает из-за: \(y\left(-x\right)=-y\left(x\right)\);
- возрастание функции происходит в случае \(x\in\left(-\infty;+\infty\right)\);
- выпуклость функции наблюдается в случае \(x\in\left(-\infty;0\right]\), а вогнутость наблюдается в случае \(x\in\left[0;+\infty\right)\) (не в случае линейного вида функции);
- точка перегиба — (0, 0);
- не наблюдается асимптот;
- функцию проводят через точки (1,1), (0,0), (-1,-1).
Степенная функция, у которой четное значение со знаком плюс
К степенным функциям такого типа относятся такие, которые задаются формулой \(y=x^{a}\), но при этом степенной показатель равен 2, 6 или другим четным цифрам.
Так выглядит график:
Источник: cleverstudents.ru
На графике располагаются значения \(y=x^{2}\) (черный цвет); \(y=x^{4}\) (синий цвет); \(y=x^{8}\)(красный цвет). В случае показателя a=2 получается квадратичная по виду функция. У данной функции будет график в виде квадратичной параболы.
Что свойственно данной функции при четных значениях со знаком плюс:
- зона распространения — \(x\in\left(-\infty;+\infty\right)\);
- зона величин — \(y\in\left[0;+\infty\right)\);
- четность функции, из-за того, что \(y\left(-x\right)=y\left(x\right)\);
- рост функции происходит на \(x\in\left[0;+\infty\right)\), убывание происходит на \(x\in\left(-\infty;0\right]\) ;
- вогнутость функции наблюдается в случае\(x\in\left(-\infty;+\infty\right)\) ;
- точки перегиба нет;
- не наблюдается асимптот;
- функцию проводят через точки (1,1), (0,0), (-1,-1).
Степенная функция, у которой значение нечетное и знак минус
В данном случае степенные показатели равняются a=-1; a=-5 и т.д.
Так выглядит график:
Источник: cleverstudents.ru
Черным цветом на графике показано значение \(y=x^{-9}\) ; синим цветом — \(y=x^{-}5\); красным цветом — \(y=x^{-3}\); зеленым цветом — \(y=x^{-1}\). В случае a=-1 будет наблюдаться обратная пропорциональность. В данном случае график — гипербола.
Что свойственно данной функции при нечетных значениях со знаком минус:
- зона распространения функции — \(x\in\left(-\infty;0\right)\cup\left(0;+\infty\right)\);
- в случае x=0 появляется разрыв, потому что \(\lim_{x \rightarrow 0-0}x^{a}=-\infty, \lim_{x \rightarrow 0+0}x^{a}=+\infty\), причем показатель a равен нечетному отрицательному значению — так прямая станет вертикальной асимптотой;
- зона величин — \(y\in\left(-\infty;0\right)\cup\left(0;+\infty\right)\);
- наблюдается нечетность функции, из-за того что \(y(-x)=-y(x)\) ;
- происходит убывание функции в случае \(x\in\left(-\infty;0\right)\cup\left(0;+\infty\right)\);
- выпуклость можно увидеть в случае \(x\in\left(-\infty;0\right)\), а вогнутость в случае \(x\in\left(0;+\infty\right)\) ;
- не наблюдаются точки перегиба;
- горизонтальная асимптота — прямая при y=0, потому что \(k=\lim_{x \rightarrow \infty}\frac{x^{a}}{x}=0, b=\lim_{x \rightarrow \infty}(x^{a}-kx)=0\Rightarrow{y}=kx+b=0\) при значениях a=-1, например;
- функцию проводят через точки (1,1), (-1,-1).
Логарифмическая функция
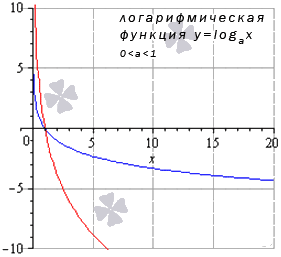
Другая элементарная функция — логарифмическая функция с формулой \(y=\lg_{a}{x}\). В данном выражении \(a>0, a\neq1\). Данную функцию задают исключительно для величин со знаком плюс. То есть, значение аргумента должно быть \(a>0, a\neq1\). У графика данной функции есть самые разные формы, которые зависят от величины основания a.
Для начала рассмотрим вариант, при котором 0<a<1.
Так выглядит график:
Источник: cleverstudents.ru
Посмотрите на график: синий цвет — \(a=\frac{1}{2}\); красный цвет — \(a=\frac{5}{6}\). В случае иных величин, которые не больше 1, у графика будет похожая форма.
Что свойственно данной функции при основании, которое меньше одного:
- зона распространения функции — \(x\in\left(0;+\infty\right)\);
- в случае, когда в правой стороне x стремится прийти в ноль, показатели функции стремятся к положительной бесконечности;
- зона величин — \(y\in\left(-\infty;+\infty\right)\);
- универсальный вид функции;
- наблюдается убывание по всей зоне определения;
- вогнутость наблюдается в случае \(x\in\left(0;+\infty\right)\);
- не наблюдается точек перегиба;
- не наблюдаются асимптоты;
- функцию проводят через точку (1,0).
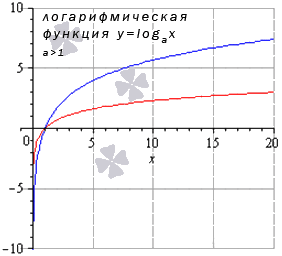
Теперь рассмотрим вариант, при котором основание у такой функции больше одного, то есть a>1.
Так выглядит график:
Источник: cleverstudents.ru
Синяя полоса — \(y=\log_{\frac{3}{2}}{x}\); красная полоса — \(y=\ln{x}\). Если у основания будут иные величины, которые превышают 1, график получит похожую форму.
Что свойственно данной функции при основании, которое больше одного:
- зона распространения — \(x\in\left(0;+\infty\right)\);
- если x будет стремиться в правой части к нулю, то величины функции будут стремиться к бесконечности с отрицательным знаком;
- зона величин — все действительные числа, получается: \(y\in\left(-\infty;+\infty\right)\);
- универсальный вид функции;
- рост функции происходит в случае \(x\in\left(0;+\infty\right)\);
- выпуклость функции наблюдается в случае \(x\in\left(0;+\infty\right)\) ;
- не наблюдаются точки перегиба;
- не наблюдаются асимптоты;
- функцию проводят по точке (1,0).
Тригонометрические функции
Абсолютно все тригонометрические функции являются базовыми элементарными функциями. Всем тригонометрическим функциям свойственно быть периодическими, то есть повторяться по величине функций в разных величинах аргумента. Аргументы обычно должны различаться на значение периода в \(f(x+T)=f(x)\), в которой T будет выступать периодом. Из-за этого в характеристиках тригонометрических функций можно найти особенность в виде самого небольшого периода со знаком плюс. К тому же, всем тригонометрическим функциями нужно задать величину аргумента, в случае которых функция приходит в 0.
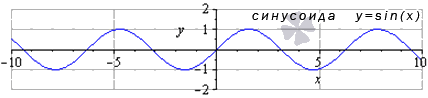
Тригонометрическая функция синуса \(y=\sin{x}\)
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения синусоидальной функции — все разнообразие действительных цифр, получается, что функция \(y=\sin{x}\) задается в случае \(x\in\left(-\infty;+\infty\right)\);
- самый небольшой период со знаком плюс синусоида — \(T=2\pi\);
- обращение функции в ноль произойдет в случае \(x=\pi\times{k}\), при этом \(k\in{z}\), а z — все разнообразие целых значений;
- в синусоиде величина интервала — от -1 до 1, получается, что зона величины — \(y\in\left[-1;1\right]\);
- данная функция нечетная, потому что \(y(-x)=-y(x)\);
- убывание функции наблюдается в случае \(x\in\left[\frac{\pi}{2}+2\pi\times{k};\frac{3\pi}{2}+2\pi\times{k}\right], k\in{z}\);
- возрастание происходит при \(x\in\left[-\frac{\pi}{2}+2\pi\times{k};\frac{3\pi}{2}+2\pi\times{k}\right], k\in{z}\);
- синусоид обладает локальными максимумами в \((\frac{\pi}{2}+2\pi\times{k};1)\) и локальными минимумами в \((-\frac{\pi}{2}+2\pi\times{k};-1)\);
- вогнутость функции наблюдается в случае \(x\in\left[-\pi+2\pi\times{k};2\pi\times{k}\right]\), выпуклость наблюдается при \(x\in\left[2\pi\times{k};2\pi\times{k}\right]\) ;
- точки перегиба функции находятся в \(\pi\times{k;0}\);
- асимптот не наблюдается.
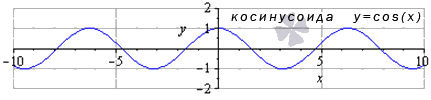
Функция косинуса
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения — \(x\in\left(-\infty;+\infty\right)\);
- самый небольшой период со знаком плюс косинусоида — \(T=2\pi\);
- обращение функции в ноль произойдет в случае \(x=\frac{\pi}{2}+\pi\times{k}\), при этом \(k\in{z}\), а z — все разнообразие целых значений;
- зона величин косинусоида — \(y\in\left[-1;1\right]\);
- функция является четной, потому что \(y(-x)=y(x)\);
- убывание наблюдается в случае \(x\in\left[2\pi\times{k};\pi+2\pi\times{k}\right]\);
- косинусоид обладает локальными максимумами в \((2\pi\times{k};1)\) , а также локальные минимумы в \((\pi+2\pi\times{k};-1)\);
- вогнутость функции наблюдается в случае \(x\in\left[\frac{\pi}{2}+2\pi\times{k};\frac{3\pi}{2}+2\pi\times{k}\right]\), выпуклость наблюдается при \(x\in\left[-\frac{\pi}{2}+2\pi\times{k};\frac{3\pi}{2}+2\pi\times{k}\right];\)
- точки перегиба находятся в \((\frac{\pi}{2}+\pi\times{k};0)\);
- асимптоты не проявляются.
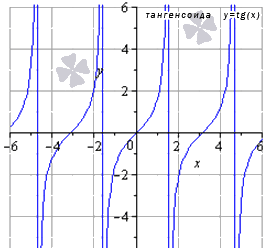
Функция тангенса
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения \(y=\tan{x}\), то есть \(\left(-\frac{\pi}{2}+\pi\times{k};\frac{\pi}{2}+\pi\times{k}\right)\), а z — все разнообразие целых значений;
- характер данной функции в зоне распространения \(\lim_{x \rightarrow \frac{\pi}{2}+\pi\times{k}+0}\tan(x)=-\infty, \lim_{x \rightarrow \frac{\pi}{2}+\pi\times{k}-0}\tan(x)=+\infty\);
- из-за этого прямые \(x=\frac{\pi}{2}+\pi\times{k}\) будут вертикальными асимптотами;
- самым малым периодом со знаком плюс будет период \(T=\pi\);
- функция становится нулем в случае \(x=\pi\times{k}\);
- зона величин — \(y\in\left(-\infty;+\infty\right)\);
- проявляется нечетность функции, потому что \(y(-x)=-y(x)\);
- рост функции наблюдается в случае \(x\in\left(-\frac{\pi}{2}+\pi\times{k};\frac{\pi}{2}+\pi\times{k}\right)\);
- вогнутость наблюдается в случае \(x\in\left[\pi\times{k};\frac{\pi}{2}+\pi\times{k}\right)\), а выпуклость наблюдается при \(x\in\left(-\frac{\pi}{2}+\pi\times{k};\pi\times{k}\right]\);
- точки перегиба находятся в \((\pi\times{k};0)\);
- асимптот не наблюдается.
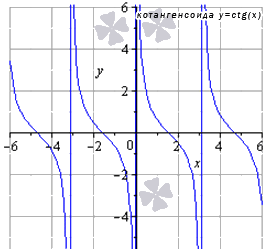
Функция котангенса
Так выглядит график:
Источник: cleverstudents.ru
Обратные тригонометрические функции
Все обратные тригонометрические функции считаются частью элементарных функций. Нередко подобные функции из-за своей сути называют аркфункциями.
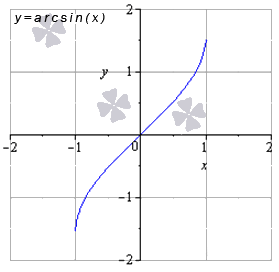
Функция арксинуса
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения арксинуса определяется \(x\in\left[-1;1\right]\);
- зона величин арксинуса — \(y\in\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\);
- функция нечетна, потому что \(y(-x)=-y(x)\);
- рост функции наблюдается в случае, когда \(x\in\left[-1;1\right]\);
- вогнутость функции наблюдается в случае \(x\in\left[0;1\right]\), выпуклость наблюдается в случае \(x\in\left[-1;0\right]\);
- точкой перегиба считается (0,0), то есть полный функциональный ноль;
- асимптоты не наблюдаются.
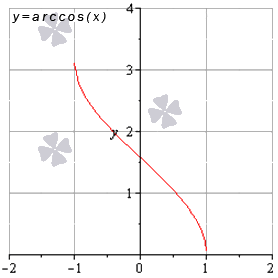
Функция арккосинуса
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения арккосинуса определяется \(x\in\left[-1;1\right]\);
- зона величин \(y=\arccos{x}\) — \(y\in\left[0;\pi\right]\);
- универсальный вид функции;
- наблюдается убывание функции на всей зоне распространения арккосинуса, получается: \(x\in\left[-1;1\right]\);
- вогнутость функции наблюдается в случае \(x\in\left[-1;0\right]\), а выпуклость функции наблюдается в случае \(x\in\left[0;1\right]\);
- точкой перегиба является \(\left(0;\frac{\pi}{2}\right)\);
- асимптот не наблюдается.
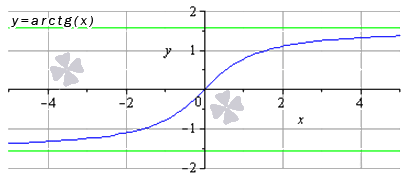
Функция арктангенса
Так выглядит график:
Источник: cleverstudents.ru
Что свойственно данной функции:
- зона распространения данной функции \(\arctan{x}\) — \(x\in\left(-\infty;+\infty\right)\);
- зона величин функции \(\arctan{x}\) — \(y\in\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\);
- проявляется нечеткость арктангенса, потому что \(y(-x)=-y(x)\);
- рост функции наблюдается во всей зоне распространения — \(x\in\left(-\infty;+\infty\right)\);
- вогнутость наблюдается в случае \[x\in\left(-\infty;0\right]\], а выпуклость в случае \(x\in\left[0;-\infty\right)\);
- точкой перегиба считается (0,0), то есть полный функциональный ноль;
- горизонтальная асимптота — прямая \(y=-\frac{\pi}{2}\) при этом \(x\rightarrow{-\infty}\) и \(y=\frac{\pi}{2}\)при \(x\rightarrow{+\infty}\)(в рамках чертежа они изображаются при помощи зеленого цвета).
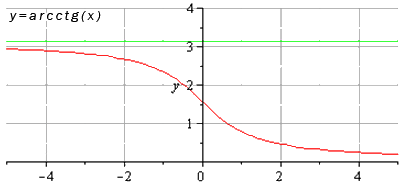
Функция арккотангенса
Так выглядит график:
Источник: cleverstudents.ru
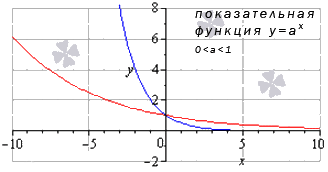
Показательная функция
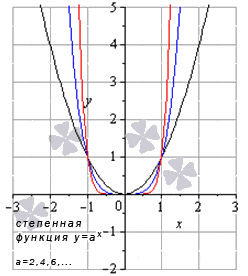
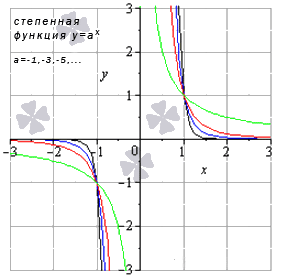
Создается по формуле \(y=a^{x}\).
Так выглядит график в случае значений 0<a<1:
Источник: cleverstudents.ru
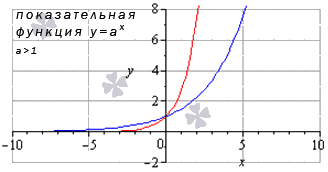
Так выглядит график в случае значения a>1:
Источник: cleverstudents.ru
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так