Оценка генеральной и выборочной дисперсии
Генеральная и выборочная дисперсия
Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:
- размах вариации;
- среднее абсолютное отклонение;
- дисперсия.
Разберем понятие дисперсии, ее виды и свойства.
Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.
Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.
В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.
Дисперсию также делят на два вида в зависимости от используемых данных:
- генеральная дисперсия;
- выборочная дисперсия.
Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.
Выборочная дисперсия, определение, формулы для вычисления
Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как \({\overline y}_в\).
Выборочная дисперсия \(D_в\) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки \(y_1,\;y_2,\;...y_n\) от ее среднего значения \({\overline y}_в\).
Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.
Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:
\(D_в=\frac{{\displaystyle\sum_{i=1}^n}(y_i-{\overline y}_в)}n\)
В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.
\(D_в=\frac{{\displaystyle\sum_{i=1}^k}(y'_i-{\overline y}_в)\cdot n_i}n\)
где \(y'_i \)— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;
\(n_i \)— частота.
Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.
Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:
\(D_в=\frac{{\displaystyle\sum_{i=1}^n}{(y_i-{\overline y}_в)}^2}{n-1}\)
Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.
Генеральная дисперсия, определение, что является оценкой, формулы для вычисления
Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности \(X — {\overline x}_г.\)
Генеральная дисперсия \(D_г\) есть среднее арифметическое отклонение квадратов разности признаков \(x_1,\;x_2,\;...x_n\) генеральной совокупности X от их среднего значения \({\overline x}_г\).
Иногда генеральную дисперсию называют теоретической.
Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:
\(D_г=\frac{{\displaystyle\sum_{i=1}^N}{(x_i-{\overline x}_г)}^2}N\)
и для сформированного вариационного ряда:
\(D_г=\frac{{\displaystyle\sum_{i=1}^K}{(x'_i-{\overline x}_г)}^2\cdot n_i}N\)
Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.
Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.
Оценки параметров распределения
Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.
Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.
Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.
\(\delta=\sqrt D\)
Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).
Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:
\(D=M\left[X-M(X)\right]^2\)
для непрерывной:
\(D=\int_{-\infty}^\infty(x-M{(x))}^2\cdot f(x)dx\)
где f(x) — функция распределения случайной величины.
Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.
Примеры решения задач
Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.
Решение.
Сначала вычислим выборочное среднее значение:
\({\overline x}_в=\frac{210+200+195+205+190+200}6=200\;B.\)
Теперь найдем выборочную дисперсию:
\(D_в=\frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=\frac{250}6\approx42.\)
Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель \(\frac n{n-1} (n=6):\)
\(D_и=\frac n{n-1}\cdot D_в=\frac65\cdot\frac{250}6=50.\)
Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.
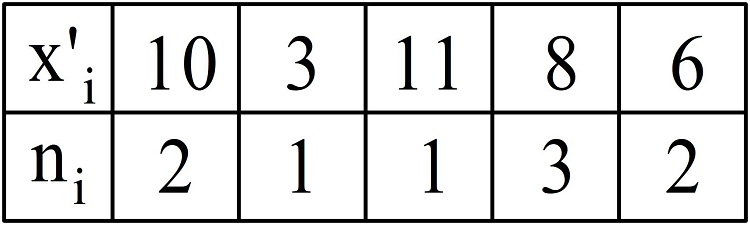
Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.
Решение.
Вычислим выборочную несмещенную дисперсию:
\(D_в=\frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9\cdot\frac98=\frac{398}8\approx50.\)
Теперь найдем среднеквадратическое отклонение:
\(\delta=\sqrt{D_в}=\sqrt{\frac{398}8}=\frac{\sqrt{199}}2\approx7.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так