Сила трения: формула, чему равна, на что направлена
Что такое сила трения
Сила трения, как физическое явление, возникает при соприкосновении и взаимном передвижении двух поверхностей. Данная сила представляет собой объект изучения физики, а именно, механики. В процессе опытных наблюдений и изучения силы трения были сформулированы ключевые закономерности, описывающие перемещение и взаимное воздействие физических тел друг на друга. При этом объясняются причины, в зависимости от которых предметы занимают то или иное положение. Когда формируется некая сила трения, образуется барьер для последующего движения взаимодействующих тел.
Возникновение силы трения можно объяснить взаимным воздействием атомов и молекул. Они входят в состав абсолютно всех окружающих предметов. Исходя из этого, разумно сделать вывод о природе образования силы трения, то есть электромагнитных волнах. Вектор силы трения ориентирован в двух направлениях. Данная сила оказывает действие на оба тела, участвующие во взаимодействии. В этом случае можно наблюдать стабильность значения модуля силы трения. Когда один из предметов рассматриваемой системы испытывает на себе действие силы, она влияет и на второй предмет. Если объект неподвижен, то он подвержен силе трения покоя. Такое состояние отличается стабильностью до того момента, пока сила покоя и сила внешнего смещающего его воздействия уравновешены.
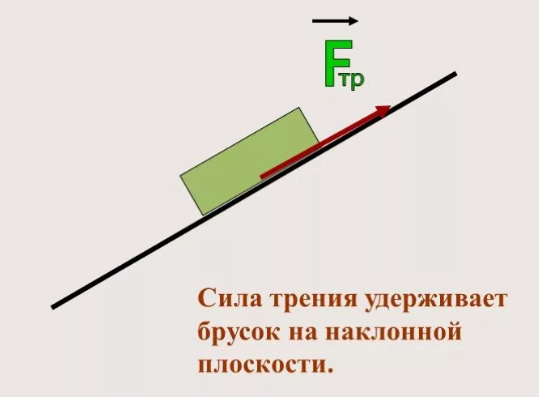
По мере возрастания силы, действующей на тело, кроме силы трения покоя, можно заметить, что оно начинает двигаться и занимает новое положение. Таким образом, проявляется сила трения скольжения, вектор которой направлен противоположно движению объекта. За счет действия силы трения не представляется возможным двигаться в течение неограниченного времени. Перемещение завершается после какого-то временного промежутка. При увеличении внешней силы по сравнению с силой трения покоя можно наблюдать возобновление движения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Трение представляет собой процесс в механике взаимного воздействия тел, которые соприкасаются и перемещаются относительно друг друга в плоскости касания. Также трением называют относительное перемещение между собой параллельных слоев веществ в жидком, газообразном, твердом агрегатных состояниях.
Сила трения является такой силой, причина возникновения которой заключается в соприкосновении пары предметов и которая создает барьер для их относительного перемещения.
От чего зависит сила трения
Силу трения можно наблюдать в окружающем мире повсюду. Благодаря ее действию, тела не двигаются бесконечно, занимают определенное положение. За счет силы трения предметы лишены возможности скользить и перемещаться длительное время. Величина силы трения определяется типом соприкасающихся поверхностей, их физико-химическими свойствами и характеристиками.
Параметром, который не влияет на силу трения, является площадь соприкосновения предметов. С другой стороны, на интенсивность воздействия оказывает влияние то, как расположены тела. К примеру, если машина едет по ровной дороге, на нее действует одна сила. В том случае, когда транспортное средство перемещается по горному рельефу под каким-то углом к горизонту, оно испытывает на себе силу другой величины. Также значение силы поменяется при движении автомобиля по мокрому асфальту.
Трение возникает по причине шероховатости, которой обладают соприкасающиеся поверхности, а также за счет взаимного воздействия молекул, составляющих эти поверхности. Величина возникающей силы трения определяется составом материалов и тем, насколько сильно они соприкасаются друг с другом. Самые простые модели демонстрации силы трения, с помощью которых описан закон Кулона, предполагают прямую пропорциональную зависимость между силой трения и силой нормальной реакции, возникающими между соприкасающимися поверхностями.
Известно, что физико-химические процессы, протекающие в физических телах, отличаются сложностью. По этой причине сформулировать принципы, характерные для процессов трения, с помощью простейших моделей традиционной механики не представляется возможным.
В чем измеряется
Сила трения представляет собой величину, описывающую процесс трения, а именно, его значение и направление. Из школьного курса физики известно, что силу измеряют в Ньютонах (Н). Аналогичные единицы измерения используют при расчете силы трения.
Как найти силу трения: формула
Коэффициент трения (обозначают, как \mu) играет роль ключевой характеристики трения, зависит от состава соприкасающихся поверхностей.
При рассмотрении примитивных примеров возникновения силы трения и нормальной нагрузки данные величины можно выразить с помощью следующего соотношения:
\(|F|\leqslant \mu {N_{{normal}}}\)
Здесь F обозначает силу трения, \(N_{normal}\) является силой нормальной реакции.
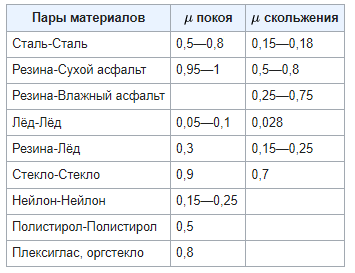
Перечислим некоторые коэффициенты трения, характерные для разных материалов:
Виды силы трения
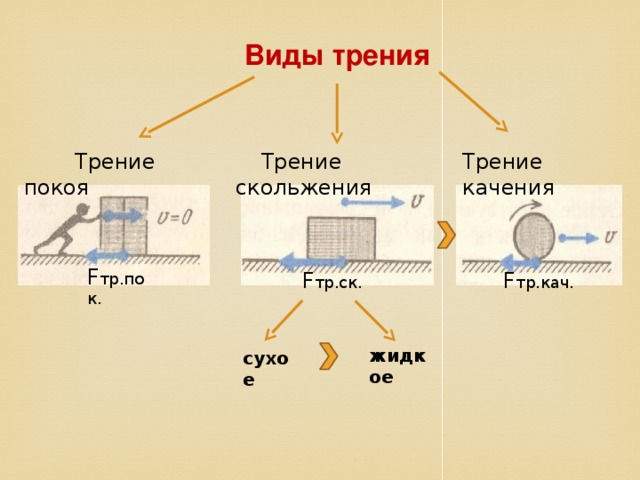
Как уже было сказано ранее, силы трения могут отличаться в зависимости от природы и положения взаимодействующих тел. Рассмотрим основные виды данного воздействия:
- Сила трения покоя направлена против внешнего воздействия, перемещающего предмет. Если внешние силы отсутствуют, сила трения покоя имеет нулевое значение.
- Сила трения скольжения прямо зависит от коэффициента трения и силы давления поверхности, влияющей на тело. Вектор этого трения является перпендикуляром, опущенным к поверхности. В распространенных ситуация скольжение меньше по сравнению с самой большой силой трения покоя.
- Сила трения качения формируется в том случае, когда какой-то предмет катится по поверхности второго. В качестве примеров можно привести движение колеса велосипеда относительно дороги и функционирование подшипникового механизма. Действие этой силы меньше по сравнению со скольжением при аналогичных условиях.
- Сила трения верчения образуется при вращении некого тела относительно поверхности другого тела.
Трение, как природное явление, классифицируют на несколько видов. Перечислим основные из них:
- Сухое трение, редко встречающееся в естественной среде, предполагающее взаимодействие твердых поверхностей.
- Вязкое (жидкостное) трение можно наблюдать, когда твердое тело соприкасается с материалом в жидком или газообразном агрегатных состояниях.
- Смешанное трение характерно для взаимодействия предметов, поверхности которых смазаны.
Кроме того, трение бывает таких видов, как:
- внутреннее;
- внешнее.
Задачи
Доска имеет массу (М) 15 кг и расположена на гладкой поверхности. На нее поместили брусок массой (m) 3 кг. Требуется вычислить, чему равна максимальная горизонтально ориентированная сила, воздействующая на доску, при нахождении бруска в состоянии покоя. Коэффициент трения между доской и бруском в данном случае следует считать за \(\mu = 0,4.\)
Решение
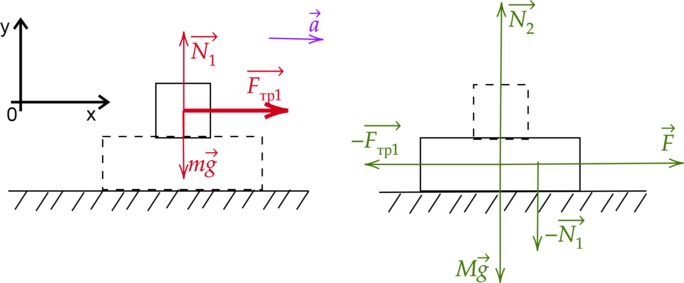
Воспользуемся понятием и особенностями действия сил трения, применительно к данной задаче. Для удобства вычислений необходимо представить два изображения. Сначала продемонстрируем наглядно действие сил, направленных на брусок. С правой стороны изобразим систему сил для доски.
Заметим, что брусок находится в состоянии покоя на доске. Таким образом, можно сделать вывод о равенстве их ускорений, то есть:
\(a_1=a_2=a\)
Воспользуемся вторым законом Ньютона, применительно к бруску. Тогда получим следующее соотношение:
\(\vec{N_1}+\vec{F_{\text{тр}}}+m\vec{g} = m\vec{a}\)
Воспроизведем проекции на координатные оси:
\(Oy: N_1 - mg = 0\)
\(Ox: F_{\text{тр}} = ma\)
В критический момент времени при максимальном значении ускорения. При этом скольжение бруска отсутствует, а сила трения покоя находится в равновесии с силой трения скольжения. Исходя из данных условий, можно записать следующее:
\(F_{\text{тр}} = \mu N = \mu mg\)
Путем подстановки полученного выражения в уравнение проекции второго закона Ньютона на ось Ох, получим такое соотношение:
\(\mu mg = ma \Rightarrow a= \mu g\)
Далее необходимо применить второй закон Ньютона для системы, в которой участвуют доска и брусок. Выглядеть это будет следующим образом:
\(\vec{N_1}+\vec{F_{\text{тр1}}}+m\vec{g} - \vec{N_1} - \vec{F_{\text{тр1}}}+M\vec{g} + \vec{F} + \vec{N_2}= (m+M)\vec{a} m\vec{g} + M\vec{g} + \vec{F} +\vec{N_2} = (m+M)\vec{a}\)
Проекция записанного выражения на ось абсцисс даст такое равенство:
\(F =(m+M)a = (m+M)\mu g F = (3+15)\text{ кг}\cdot 0,4 \cdot 10\text{ м/с$^2$} = 72\text{ H }\)
Ответ: 72.
Некое тело движется, испытывая влияние горизонтально направленной силы. При этом на тело оказывает воздействие сила трения, обозначенная, как \(F_{\text{тр1}}\). Необходимо вычислить, во сколько раз поменяется значение данной силы при уменьшении массы наблюдаемого объекта в 2 раза.
Решение
Упростить понимание этой задачи можно путем изображения всех сил, приложенных к телу:
Воспользуемся вторым законом Ньютона, чтобы записать следующее справедливое равенство:
\(\vec{F} + \vec{N} + m\vec{g} +\vec{F}_{\text{тр1}} = m\vec{a}\)
В данном случае m обозначает массу тела, а является ускорением, которое приобретает объект.
Если построить проекцию данного выражения на вертикальной оси, то получим такое соотношение:
\(N - mg = 0 \Rightarrow N=mg\)
Исходя из понятия силы трения скольжения, справедливо записать следующее уравнение:
\(F_{\text{тр}} = \mu N = \mu mg\)
Здесь \mu является коэффициентом трения.
Заметим наличие прямой зависимости между силой трения скольжения и массой объекта. Из этого целесообразно сделать вывод об уменьшении силы трения скольжения в 2 раза при условии, что массу тела уменьшили в 2 раза.
Ответ: 2
Некий предмет имеет массу 10 кг и испытывает на себе горизонтально ориентированную силу F=30 Н. Данное тело расположено на горизонтальной шероховатой поверхности. Коэффициент трения при этом равен \(\mu=0,5\). Нужно вычислить величину силы трения.
Решение
Обратимся к понятию силы трения скольжения. Данная сила определяется с помощью следующей формулы:
\(F_{\text{ск}} = \mu N\)
В данном случае N обозначает силу реакции опоры.
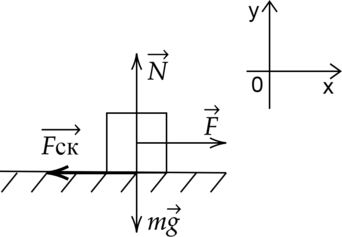
Изобразим схематично силы, которые приложены к предмету:
Воспользуемся вторым законом Ньютона и запишем следующее справедливое равенство, применительно к условиям задачи:
\(\vec{F_{\text{ск}}} +\vec{F}+m\vec{g} + \vec{N} = m\vec{a} \)
Если спроецировать рассматриваемые силы на ось ординат, получим следующее:
\(N-mg=0\Rightarrow N=mg Отсюда: F_{\text{ск}} = \mu mg = 0,5\cdot 10\text{ кг} \cdot 10\text{ м/с$^2$} = 50\text{ H }\)
Из полученного результата можно сделать такой вывод:
\(F_\text{ск} > F\)
Из этого следует, что при приложении к телу силы, направленной в левую сторону, оно начнет двигаться в правую сторону. С точки зрения физики такая ситуация невозможна. Таким образом, вычисленной силы не хватает для смещения предмета. В результате, можно наблюдать равенство силы трения и силы трения покоя, равной силе, с которой воздействуют на тело для его передвижения:
\(F_{\text{тр}}=F_{\text{покоя}} = F = 30\text{ Н }\)
Ответ: 30
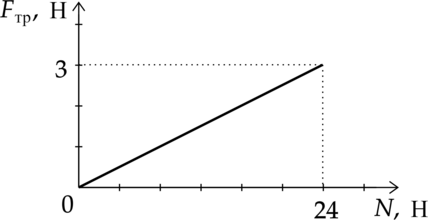
Графически изображена зависимость модуля силы трения скольжения от модуля силы нормального давления. Необходимо вычислить значение коэффициента трения.
Решение
Воспользуемся уравнением силы трения, из которого выразим искомый коэффициент трения. Подставим известные величины по условию задания и выполним вычисления:
\(F_\text{ тр}=\mu N \Rightarrow \mu =\dfrac{F_\text{ тр}}{N}=\dfrac{3\text{ Н}}{24\text{ Н}}=0,125\)
Ответ: 0,125
Предмет перемещается по горизонтальной поверхности и действует на нее с силой 40 Н. Значение силы трения соответствует 10 Н. Необходимо вычислить, чему равен коэффициент трения скольжения.
Решение
Запишем уже знакомую формулу для определения силы трения:
\(F_\text{ тр}=\mu N\)
В данном случае N определяет нормальную составляющую силы воздействия предмета на поверхность.
Выразим коэффициент трения из записанной формулы. Путем подстановки численных значений из условия задания получим искомую величину:
\(\mu =\dfrac{F_\text{ тр}}{N}=\dfrac{10\text{ Н}}{40\text{ Н}}=0,25\)
Ответ: 0,25
Небольшая шайба скользит по наклонной плоскости с углом \(\alpha = 45{^\circ}\) и высотой h. Время движения t=2 с. С наклона \(30^{\circ}\) шайба скользит равномерно. Необходимо вычислить высоту горки и округлить ответ до десятых.
Решение
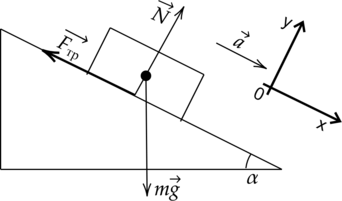
Проанализировать все силы, которые оказывают влияние на шайбу, становится проще, если изобразить их на схеме:
Запишем соотношение для второго закона Ньютона:
\(\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\)
Далее представим проекцию полученного выражения на ось абсцисс и ординат:
\(Ox: mg\sin{\alpha} - F_{\text{тр}}=ma\)
\(Oy: N-mg\cos{\alpha} = 0\Rightarrow N=mg\cos{\alpha}\)
Исходя из понятия силы трения скольжения, запишем следующее уравнение:
\(F_{\text{тр}} = \mu N = \mu mg\cos{\alpha}\)
В результате получим, что:
\(mg\sin{\alpha} - \mu mg\cos{\alpha}=ma g(\sin{\alpha} - \mu \cos{\alpha})=a\)
Проанализируем условия, при которых шайба скользит, чтобы определить значение коэффициента трения. Заметим, что в начале движения ускорение обладает нулевым значением. Таким образом, проекция второго закона Ньютона на ось абсцисс примет следующий вид:
\(Ox: mg\sin{\alpha_{\text{кр}}} - F_{\text{тр}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}} где \alpha_{\text{кр}} = 30^{\circ} F_{\text{тр}} = mg\sin{\alpha_{\text{кр}}} =\mu N = \mu mg\cos{\alpha}\)
В результате:
\(\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\)
Путем подстановки полученного значения в выражение для расчета ускорения получим следующее:
\(a = g(\sin{\alpha} - tg{\alpha_{\text{кр}}}\cdot\cos{\alpha} )\)
Сформулируем кинематическое уравнение:
\(S = \frac{h}{\sin{\alpha}} = \frac{at^2}{2}\)
Здесь S обозначает путь, который преодолела шайба в процессе движения.
Таким образом, вычислим, чему равна высота:
\(h = \frac{at^2}{2}\cdot\sin{\alpha} = \frac{g(\sin{\alpha} - tg{\alpha_{\text{кр}}}\cdot\cos{\alpha})\cdot t^2}{2}\cdot\sin{\alpha} h = \frac{10\text{ м/с$^2$}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{3}}{3}\cdot\dfrac{\sqrt{2}}{2}\right)\cdot4\text{ c$^2$}}{2} \cdot \frac{\sqrt{2}}{2} h=10\cdot\left(1 - \frac{\sqrt{3}}{3}\right)\text{ м} \approx 4,2\text{ м }\)
Ответ: 4,2
Предмет имеет массу 10 кг и расположен на наклонной поверхности с углом наклона \(\alpha= 30^{\circ}\). Коэффициент трения составляет \(\mu=0,4\). Нужно рассчитать силу трения \( F_{\text{тр}}.\)
Решение
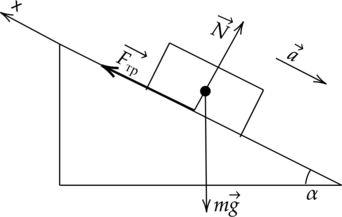
В первую очередь необходимо определить, в каком состоянии находится предмет. Целесообразно при этом проанализировать момент времени равенства угла наклона критическому, то есть:
\(\alpha=\alpha_{\text{кр}}\)
Согласно второму закону Ньютона, получим:
\(\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\)
Запишем проекции уравнения на оси абсцисс и ординат:
\(Ox: F_{\text{тр}}- mg\sin{\alpha_{\text{кр}}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}}\)
\(Oy: N-mg\cos{\alpha_{\text{кр}}} = 0\Rightarrow N=mg\cos{\alpha_{\text{кр}}}\)
Исходя из определения силы трения скольжения, составим следующее соотношение:
\(F_{\text{тр}} = \mu N = \mu mg\cos{\alpha_{\text{кр}}} mg\sin{\alpha_{\text{кр}}} = \mu mg\cos{\alpha_{\text{кр}}}\)
В результате:
\(\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\)
Так как \(\alpha_{\text{кр}}\) является углом, при котором предмет смещается, \(tg{\alpha}\) обозначает функцию, которая возрастает на интервале \((0;\dfrac{\pi}{2})\), можно записать следующий вывод для \(\alpha < \alpha_{\text{кр}}\):
при \(\mu < tg{\alpha}\) предмет начинает скользить;
при \(\mu > tg{\alpha} \) тело находится в покое.
Выполним сравнение \(\mu\) с тангенсом наклона. Отношение примет следующий вид:
\(0,4 < tg{30^{\circ}} \approx 0,6 \Rightarrow \text{тело скользит}\)
В результате, искомая сила сопротивления является силой трения скольжения, вычисляемая таким образом:
\(F_{\text{тр}} = \mu N =\mu mg\cos{\alpha} F_{\text{тр}} = 0,4\cdot 10\text{ кг}\cdot 10\text{ м/с$^2$}\cdot\frac{\sqrt{3}}{2} F_{\text{тр}} \approx 34,6\text{ H }\)
Ответ: 34,6.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так