Как определить силу натяжения нити между двумя телами
Сила натяжения нити — основные понятия, обозначение, единица измерения
Сила натяжения — сила, которую прикладывают к концам объекта, она создает внутри объекта упругую деформацию.
Длина тела, к которому прилагают силу, обычно во много раз больше, чем толщина этого тела. Такими телами могут быть обыденные вещи — канат, веревка, трос, проволока, леска и т. д.
Приведем примеры силы натяжения нити в быту:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- применение отвеса для строительства;
- установка растяжек для того, чтобы зафиксировать радиоантенны;
- характер арматуры внутри напряженного бетона;
- устройство такелажа корабля.
Фото такелажа:
Сила натяжения нити является суммой сил, которые действуют на нить, а также противоположна по своему направлению.
F=-F
Здесь F — сила натяжения. Также встречаются обозначения силы натяжения нити с помощью букв «T» и «N». За единицу измерения у силы натяжения нити принимают Ньютон (сокращенно — H).
Как определить для разных условий, формулы для расчета
Существует множество разных вариантов определения силы напряжения нити. Рассмотрим некоторые из них.
Определение силы натяжения на одной нити
Определение силы натяжения на одной нити происходит в несколько этапов.
Первый этап — нужно определить силы на обоих концах нити. Сила натяжения этой нити или веревки считается результатом сил, которые натягивают веревку с каждого из концов.
Напомним, что сила будет равна произведению массы m на ускорение a.
Предположим, что веревка туго натянута. Каждое изменение массы или ускорения объекта, который подвешен на веревке, приведет к тому, что силы на самой веревке изменятся. Не стоит забывать также о постоянном ускорении силы тяжести. Учитывать его нужно даже тогда, когда система остается в покое, а составляющие системы являются объектами воздействия силы тяжести.
Можно сделать предположение, что сила натяжение этой веревки будет рассчитываться по следующей формуле: \(T=(m\times{g})+(m\times{a})\). В данной формуле \(g\) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.
Для решения большей части физических задач предполагается, что веревка идеальна. То есть, она идеально тонкая, у нее нет массы, она не способна рваться и растягиваться.
Рассмотрим пример, в котором груз подвешивается к деревянной балке при помощи одной веревки. Ни веревка, и груз не передвигаются — система в абсолютном покое. Чтобы груз находился в полном равновесии, сила натяжения обязана равняться силе тяжести: \(F_{т}=F_{g}=m\times{g}\). Если у груза масса 10 кг, то сила натяжения будет равна \(98 Н (10\times9,8)\).
Второй этап — нужно учитывать ускорение. Сила тяжести является не единственной силой, которая может повлиять на силу натяжения нити. Ровно такое же действие совершает каждая сила, которую прикладывают к объекту на нити с ускорением.
Если объект, который подвешен на кабеле или веревке, ускоряется под воздействием силы, то к силе натяжения будет добавляться сила ускорения. Представим, что на веревку подвешивают груз с массой в 10 кг, потом тянут вверх с ускорением, которое равно 1 м/с². В данном случае нужно учитывать ускорение груза вместе с ускорением силы тяжести:
\(F=F+(m\times{a})\)
\(F=98+(10\times{1})\)
\(F=108 Н.\)
Третий этап — нужно учитывать угловое ускорение. Тело находится на веревке, которая вращается вокруг определенной точки, ее считают условным центром (по типу маятника). Оно оказывает натяжение на нить при помощи центробежной силы.
Центробежная сила — побочная сила натяжения, вызванная веревкой. Возникает при толчке внутрь веревки таким образом, чтобы груз сохранял свое движение по дуге, а не по прямой. Центробежная сила тем больше, чем быстрее движется объект: \(F=m\frac{v^{2}}{r}.\)
В этой формуле m является массой, v — скоростью, r — радиусом окружности, по которой происходит движение груза.
Так как значение и направление центробежной силы изменяются в зависимости от того, как тело передвигается и изменяет собственную скорость, полное натяжение нити становится параллельным нити в центральной точке.
Важно запомнить, что сила притяжения всегда воздействует на тело, тянет его вниз. Если объект совершает амплитудное действие вертикально, полное натяжение сильнее всего будет в нижней точке дуги (точка равновесия для маятника) — когда тело достигает самой большой скорости, а слабее всего — в верхней точке дуги, когда тело начинает замедляться.
Приведем пример: объект не ускоряется вверх, а раскачивается как маятник. Допустим, что нить будет иметь длину 1,5 м, а груз передвигается со скоростью 2 м/с (в случае прохождения через нижнюю точку размаха). Если необходимо рассчитать силу натяжения в нижней точке дуги (в момент, когда она самая большая), то нужно найти сначала, какое давление силы тяжести ощущает на себе груз в данной точке (в состоянии покоя — 98 Н). Для нахождения центробежной силы нужно применить следующие формулы:
\(F=m\frac{v^{2}}{r}\)
\(F=10\frac{2^{2}}{1,5}\)
\(F=10\times2,67=26,7 Н.\)
Так полное натяжение нити будет \(98+26,7=124,7 Н.\)
Еще одна формула — сила натяжения способна изменяться по мере того, как проходит груз по дуге. Величина и направление центробежной силы изменяются по мере того, как тело качается. Даже если сила тяжести постоянная, результирующая сила натяжения изменяется. В тот момент, когда качающееся тело располагается не в нижней точке дуги, сила тяжести тащит тело вниз, однако сила натяжения тянет тело вверх под углом. По данной причине сила натяжения обязана находиться в противодействии лишь части силы тяжести, а не всей.
Деление силы гравитации на два вектора может помочь визуально показать данное состояние. В каждой точке дуги объекта, который раскачивается вертикально, нить создает угол \(\ominus\) с линией, проходящей через точку равновесия, центр вращения. После того как маятник раскачивается, сила гравитации разделяется на два вектора:
- \(mg\sin\ominus\), воздействует по касательной к дуге по направлению к точке равновесия;
- \(mg\cos\ominus\), воздействует параллельно силе натяжения, однако в ином направлении.
Натяжение имеет возможность противостоять \(mg\cos\ominus\)— только такой силе, которая направлена против нее, а не полноценной силе тяготения (кроме точки равновесия).
Представим пример: маятник имеет отклонение в 15° от вертикали, движение происходит со скоростью 1,5 м/с. Можно найти силу натяжения следующим образом:
- Найдем отношение силы натяжения к силе тяготения: \(Т=98\cos15=98(0,96)=94,08 Н\).
- Найдем центробежную силу: \(F=10\times\frac{1,5^{2}}{1,5}=10\times1,5=15\).
- Полное натяжение будет следующим: \(T + F = 94,08 + 15 = 109,08 Н\).
Еще одна формула — с учетом расчета трения. Каждый объект, который тянут нитью по поверхности, чувствует на себе силу замедления из-за трения, и передает данное воздействие натяжению в нити.
Сила трения между двумя телами рассчитывается, как и в другой любой ситуации, в соответствии со следующим уравнением: \(F=(\mu)N\). В данной формуле \(\mu\) является коэффициентом силы трения между телами, N является силой взаимодействия двух объектов\сила, с которой они воздействуют друг на друга.
Трение покоя — трение, возникающее в итоге попыток привести тело, находящееся в состоянии покоя, в движение.
Трение движения — трение, которое возникает в итоге попыток заставить движущееся тело продолжать это движение.
Приведем пример: представим, что груз в 10 кг не раскачивается, его тянут по горизонтальной плоскости при помощи нити\веревки. Коэффициент трения по земле будет равен 0,5. Груз передвигается со скоростью, которая постоянна, однако нужно придать телу ускорение в 1 м/с².
Нужно сделать следующие расчеты: \(F=10\times9,8 =98 Н.\)
Сила трения будет рассчитана по формуле: \(F=0,5\times98=49 Н.\)
Сила ускорения будет рассчитана по формуле: \(F=10\times1=10 Н\).
Общее натяжение: \(F+F=49+10=59 Н.\)
Нахождение силы натяжения на нескольких нитях
Один из способов нахождения силы натяжения нити — использовать вертикальные параллельные грузы при помощи блока.
Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения веревки.
В обычном расположении блока кабель\нить\веревка начинаются от подвешенного объекта вверх к блоку, потом вниз к иному объекту. Так создаются два разных участка веревки. В таком случае натяжение на всех участках становятся одинаковыми, если оба конца натягиваются силами различных величин.
Для системы масс, подвешенных вертикально в блоке, сила натяжения будет равна \(T=\frac{2g(m1)(m2)}{m2+m1)}\). В данной формуле g будет ускорением силы тяжести, m1 — массой первого тела, m2 — массой второго тела.
Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.
Приведем пример: есть два груза, которые подвешены через блок на параллельных концах нити. Один груз обладает массой в 10 кг, а второй груз обладает массой в 5 кг. В данном случае нужно произвести расчет по следующим формулам:
\(T=\frac{2g(m1)(m2)}{m2+m1)}\)
\(T=\frac{2(9,8)(10)(5)}{5+10)}=\frac{980}{15}=65,33 Н.\)
Важно понимать, что из-за того, что один груз является более тяжелым, другие элементы будут равны, данная система будет ускоряться, значит, груз в 10 кг будет передвигаться вниз, заставляя второй объект идти вверх.
Другая формула — подвешиваем грузы, берем блоки с нитями, которые не параллельны. Блоки часто используют для того, чтобы направить силу натяжения в другую сторону. Если груз подвешивается вертикально к одному концу нити, а другой конец поддерживает груз в диагональной плоскости, то система блоков — непараллельная — формирует треугольную форму с углами в точках с первым грузом, вторым, а также самим блоком. В данном случае натяжение в веревке будет зависеть от силы тяжести, силы натяжения, которая будет параллельная диагональной части нити.
Приведем пример: есть система с объектом в 10 кг, подвешенным вертикально, соединяющимся с грузом в 5 кг, который находится на наклонной плоскости в 60° (нет трения). Для нахождения натяжения в нити нужно составить следующие уравнения:
- Груз, который подвешивают, намного тяжелее, трение не создается, потому что мы знаем, что груз ускоряется вниз. Натяжение в веревке тащит вверх, поэтому объект ускоряется по отношению к силе (равнодействующей) \(F=m1\times{g}-T=98-Т.\)
- Груз на плоскости, которая находится под наклоном, ускоряется вверх. Так как трения нет у данной плоскости, натяжение тянет груз вверх по плоскости, вниз объект тянет собственный вес. Часть силы, которая тянет вниз по наклонной, будет вычисляться как \(mg\sin\ominus\). Можно предположить, что тело ускоряется по отношению к равнодействующей силе: \(F=T-m^{2}(g)\sin60=T-5(9,8)(0,87)=T-42,14\).
- Если сравнять оба уравнения, то получится следующее: \(98-T=T-42,12\). Вычисляем T, получается, что \(2T=140,14. Так T=70,07 \)Н.
Последняя формула — использование нескольких нитей для того, чтобы подвесить тело. Представим, что объект подвешивается на «Y-образной» системе нитей — две нити закрепляются на потолке, встречаются в центральной точке, из которой третья нить идет с объектом. Сила натяжения третьей нити проста — обычное натяжение в итоге действия силы тяжести или же m(g).
Натяжение на других нитях отличается, они обязаны составлять в совокупности силу, которая равна силе тяжести вверх в вертикальном положении, а также равны нулю в обоих горизонтальных направлениях. Однако нужно взять во внимание, что система покоится. Натяжение в нити зависит напрямую от массы подвешенных грузов, а также от угла, на который происходит наклон каждой нити от потолка.
Приведем пример: в системе Y-образной нижний груз обладает массой в 10 кг, подвешивается на двух нитях, угол одной из нитей составляет 30° с потолком. Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:
- По законам тригонометрии, соотношение между T=m(g) и Т1, Т2 будет равно косинусу угла между нитями и потолком. Для натяжения T1 будет \(\cos30=0,87\). Для натяжения T2 будет \(\cos60=0,5\).
- Нужно умножить натяжение в нижней нити на косинус всех углов, чтобы найти общее натяжение. \(T1=0,87\times{mg}=0,87\times10(9,8)=85,26\) Ньютонов. \(T2=0,5\times{mg}=0,5\times10(9,8)=49\) Ньютонов.
Примеры решения задач
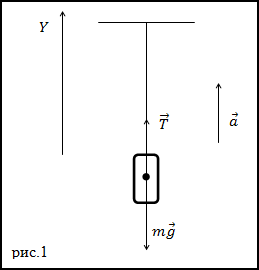
Нерастяжимая, с малым весом нить может выдержать силу натяжения в T=4400 Н. Какое максимальное ускорение может быть, чтобы поднять груз с массой в 400 кг? Груз подвешивают на данную нить. Нужно, чтобы нить при этом не разорвалась, и не произошло падение груза.
На рисунке ниже изображены все силы, которые воздействуют на груз.
Запишем второй закон Ньютона. Объект считается материальной точкой, все силы прикладываются к центру масс объекта: \(T+mg=ma\).
Далее записываем проекции уравнения на ось Y: \(T-mg=ma\).
Получаем уравнение: \(a=\frac{T-mg}{m}\).
Произведем расчеты: \(a=\frac{4400-400\times9,8}{400}=1,2 м/с²\).
Ответ: 1,2 м/с².
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так