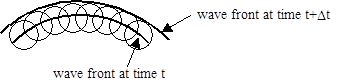Что нужно знать о принципе Гюйгенса Френеля — основные сведения
Принцип Гюйгенса Френеля: формулировка
Принцип Гюйгенса-Френеля — это теория в физике гласящая, что каждая точка на волновом фронте является источником волн, которые распространяются вперед с одинаковой скоростью.
Принцип волнового анализа Гюйгенса в основном гласит, что:
- Каждую точку волнового фронта можно считать источником вторичных волн, которые распространяются во всех направлениях со скоростью, равной скорости распространения волн.
- То означает, что когда у вас есть волна, вы можете рассматривать «край» волны как фактически создающий серию круговых волн. В большинстве случаев эти волны объединяются вместе, чтобы просто продолжить распространение, но в некоторых случаях наблюдаются значительные наблюдаемые эффекты. Волновой фронт можно рассматривать как линию, касательную ко всем этим круговым волнам.
С целью продолжения обсуждения мы должны определить два термина:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Фронт волны — это поверхность постоянной фазы.
- В плоской волне это плоскости, а в сферической волне это сферы. Луч проходит перпендикулярно фронтам.
Значение волнового фронта заключается в том, что это множество или местоположение всех точек в одной и той же фазе. Здесь локус — это путь, пройденный определенной точкой, исходящей от источника света; однако подобных точек миллионы. Все эти точки, проходящие через локус, образуют различные типы волновых фронтов.
Существует три типа волнового фронта, а именно: плоский волновой фронт, сферический волновой фронт и цилиндрический волновой фронт.
В физике периодические волны используются для описания распространения энергии излучения света, звука, ветра или любого другого вида энергии. И поскольку эта волна представляет собой плавное периодическое колебание, она описывается как функция синусоидальных волн.
Христиан Гюйгенс постулировал, что при распространении волны через среду каждая точка на продвигающемся волновом фронте действует как новый точечный источник волны. Это правильная физика для волн воды, но не для световых волн. Однако уравнение Германа Гельмгольца для дифракции электромагнитных волн дает решение, идентичное тому, которое дает принцип Гюйгенса.
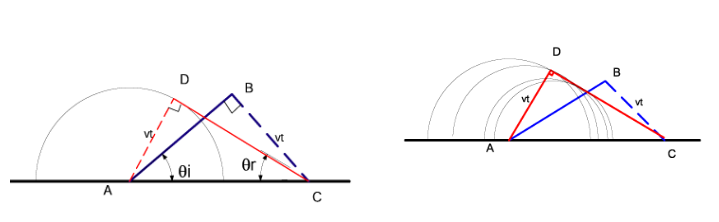
Посмотрите на рисунок, на котором показан волновой фронт AB, выходящий на поверхность и отражающийся, создавая передний CD. Точка А первой попадает на поверхность. Точка B попадает на время vt позже. В течение этого времени сферическая волна испускается из A и проходит расстояние vt. На самом деле это происходит для каждой точки вдоль волнового фронта. На следующем рисунке предпринята попытка показать, как ряд волн выстраивается вдоль линии DC и что она перпендикулярна линии AD.
Из этих иллюстраций мы видим, что:
sinθi = vt/AC
и
sinθr = vt/AC.
Таким образом θi=θr
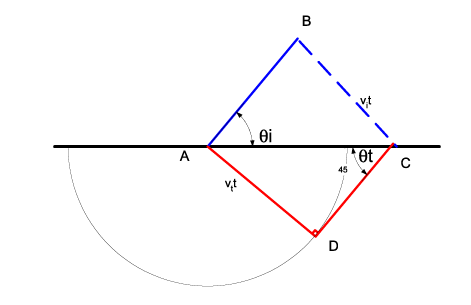
С рефракцией происходит то же самое:
В этом случае скорости в двух средах различны, и поэтому получается:
sinθi = vit/AC
и
sinθt = vtt/AC
который затем может быть изменен на:
sinθi/vit = sinθt/vtt
если преобразовать формулу:
sinθi/sinθt = vit/vtt
или
sinθi/sinθt = nt/ni
наконец получаем формулу:
ntsinθt = nisinθi.
Таков закон Снеллиуса. Обратите внимание, что обычно используются лучи, и в этом случае углы измеряются по нормали к поверхности.
В физике нормаль определяется как перпендикуляр, проведенный к отражающей поверхности.
Суть принципа Гюйгенса-Френеля
В 1678 году великий голландский физик Христиан Гюйгенс (1629-1695) написал трактат под названием «Трактат о свете...» о волновой теории света, и в этой работе он заявил, что волновой фронт распространяющейся волны света в любой момент времени соответствует огибающей сферических волн, исходящих из каждой точки волнового фронта в момент времени. предшествующий момент (при том понимании, что волны имеют ту же скорость, что и общая волна). Иллюстрация этой идеи, ныне известной как принцип Гюйгенса, показана ниже.
На этом рисунке изображено распространение «фронта» волны, но принцип Гюйгенса, как предполагается, одинаково применим к любому участку постоянной фазы (не только к переднему краю возмущения), все они распространяются с одинаковой характерной скоростью волны. Это означает, что волна не становится «толще» по мере ее распространения, т.е. диффузии волн не происходит.
Например, если мы включим лампочку на одну секунду, кто-то, наблюдающий за лампочкой с расстояния в милю, увидит, что она «включена» ровно на одну секунду, и не дольше. Точно так же тот факт, что мы видим четкие изображения далеких звезд и галактик, объясняется принципом Гюйгенса. Однако стоит отметить, что этот принцип действует только в пространствах с нечетным числом измерений.
Если мы бросим камешек в спокойный пруд, круговая волна на двумерной поверхности пруда будет распространяться наружу, и если бы принцип Гюйгенса действовал в двух измерениях, мы бы ожидали, что поверхность пруда будет совершенно спокойна как снаружи, так и внутри расширяющейся сферической волны. Но на самом деле поверхность пруда внутри расширяющейся волны (в этом двумерном пространстве) не совсем спокойна, ее состояние продолжает незначительно отличаться от состояния покоя даже после прохождения основной волны. Это возбужденное состояние будет сохраняться бесконечно, хотя величина быстро становится чрезвычайно малой. То же самое происходит в пространстве с любым четным числом измерений. Конечно, передний край волны всегда распространяется с характерной скоростью c, независимо от того, верен принцип Гюйгенса или нет. В некотором смысле принцип Гюйгенса более важен из-за того, что он говорит о том, что происходит за передним краем возмущения. По сути, он постулирует то, что все фазы распространяются с одинаковой скоростью.
Из этого простого принципа Гюйгенс смог вывести законы отражения и преломления.
Известно, что свет ведет себя очень предсказуемым образом. Если бы можно было наблюдать, как луч света приближается и отражается от плоского зеркала, то поведение света при его отражении подчинялось бы предсказуемому закону, известному как закон отражения.
В физике отражение определяется как изменение направления волнового фронта на границе раздела двух различных сред, отражающее волновой фронт обратно в исходную среду. Распространенным примером отражения является отраженный свет от зеркала или неподвижной лужи воды, но отражение влияет на другие типы волн, помимо света. Также могут отражаться волны воды, звуковые волны, волны частиц и сейсмические волны.
Преломление — это изгиб пути световой волны при ее прохождении через границу, разделяющую две среды. Преломление вызвано изменением скорости, испытываемой волной, когда она меняет среду.
Однако этот принцип несовершенен в том смысле, что он не учитывает направленность распространения волны во времени, т.е. он не объясняет, почему фронт волны в момент времени t + Δt на приведенном выше рисунке является верхним, а не нижним огибающим вейвлетом.
Почему расширяющаяся сферическая волна продолжает расширяться наружу от своего источника, вместо того, чтобы снова сходиться внутрь обратно к источнику? Кроме того, принцип, первоначально сформулированный Гюйгенсом, не учитывает дифракцию. Впоследствии Огюстен Френель (1788-1827) развил принцип Гюйгенса, заявив, что амплитуда волны в любой заданной точке равна суперпозиции амплитуд всех вторичных волн в этой точке (при том понимании, что волны имеют ту же частоту, что и исходная волна). Принцип Гюйгенса-Френеля адекватен для объяснения широкого спектра оптических явлений, и позже Густав Кирхгоф (1824-1887) показал, как этот принцип может быть выведен из уравнений Максвелла. Тем не менее (и, несмотря на утверждения об обратном в литературе), это фактически не решает вопрос об «обратном» распространении волн, поскольку сами уравнения Максвелла теоретически допускают как опережающие, так и запаздывающие потенциалы. Принято просто сбрасывать со счетов продвинутые волны как «нереалистичные» и относиться к замедленной волне так, как если бы это было уникальное явление.
Действительно ли мы сейчас нашли истинную причину поведения света, является спорным.
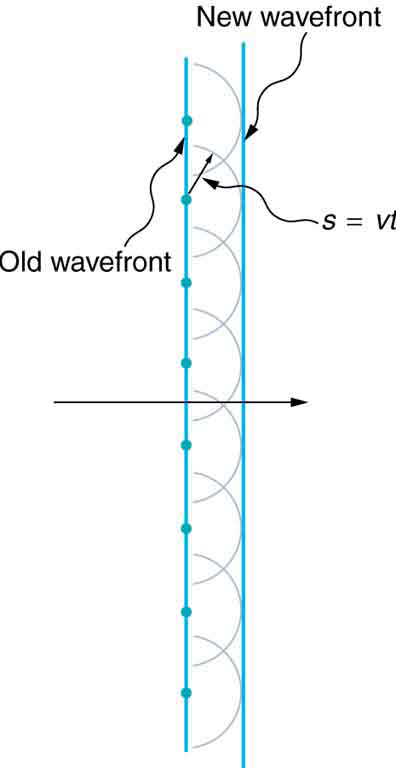
Прямой волновой фронт: принцип Гюйгенса, применяемый к прямому волновому фронту. Каждая точка на волновом фронте испускает полукруглый вейвлет, который перемещается на расстояние s=vt. Новый волновой фронт представляет собой линию, касательную к вейвлетам.
На рисунке выше показан простой пример принципа дифракции Гюйгенса. Принцип можно показать с помощью приведенного ниже уравнения:
s=vt,
где s — расстояние, v — скорость распространения, а t — время.
Каждая точка на волновом фронте испускает волну со скоростью, v. Излучаемые волны имеют полукруглую форму и возникают через t, время позже. Новый волновой фронт является касательным к вейвлетам. Этот принцип работает для всех типов волн, а не только для световых волн. Принцип полезен при описании отражения, преломления и интерференции. наглядно показывает, как принцип Гюйгенса может быть использован для объяснения отражения, и показывает, как его можно применить к преломлению.
Принцип волнового анализа Гюйгена помогает понять движение волн вокруг объектов, их положение. Поведение волн иногда может быть нелогичным. Легко думать о волнах так, как будто они просто движутся по прямой линии, но у нас есть веские доказательства того, что это часто просто неверно.
Например, если кто-то кричит, звук распространяется во всех направлениях от этого человека. Но если они находятся на кухне с одной дверью и кричат, волна, направляющаяся к двери в столовую, проходит через эту дверь, но остальная часть звука ударяется о стену. Если столовая имеет Г-образную форму, а кто-то находится в гостиной, которая находится за углом и через другую дверь, они все равно услышат крик. Если бы звук двигался по прямой линии от человека, который кричал, это было бы невозможно, потому что звук не мог бы переместиться за угол.
Что объясняет принцип Гюйгенса-Френеля
В физике периодические волны используются для описания распространения энергии излучения света, звука, ветра или любого другого вида энергии. И поскольку эта волна представляет собой плавное периодическое колебание, она описывается как функция синусоидальных волн. В прежние времена свет описывался как комбинация очень крошечных частиц, которые не имеют никакой массы. Также было выдвинуто предположение, что частицы света разного цвета также различны. Все другие природные явления света, такие как отражение, преломление, дифракция, были поняты на основе этой гипотезы и с учетом того, что частицы света эластичны по своей природе.
В XVII веке Христиан Гюйгенс совершил научную революцию. Он предположил, что свет на самом деле является формой энергии и движется в форме волн. Он объяснил это предположением, что любой точечный источник света излучает световые волны во всех направлениях одновременно в трех измерениях. Сущность его теории заключается в том, что частицы в его окружении периодически вибрируют под воздействием волновой энергии. При этом типе распространения точки определенного местоположения присутствуют в одной и той же фазе по времени. Плоскость, образованная этим расположением точек или частиц в одной и той же фазе, известна как волновой фронт.
Использование зон Френеля для расчета амплитуды волны
Зона Френеля, названная в честь физика Огюстена-Жана Френеля, представляет собой одну из серии конфокальных вытянутых эллипсоидальных областей пространства между передатчиком и приемником и вокруг них.
Первичная волна будет проходить по относительной прямой линии от передатчика к приемнику. Аберрантные передаваемые радиоволны, звуковые или световые волны, которые передаются одновременно, могут следовать по несколько разным путям, прежде чем достичь приемника, особенно если между ними есть препятствия или отклоняющие объекты. Две волны могут поступать на приемник в несколько разное время, и отклоняющаяся волна может поступать не по фазе с основной волной из-за разной длины пути. В зависимости от величины разности фаз между двумя волнами волны могут создавать конструктивные или разрушительные помехи. Размер рассчитанной зоны Френеля на любом конкретном расстоянии от передатчика и приемника может помочь предсказать, будут ли препятствия или разрывы вдоль пути вызывать значительные помехи.
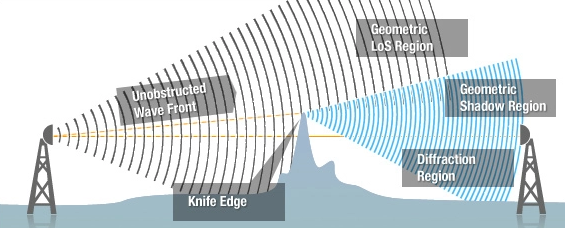
Обсуждение зоны Френеля довольно сложное, но концепции должны быть довольно простыми для понимания. Есть несколько явлений, которые нужно понять, первое — это волновые принципы Гюйгенса, которые гласят, что волны начнут образовывать новые круговые волны в каждой точке волнового фронта. Проще говоря, если волна попадает в точку объекта в пространстве, круговые волны будут рассеиваться наружу и вперед полукруглым образом, как показано на диаграмме ниже:
Изображение дифракции волн
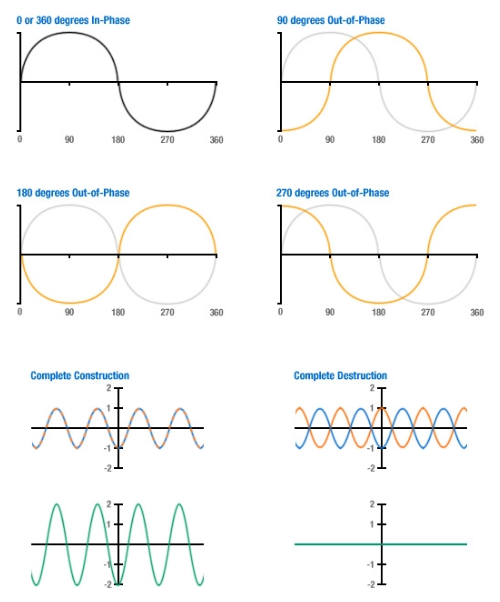
Во-вторых, все лучи радиочастотного сигнала расширяются по мере распространения по воздуху; угол, под которым они расширяются, может быть ограничен направленными антеннами. Наконец, сигналы могут мешать друг другу, особенно на одинаковых частотах, из-за того, что волны не совпадают по фазе друг с другом. Этот фазовый сдвиг вычисляется между 0 и 360 градусами, при этом полное совпадение по фазе происходит при 0 и 360 градусах, а полное смещение по фазе — при 180 градусах. Волны накладываются друг на друга, и те, которые находятся в фазе, подвергаются конструктивным помехам, при этом амплитуда их сигнала складывается вместе, чтобы создать более сильный сигнал, но сигналы вне фазы испытывают разрушительные помехи, снижающие усиление сигнала до точки полного уничтожения, если они идентичны, но на 180 градусов не совпадают по фазе. Это может быть легче понять визуально, как показано на диаграммах ниже:
Сдвиг фазы волн
Теория зон Френеля использует прямую линию между двумя работающими беспроводными сетевыми устройствами с точками A и B на каждом конце, а также трехмерное пространство вокруг линии, которое влияет на сигнал, поступающий на принимающий конец. Часть сигнала проходит непосредственно по пути от A до B, в то время как другие волны отклоняются от этой прямой линии по траекториям вне оси, что приводит к тому, что их пути передачи имеют большее расстояние, вызывая сдвиг фазы между этими различными лучами. Путем введения понятий, объясненных выше, и применения некоторых вычислений было обнаружено, что вокруг прямого пути AB расположены эллипсоидальные кольцевые зоны, которые влияют на уровень сигнала, воспринимаемого приемником.
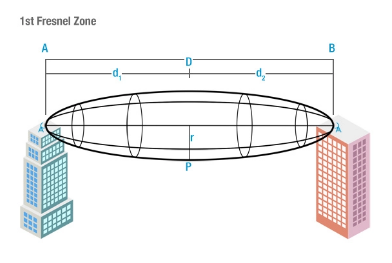
Существует бесконечное количество вычисляемых зон Френеля, но зона Френеля, которая оказывает наибольшее влияние на производительность беспроводной сети, — это 1-я зона Френеля. Если в этой 1-й зоне Френеля есть какие-либо препятствия, такие как здания, деревья или холмы, они будут влиять на сигнал и, следовательно, будут ослаблены на приемнике. Как правило, при планировании беспроводных линий связи 1-я зона Френеля всегда должна быть свободна от препятствий, но это может быть непрактично, поэтому говорится, что не более 40% должно быть заблокировано, т.е. очищено на 60%, но рекомендуется, чтобы для оптимальной производительности оно было заблокировано не более чем на 20% или менее. Обратите внимание, что препятствия в 1-й зоне Френеля будут создавать сигналы, которые будут отклоняться от фазы на 0-90 градусов, от 90 до 270 градусов по фазе во второй зоне, от 270 до 450 градусов по фазе в третьей зоне и т.д.
Диаграмма зон Френеля
Чтобы рассчитать зоны Френеля для вашей беспроводной сети, сначала установите RF Los (Линию прямой видимости), которая представляет собой прямую прямую линию между антеннами передатчика и приемника (или приемопередатчиков). Общее уравнение для вычисления радиуса зоны Френеля в любой точке P между конечными точками беспроводной линии связи может быть показано следующим уравнением:
Fn = sqrt((n*λ*d1*d2)/(d1+d2))
Где,
Fn = N-й радиус зоны Френеля (м);
d1 = Â Расстояние P от точки A (м);
d2 = Â Расстояние P от точки B (м);
λ = Â Длина волны сигнала (м).
Радиус Зоны Френеля имеет наибольшее значение (наибольшее расстояние) непосредственно в центре радиочастотной зоны, и для практического применения планирования беспроводных сетей полезно знать максимальный радиус 1-й зоны Френеля.
Следовательно, расстояния между точками A и B до P будут одинаковыми, и, преобразовав значение длины волны в частоту сигнала, мы можем сказать следующее:
λ = c/f d1 = D2, следовательно, d1 + d2 = D.
Где,
c = Скорость света в вакууме (3x108 мс-1);
D = Â Общее расстояние (м);
f = Â Частота сигнала (Гц).
Следовательно, если значения частоты и общего расстояния преобразуются в ГГц и км соответственно, уравнение для максимального радиуса 1-й зоны Френеля может быть получено следующим образом:
r = 8,657*sqrt(D/f).
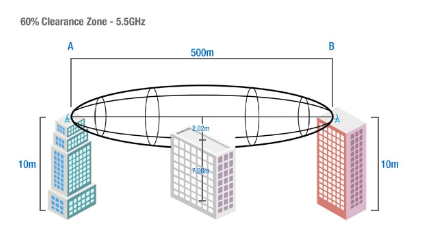
При расчете максимального радиуса 1-й зоны Френеля 500-метровой линии связи, работающей на частоте 5,5 ГГц (5 ГГц 802.11n канал 100):
r = 8,657*sqrt(0,5/5,5) = 2,61.
Если бы антенны для двух устройств были расположены на высоте 10 м над землей (при условии, что оба местоположения находятся на одинаковой высоте над уровнем моря), 1-я зона Френеля проходила бы на высоте 7,39 м над землей в самом широком месте.
Для вычисления радиуса зоны Френеля с прозрачностью 60% необходимо использовать следующее уравнение:
r = 8,657*sqrt((0,6D)/f).
Итак, для нашего примера это будет рассчитываться как:
r = 8,657*кв.м((0.6*0.5)/5.5) = 2.02 м.
Вычитая эту цифру из высоты антенны, вы можете рассчитать максимальную высоту любого препятствия между устройствами в пределах 60% чистой зоны Френеля.
Максимальная высота препятствия = 10 - 2,02 = 7,98 м.
60% Зона Френеля
Следовательно, максимально допустимая высота любого препятствия, расположенного в пределах радиочастотной зоны между двумя устройствами, на расстоянии 500 м друг от друга, работающего на частоте 5,5 ГГц, при высоте антенны 10 м с минимальным зазором Зоны Френеля 60%, составляет 7,98 м.
Для линий связи, которые перемещаются на большие расстояния (особенно более 1 км), следует учитывать кривизну Земли. Поскольку поверхность Земли изгибается, выпуклость между двумя звеньями (более технически область между хордой, образованной между двумя устройствами) сама по себе становится препятствием зоны Френеля и может препятствовать зонам Френеля, даже если нет других очевидных препятствий.
Формула для расчета влияния радиуса Земли выглядит следующим образом:
H = (1000*D^2)/(8*Er)
Где,
H = Разность высот кривизны Земли в средней точке между двумя устройствами (м);
D = Â Общее расстояние связи между двумя устройствами (км);
Er = Эффективный радиус Земли (км).
Обычно принимается за 4/3 (1,333 рек.) фактического радиуса для учета атмосферной рефракции, т.е. 8504 км.
При расчете максимальной разницы в высоте из-за кривизны Земли между двумя устройствами, расположенными на расстоянии 5 км друг от друга:
H = (1000*5^2)/(8*8504) = 0.37 м.
Таким образом, вы можете видеть, что на расстоянии 5 км Земля поднимается на 0,37 м в своей максимальной точке из-за своей кривизны, и это может быть учтено при планировании для обеспечения оптимальной производительности. Самое простое решение для решения этой проблемы — поднять антенны обоих устройств, чтобы увеличить зону Френеля.
Диаграмма припуска кривизны Френеля
Ниже приведена небольшая таблица, показывающая допуски, которые необходимо сделать из-за кривизны Земли на различных расстояниях:
| Расстояние связи (км) | Допуск на кривизну (м) |
| 1 | Незначительный |
| 2 | Незначительный |
| 3 | 0,2 |
| 5 | 0,4 |
| 10 | 1,5 |
| 15 | 4 |
| 20 | 6 |
| 25 | 10 |
| 30 | 13 |
| 35 | 18 |
| 40 | 24 |
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так