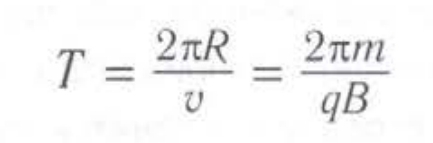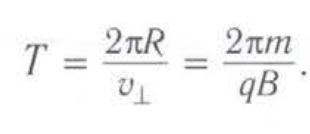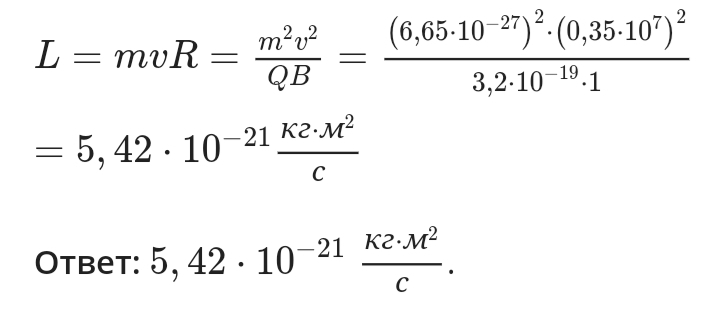Как пользоваться правилом правой и левой руки

Правило правой и левой руки в физике 

В XIX веке ученые обнаружили, что между магнетизмом и электричеством есть связь. В это же время сформировалось понятие магнитного поля, впервые обнаруженное датским ученым-физиком Х. Эрстедом. После этого открытия различные ученые, проводя эксперименты, установили широкий спектр действия поля, зачастую выходящий за рамки исследуемого объекта, а также его круговое вращение.

В дальнейшем было установлено направление действия магнетизма и разносторонность его влияния, которое меняется от расположения полюса и силы, оказывающих влияние на проводник.

По результатам экспериментов были сформированы правила левой и правой руки. С помощью первого выявляют направленность сил, влияющих на проводящий материал, а при помощи второго — направленность магнитных линий.

С целью наглядности были приняты специальное определение и другие обозначения. Поле изображается в виде концентрических линий. Сила действующего поля тем выше, чем чаще они расположены относительно друг друга. Каждая из них получается замкнутой и параллельной с соседними.

Если известно их направление, становится известной направленность вектора магнитной индукции и наоборот. Потому что направление вектора будет соприкасаться с каждой точкой этих линий.

Что определяет правило левой руки

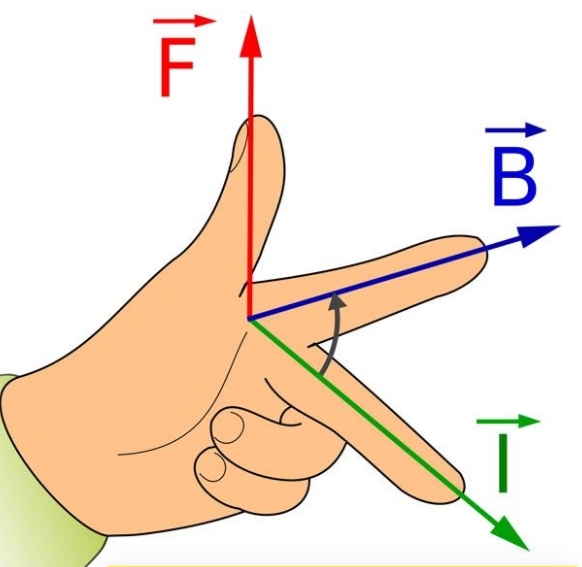
Сила Ампера F_A всегда перпендикулярна направлению тока в проводнике и вектору индукции \[\bar{B}\] магнитного поля. Для определения направления силы Ампера используют правило левой руки:

Интерпретация для точечного заряда

Согласно закону Ампера на проводник с током в магнитном поле действует сила, рассматриваемая как результат действий магнитного поля на все существующие в проводнике заряды. Можно сделать вывод, что магнитное поле действует с силой на все движущиеся заряды.

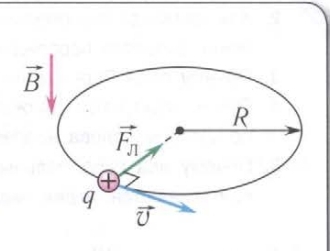
Выражение для силы, с которой магнитное поле действует на движущийся заряд, впервые вывел голландский физик Хендрик Антон Лоренц в 1985 году: F_л = qυB sin α. В его честь эта сила называется силой Лоренца. 

Направление силы Лоренца определяется правилом левой руки:

Для отрицательно заряженной частицы (например, для электрона) направление силы будет противоположным.

Еще один вариант определения силы Лоренца:

Применение на практике, формула

Сила Лоренца из-за перпендикулярности вектору скорости не изменяет модуль скорости, а может изменить только ее направление. Значит, сила Лоренца работы не совершает. Отсюда следует вывод: при однородности поля и при движении частицы перпендикулярно к магнитной индукции поля, ее траектория будет описывать окружность, плоскость которой перпендикулярна магнитному полю. 

Ускорение частицы a = υ²/R (R — радиус окружности) направлено к центру окружности. Используя второй закон Ньютона, можно найти период обращения частицы по окружности. 

Радиус окружности, описываемой частицей в магнитном поле: R = (mυ)/(qB). 

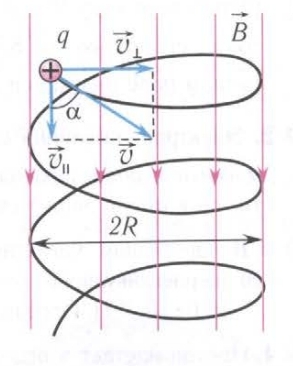
При направлении скорости к индукции магнитного поля под углом, движение заряда можно представить в виде двух независимых движений:

• равномерного вдоль поля υ_|| (υ_|| — составляющая вектора скорости, параллельная вектору индукции B магнитного поля);
• по окружности радиусом R в плоскости, перпендикулярной вектору B, с постоянной по модулю скоростью υ_⊥ (υ_⊥ — составляющая вектора скорости, перпендикулярная вектору индукции B магнитного поля).

После сложения обоих движений возникнет движение по винтовой линии, ось которой параллельна магнитному полю.

Период этого движения определяется по формуле:

Правило буравчика для правой руки 

Джеймсом Клерком Максвеллом было предложено правило буравчика для определения направления вектора индукции магнитного поля прямого тока:

Описание простым языком

Для определения направления линий индукции магнитного поля прямолинейного проводника с током используется правило обхвата правой руки:

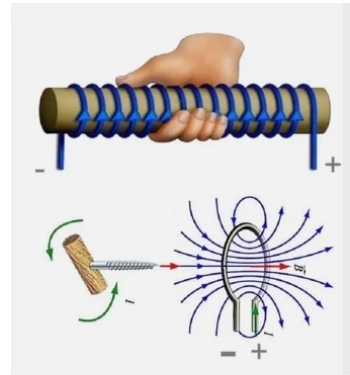
Сформулированные алгоритмы применимы и для катушек с током. Но в таком случае будет разница во вращении рукоятки буравчика таким образом, чтобы это движение совпадало с направлением токов в витках. При этом продвижение винта буравчика будет указывать на ориентацию вектора магнитных линий в соленоиде.

При охвате правой рукой (условно) катушки так, чтобы направление тока в витках совпадало с пространственным расположением пальцев, большой палец будет указывать ориентацию вектора электромагнитных линий внутри катушки.

Формула для произведения векторов

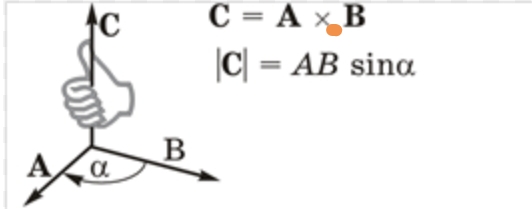
1. Если согнуть пальцы правой руки и направить в сторону кратчайшего пути с целью совместить вектор-сомножитель с другим сомножителем (векторы выходят из одной точки), то по отведенному в сторону большому пальцу можно определить направление аксиального вектора.
2. Если правую ладонь расположить таким образом, чтобы получилось совпадение большого пальца с первым вектором-сомножителем, а указательного — со вторым, то отведенный в сторону средний палец совпадет с направлением вектора произведения.

 Для базисов

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве тесно взаимосвязаны.

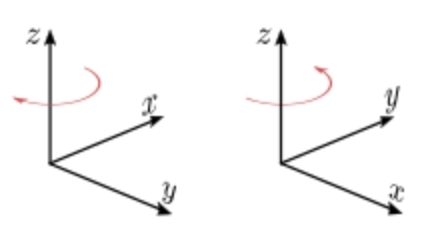
Левая и правая (на рисунке соответственно слева и справа) декартовы системы координат (левый и правый базисы) считаются положительными. Принято использовать по умолчанию правый (это общепринятое соглашение; но при явной оговорке особых причин возможно отойти от него). 

Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис. 

Примеры решения задач по электротехнике