Понятие материальной точки

Материальная точка — это

В механике, когда анализируют движение тела или пытаются выяснить, как оно ведет себя под действием сил, принято делать определенные допущения, чтобы упростить анализ. Если размеры анализируемого тела не оказывают существенного влияния на описание движения или на действие сил на него, то его размерами можно пренебречь в анализе. В этом случае объект моделируется как материальная точка. Например, если смотреть на объект с достаточно большого расстояния, то объект конечного размера выглядит и ведет себя как материальная точка.

Эта модель не работает, когда форма и размер влияют на движение, например, под действием силы сопротивления воздуха.

Момент инерции материальной точки

Общая формула для нахождения момента инерции любого объекта такова:

I = mr2

где: m — масса объекта, r — расстояние от оси вращения.

Момент инерции системы частиц задается формулой:

I = ∑m_ir_i²

где: r_i — перпендикулярное расстояние i-й частицы от оси, m_i — масса первой частицы.

Приведенное выше уравнение момента инерции говорит о том, что момент инерции для системы частиц равен сумме произведения массы каждой из них и квадрата расстояния от оси вращения каждой частицы.

Момент инерции любого объекта зависит от следующих величин:

1. Форма и размер объекта.
2. Плотность материала, из которого изготовлен объект.
3. Ось вращения.

Импульс

Это произведение массы и скорости объекта. Это означает, что импульс прямо пропорционален как массе, так и скорости. Чем больше масса объекта, тем больше его импульс. Аналогично, чем больше скорость, тем больше импульс у объектов, которые движутся быстрее.

Импульс объекта также может меняться при изменении его движения.

Единицы импульса определяются из уравнения импульса и того факта, что импульс — это произведение массы и скорости. Стандартными единицами массы являются килограммы (кг), а единицами скорости — метры в секунду (м/с). Поэтому импульс измеряется в единицах кг⋅м/с.

Векторы — это величины, которые имеют как величину, так и направление. Скорость является векторной величиной, потому что показывает, как быстро движется объект и в каком направлении он движется, например, 25 м/с на восток. Поскольку импульс зависит от скорости, он также является вектором.

Уравнение для импульса:

p=mv
где: p — импульс, m — масса, v — скорость.

Увидеть импульс в действии и рассчитать его можно в различных экспериментах. Чтобы рассчитать импульс объекта в эксперименте, вам понадобятся весы для измерения массы объекта, линейка для измерения расстояния и секундомер для измерения времени. Измерив расстояние и время, которое проходит объект, можно рассчитать его скорость по формуле:
v=d/t.

Кинематика

Находит свое применение в астрофизике для изучения движения небесных объектов. Она также используется в робототехнике и биомеханике для объяснения движения объектов с сочлененными частями, таких как двигатели, человеческие скелеты, роботизированные руки и многое другое. В кинематике мы изучаем траектории движения объектов, а также их дифференциальные свойства, такие как скорость и ускорение.

Системы отсчета

Чтобы понять движение объекта, необходимо описать его положение относительно системы отсчета. Математически для представления положения объекта используется переменная x. Переменная положения x может быть описана двумя способами. Мы можем решить, где поставить x = 0 и какое направление принять за положительное. Это называется выбором системы отсчета или системы координат. Таким образом, выбор системы координат или набора осей, в пределах которых измеряются положение, ориентация и другие свойства объекта, называется системой отсчета.

Перемещение

Изменение положения объекта относительно системы отсчета называется перемещением. Например, если человек идет от своего дома до рынка, то смещение — это относительное расстояние рынка от его дома (системы отсчета).

Скорость и ускорение
Скорость объекта определяется как отношение перемещения к затраченному времени. Она является векторной величиной и имеет как величину, так и направление. Скорость изменения скорости называется ускорением.

График движения
В кинематике изучаются три типа графиков движения:

1. График перемещения-времени.
2. График скорости-времени.
3. График ускорения-времени.

Диаграмма движения

Изображение движения объекта называется диаграммой движения. На одной и той же диаграмме изображаются различные положения объекта через равные промежутки времени. По диаграмме можно понять, ускорился ли объект, замедлился или находится в состоянии покоя. Мы можем понять, что объект ускоряется, если с течением времени пространство между объектами увеличивается, и объект замедляется, если пространство между объектами уменьшается со временем.

Кинематические уравнения

Существует четыре кинематических уравнения, когда в качестве начальной точки отсчета берется начало координат, а ускорение объекта постоянно.

1. v = v0 + at
2. d = (½) (v0 + v)t
3. d = v0t + (at2/2)
4. v2 = v02 + 2ad

где:

v — конечная скорость, a — постоянное ускорение, d — перемещение, v0 — начальная скорость, t — интервал времени.

В каждом из приведенных выше уравнений есть только четыре из пяти переменных. Если мы знаем значение трех переменных в уравнении, то четвертую переменную можно определить.

Уравнения кинематики вращательного движения

В поступательном движении, как мы видели, есть пять важных переменных. Каждая из этих переменных будет иметь соответствующую переменную во вращательном движении. При вращательном движении переменная положения x заменяется углом θ. Начальная и конечная скорость задается угловой скоростью (ω) и измеряется в радианах в секунду. Ускорение заменяется угловым ускорением (α), которое описывает скорость изменения угловой скорости по отношению ко времени. Угловое ускорение измеряется в радианах в секунду в квадрате. Даже при вращательном движении время представляется как t. Уравнения кинематики вращательного движения выглядят следующим образом:

1. ω = ω0 + αt
2. θ = θ0 + (½) (ω0 + ω)t
3. θ = θ0 + ω0t + (αt2/2)
4. ω 2 = ω02 + 2α (θ - θ0)

Динамика

Используются принципы Ньютона, законы сохранения энергии и импульса, а также другие фундаментальные законы механики. В конце 1600-х годов Исаак Ньютон выдвинул гипотезу, что движение не требует причины, скорее изменения в движении требуют причины. Динамика материальной точки является ключевым компонентом в теоретическом и практическом изучении механики и физики в целом, и на практике используется для анализа и прогнозирования движения различных объектов, начиная от мельчайших частиц и заканчивая космическими аппаратами.

Ньютон описал взаимосвязь между силами и движением с помощью трех основных принципов.

Первый закон

Первый закон движения, также известный как закон инерции, можно кратко сформулировать следующим образом: Объект в состоянии покоя остается в состоянии покоя, а объект в движении остается в движении, с постоянной скоростью и по прямой линии, если на него не действует чистая сила.

Это означает, что если на объект не действует чистая (неуравновешенная) сила, то объект будет продолжать свое движение с постоянной скоростью. Если эта скорость равна нулю (объект находится в состоянии покоя), то объект будет продолжать оставаться в состоянии покоя. Если эта скорость не равна нулю, объект будет продолжать двигаться по прямой с той же скоростью. Однако если на объект действует чистая (неуравновешенная) сила, его скорость изменится (он ускорится).

Второй закон

2-й закон движения — возможно, самый важный принцип во всей современной физике, поскольку он объясняет, как именно изменяется скорость объекта под действием чистой силы. Гласит: Ускорение объекта прямо пропорционально приложенной силе и обратно пропорционально массе объекта.

Важно помнить, что и сила, и ускорение — это векторы. Поэтому направление ускорения, или изменения скорости, будет совпадать с направлением чистой силы. Можно посмотреть на это уравнение с противоположной точки зрения. Чистая сила, приложенная к объекту, изменяет его скорость (создает ускорение) и часто записывается в виде: F→ =ma→.

Третий закон

3-й закон движения, обычно называемый законом действия и реакции, описывает явление, при котором все силы действуют парами. Если объект 1 оказывает силу на объект 2, то объект 2 должен оказывать обратную силу на объект 1. Причем сила воздействия объекта 1 на объект 2 равна по величине, или размеру, но противоположна по направлению силе воздействия объекта 2 на объект 1.

→FAB=−→FBA

Закон движения

Когда для описания движения точки требуется только одна координатная ось и время, говорят, что она находится в линейном или прямолинейном движении. Примерами линейного движения являются парад солдат, поезд, движущийся по прямой линии, и многие другие. Важными параметрами, необходимыми для изучения движения по прямой, являются положение, перемещение, скорость и ускорение.

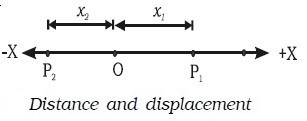
Движение частицы можно описать, если ее положение известно непрерывно относительно времени. Общая длина пути — это расстояние, пройденное частицей, а кратчайшее расстояние между начальным и конечным положением частицы — ее перемещение.
Однако расстояние, пройденное частицей, отличается от ее смещения от начала координат. Например, если частица перемещается из точки O в положение P1, а затем в положение P2, ее перемещение в положении P2 равно — x2 от начала координат, но расстояние, пройденное частицей, равно x1+x1+x2 = (2×1+x2).

Источник: engineersfield.com

Пройденное расстояние — это скалярная величина, а перемещение — векторная величина.

Существует три типа прямолинейного движения:

1. Равномерное прямолинейное движение: Когда объект движется с постоянной скоростью с нулевым ускорением, это называется равномерным прямолинейным движением.
2. Равномерно ускоренное прямолинейное движение: Когда объект движется с постоянным ускорением, это называется равномерно ускоренным прямолинейным движением.
3. Прямолинейное движение с неравномерным ускорением: Когда объект движется с неравномерной скоростью и ускорением, это называется прямолинейным движением с неравномерным ускорением.