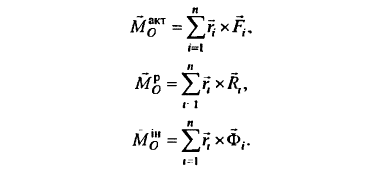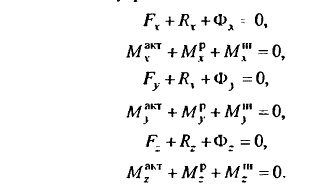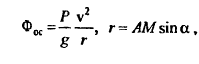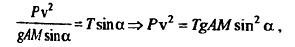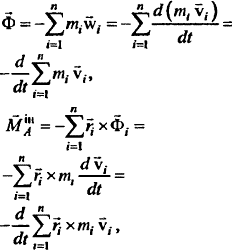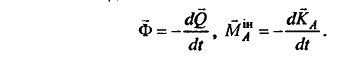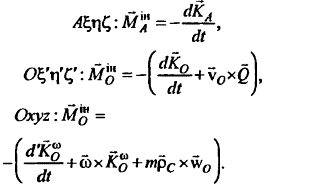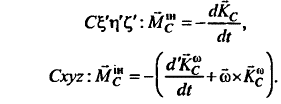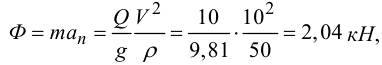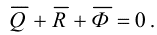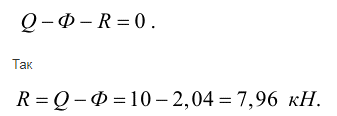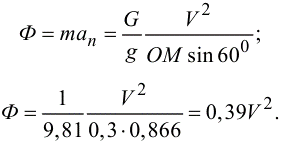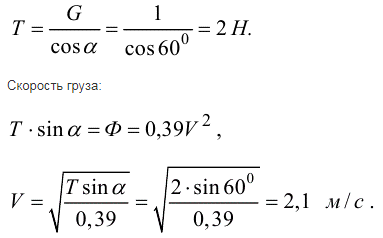Что нужно знать о принципе Даламбера — основные сведения
- Метод кинетостатики в динамике. Формулировка принципа Даламбера
- Формула для принципа
-
Применение принципа Даламбера
- Принцип невесомости
- Принцип невозмущенности математического маятника
- Принцип Даламбера для системы материальных точек
- Расчет инерционных сил материальной точки
- Расчет основного вектора, а также основного момента сил инерции для твердого объекта
- Инерционная сила Даламбера
- Где используют принцип Даламбера
- Пример решения задачи с использованием принципа Даламбера
Метод кинетостатики в динамике. Формулировка принципа Даламбера
Кинетостатика — раздел теории механики, в рамках которого рассматривают варианты решения динамических задач при помощи графических и аналитических статических методов. В базе кинетостатики заложен принцип Д’Аламбера. Данный принцип гласит, что возможно составить уравнения движения тел в виде статичных уравнений, при условии, что к силам, которые воздействуют на тело, а также реакциям связей добавляются силы инерции.
Жан Лерон Д’Аламбер является французским ученым. Им был сформулирован принцип Д’Аламбера, который сводил динамику к статике. Занимался колебанием струн, гидродинамикой и другими научными областями. Основал раздел изучения гидродинамики.
Так выглядел Д’Аламбер:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Методы кинетостатики
Для того, чтобы решить базовую задачу динамики несвободной физической точки при условии заданного движения и необходимости вычислить силу, применяют методы кинетостатики. Эффективнее всего применять данных метод в случаях, когда необходимо вычислить реакцию связи при условии активных сил, а также законе движения материальной точки.
Законы, которые установил в 17-18 веке Исаак Ньютон, относились к процессу движения свободной материальной точки. Если к данному закону прибавить аксиому об освобождении от связей, тогда нужно будет исследовать не вопросы движения несвободной материальной точки, а вопросы движения свободной материальной точки, на которую влияют активные силы и реакции связей.
Принцип Даламбера можно назвать сопоставимым с вторым законом Исаака Ньютона, а также с аксиомой об освобождении от связей. В механике принято называть данный принцип принципом Даламбера. Однако намного правильнее с теоретической точки зрения было бы дать ему название принципа Германа-Эйлера-Даламбера. Все потому, что все три ученых занимались описанием процесса, описанного в принципе. Петербургский ученый Я. Герман занимался описанием принципа в 1716 году, Л. Эйлер занимался описанием в 1737 году, а Ж. Даламбер занимался описанием в 1763 году.
Л. Эйлером был обобщенный данный принцип намного раньше, чем это сделал Даламбер. Однако Л. Эйлер обобщил данный принцип для установления колебаний гибких тел. Ж. Даламбером в теоретической работе «Трактат о динамике» был описан метод, при помощи которого можно было решать задачи на динамике по принципу статики.
Принцип Даламбера — один из основных динамических принципов, который обуславливает формирование сбалансированной общности сил в случае добавления инерционной силы к активным силам, воздействующим на точки механической системы, а также реакциям связей. Если говорить проще, то получается, что в процессе сложения воздействующих на тело сил, силы инерции и реакции связи, результатом сложения будет ноль.
Сущность принципа Даламбера может формулироваться так: если к активной силе, которая влияет на тело, добавляют инерционную силу, такое тело будет находиться в равновесном состоянии. При этом суммарная величина всех воздействующих в системе сил, которое дополняется вектором инерции, примет нулевую величину. То есть все должно сводиться к нулю.
Принцип Даламбера может применяться в различных сферах науки, в том числе в рамках научных дисциплин (например, сопромат).
Формула для принципа
В форме математической записи принцип Д’Аламбера будет выглядеть так:
\(F_{i}+N_{i}+J_{i}=0\)
В данной формуле i является точкой, на которую влияют силы F. Эти силы были наложены реакциями связи N. В этой формуле также учитываем силу инерции J.
Применение принципа Даламбера
Принцип Даламбера в случае применения к материальной точке. Принцип невесомости. Принцип невозмущенности математического маятника
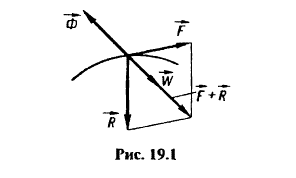
Представим, что на какую-то физическую точку влияет активная сила \(\overrightarrow{F}\), а также реакция связи \(\overrightarrow{R}\). В таком случае, по всем законам уравнений динамики для несвободной физической точки, получится следующее уравнение: \( m\overrightarrow{w}=\overrightarrow{F}+\overrightarrow{R}\). Из этого уравнения получаем: \(\overrightarrow{F}+\overrightarrow{R}+(-m\overline{w})=0\).
Посмотрите на рисунок ниже:
Слагаемое \((-m\overline{w})\)носит название даламберовой инерционной силы. Обычно данное слагаемое обозначается при помощи буквы \(\overline{Ф}\).
Зная это, записываем уравнение с данным слагаемым: \(\overrightarrow{F}+\overrightarrow{R}+\overline{Ф}=0\).
Данное выражение и является математическим выражением принципа Даламбера: в случае несвободной физической точки в каждый момент времени сумма действующих сил, которые приложены к точке, инерционных сил, реакции связей, равняется нулю.
Термин «инерционная сила» в физике нередко считают формальным, его не связывают с настоящими силами. Настоящими силами могут считаться только активные силы, силы противодействия (обозначается как \(\overrightarrow{F}_{пр}\)), реакции связей. Настоящие силы в физике должны выражать значение влияния объектов в природе, могут сильно различаться по характеру воздействия.
Как сумма сил \(\overrightarrow{F}+\overrightarrow{R}\) (могут воздействовать либо на физическую точку, либо на тело) характеризуется результатом умножения \(m\overline{w}\), так и сила противодействия \(\overrightarrow{F}_{пр}\) характеризуется при помощи результата умножения \((-m\overline{w})\).
Согласно третьему закону Ньютона, действующие силы находятся в природе переменно, они являются одинаковыми по значению, однако противоположными по направлению.
Хоть сумма сил и равна нулю, это уравнение не будет считаться условием для равновесия данных сил, потому что данные силы прилагаются к различным объектам: действующая сила, а также реакция связи приложены к физической точке (телам), тогда как сила противодействия к материальным телам, которые обуславливают ускорение тела относительно инерциальной системе координат.
Метод кинетостатики можно считать формальным вариантом приведения выражений динамики к уравнениям статики, но для решения части физических задач применения данного метода является очень удобным.
Инерционная сила, которая равна произведению массы объекта на ускорение, всегда имеет направление в ту сторону, которая противоположна ускорению. Таким образом, получится такое выражение:
\(\overrightarrow{Ф}=-m\overline{w}\).
Если движение будет замедленным прямолинейным, тогда инерционная сила будет совпадать с направлением движения. В случае свободности материальной точки реакция связи будет равна нулю \(\overrightarrow{R}=0.\) Тогда уравнение станет еще проще: \(\overrightarrow{F}+\overline{Ф}=0\).
В случае проекции на координатные оси выражение будет таким: \(F_{x}-m\ddot{x}=0; F_{y}-m\ddot{y}=0; F_{z}-m\ddot{z}=0\).
Принцип невесомости
Метод Даламбера лучше всего использовать при решении задач динамики, в которых необходимо вычислить реакцию связи. Так из базового выражения принципа Даламбера следует:
\(\overrightarrow{R}=-(\overrightarrow{F}+\overrightarrow{Ф})=m\overline{w}-\overrightarrow{F}\).
С понятием реакции связи тесно связывается термин «невесомость». Данное понятие относится к состоянию, которое проявляется в случае, когда реакция базы, на которой стоит объект, равняется нулю.
Приведем пример, взяв за основу термин «перегрузка». Перегрузку обычно испытывает на себе пилот в процессе движения самолета по кругу в рамках вертикальной плоскости.
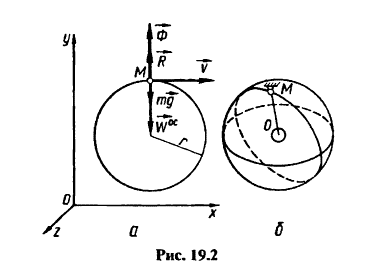
Рисунок:
Представим, что самолет совершает движение по кругу с радиусом r, а также со скоростью \(\overrightarrow{v}\). Вычислим соотношение между радиусом и скоростью такое, при котором пилот самолете будет ощущать в конкретный момент времени состояние невесомости. Если полет обладает характеристиками полета горизонтального и равномерного, тогда собственный вес пилота будет P. Пилот будет чувствовать реакцию сиденья в \(\overrightarrow{R}=-\overrightarrow{P}\).
Во период движения самолета по кругу в рамках вертикальной плоскости в произвольной точке M на пилота будет влиять сила притяжения планеты. Сила притяжения будет равна \(\overrightarrow{P}=m\overrightarrow{g}\), а также реакция сиденья будет равна \(\overrightarrow{R}\). В таком случае инерционная сила \(\overrightarrow{Ф}=-m\overline{w}\). При учете \(\mid\overline{Ф}\mid=\frac{mv^{2}}{r}\), m=P, а также при проекции активных сил на ось \(O_{y},\) получится следующее выражение: \(R-P+\frac{Pv^{2}}{gr}=0\). Из данного уравнение получаем: \(R=P(1-\frac{v^{2}}{rg})\).
Состояние невесомости наступит тогда, когда R=0. То есть наступит тогда, когда будет \(1-\frac{v^{2}}{rg}=0\) или же \(v^{2}=rg\).
Приведем пример. Если скорость \(v=900\) км\ч=250 м\с, \(g=10\frac{м}{с^{2}}\), получим: \(r=\frac{v^{2}}{g}=\frac{6,25\times10^{4}}{10}=6,25\times10^{3}=6,25 км.\)
Стоит отметить, что угловая скорость \(\omega\) вращения самолета в таком случае не будет зависеть от скорости \(v=\omega{r}\). Она будет определяться по уравнению: \(1-\frac{v^{2}}{rg}=1-\frac{\omega^{2}r^{2}}{rg}=1-\frac{\omega^{2}r}{g}=0.\) Из данного выражения получается, что \(\omega=\sqrt{\frac{g}{r}}\). Тогда период вращения будет такой: \(T=2\pi\sqrt{\frac{r}{g}}\).
Условия, которые получились в примере, вполне приемлемы для объяснения состояния невесомости космонавта на круговой орбите. В данном случае последние два выражения можно представить в виде \(r=R_{3}+h\). В данной формуле \(R_{3}\) является радиусом Земли, h высотой полета спутника. Справедливо \(h\ll{R_{3}}\), из-за этого \(r\approx{R_{3}}.\) Нужно подставить в уравнение \(R_{3}\approx6371 км\). Тогда получится: \(T=2\pi\sqrt{\frac{R_{3}}{g}}=84,4 мин\).
Принцип невозмущенности математического маятника
Период T, который был вычислен ранее, равняется периоду колебаний математического маятника, изображенного на рисунке ниже в сегменте б:
Длина математического маятника равняется земному радиусу.
Реализовать подобный математический маятник невозможно, но возможно смоделировать похожий при помощи гироскопического маятника или же неуравновешенного гироскопа. Специфика подобного математического маятника заключается в том, что он будет направлен по вертикали к центру планеты Земля, причем неважно с каким ускорением движется точка подвешивания маятника по поверхности планеты.
Выражение \(\omega=\sqrt{\frac{g}{r}}\) при \(r=R_{3}\) или \(T=2\pi\sqrt{\frac{R_{3}}{g}}=84,4\) можно считать условием для невозмутимости математического маятника.
Практическая реализация концепции невозмущенности маятника на подвижной базе предоставила возможность сформировать целый ряд невозмутимых гироскопических систем, а также сформировала целое направление в рамках технической кибернетики. Оно называется теория инвариантности (или же теория невозмутимости).
Принцип Даламбера для системы материальных точек
Представим, что в произвольной точке системы физических точек существуют действующая сила \(\overrightarrow{F_{i}}\), а также реакция связи \(\overrightarrow{R_{i}}\). Так для точки i базовое выражение динамики несвободной системы примет следующий вид: \(m_{i}\overline{w}_{i}=\overrightarrow{F}_{i}+\overrightarrow{R}_{i}, i=1,2,…,n\).
Переписываем выражение в виде: \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+(-m_{i}\overline{w}_{i})=0\) или же \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+\overline{Ф}_{i}=0, i=1,2,…,n\). В данном уравнении сила инерции \(\overline{Ф}_{i}=-m_{i}\overline{w}_{i}\). Согласно индексу i получится, что \(\sum_{i=1}^{n}\overrightarrow{F}_{i}+\sum_{i=1}^{n}\overrightarrow{R}_{i}+\sum_{i=1}^{n}\overrightarrow{Ф}_{i}=0\).
Установив основные векторы действующих сил, реакции связи, а также инерционных сил через \(\overrightarrow{F}=\sum_{i=1}^{n}\overrightarrow{F}_{i} \overrightarrow{R}=\sum_{i=1}^{n}\overrightarrow{R}_{i}\)
\(\overrightarrow{Ф}=\sum_{i=1}^{n}\overrightarrow{Ф}_{i}\) получится выражение: \(\overrightarrow{F}+\overrightarrow{R}+\overrightarrow{Ф}=0\).
Выберем произвольный центр O. Далее необходимо провести в i точку системы радиус-вектор \(\overrightarrow{r_{i}}\), умножить векторно на силы, входящие в \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+\overline{Ф}_{i}=0\). Далее нужно определить моменты сил по отношению к центру O. Далее, прибавляя по i, нужно определить базовые моменты действующих сил реакции связей и инерционных сил:\( \overline{M^{акт}_{O}}+\overline{M^{p}_{O}}+\overline{M^{in}_{O}}=0\)
Посмотрите на рисунок:
Здесь
Выражения \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+\overline{Ф}_{i}=0\) и \(\overline{M^{акт}_{O}}+\overline{M^{p}_{O}}+\overline{M^{in}_{O}}=0\) показывают принцип Даламбера для системы.
В каждый период времени векторная сумма основных векторов действующих или заданных сил, инерционных сил, реакций связи подвижной системы физических точек равняется нулю. Также векторная сумма основных моментов действующих сил, реакций связи и инерционных сил подвижной системы равняется нулю.
Выражениям \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+\overline{Ф}_{i}=0\) и \(\overline{M^{акт}_{O}}+\overline{M^{p}_{O}}+\overline{M^{in}_{O}}=0\) в вектором варианте могут соответствовать шесть уравнений в координатном виде:
Делать проекцию данных выражений возможно и на неподвижные, и на подвижные координатные оси. Выражения, показанные на рисунке выше, носят название уравнений кинетостатики. Для того, чтобы пользоваться ими, необходимо уметь рассчитывать инерционные силы системы материальных точек, а также твердого тела.
Расчет инерционных сил материальной точки
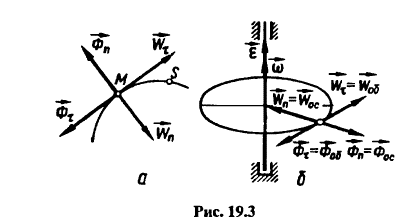
Если движение материальной точки задается натуральным способом, тогда ускорение точки будет равняться векторной сумме касательного (или же тангенциального) и нормального ускорений. Из-за этого необходимо ввести касательную (или тангенциальную) \(\overrightarrow{Ф}_{\tau}\) и нормальную \(\overrightarrow{Ф}_{n}\) инерциальной силы.
Данные силы будут вычисляться по таким формулам:
\(\overrightarrow{Ф}_{\tau}=mw_{\tau}=m\frac{dv_{\tau}}{dt}=m\frac{d^{2}s}{dt^{2}}\)
\(\overrightarrow{Ф}_{n}=mw_{n}=m\frac{v^{2}}{\rho}\).
В случае, если физическая точка является одной из точек твердого объекта, который вращается вокруг неподвижной оси с угловой скоростью в \(\overline{\omega}\) и с угловым ускорением \(\overline{e}\), тогда ускорение оси совпадет с нормальным, вращательное ускорение совпадет с тангенциальным.
Выделяем данным видам ускорения инерционные силы, исходя из выражений ниже: \(Ф_{об}=Ф_{\tau}=mw_{\tau}, w_{\tau}=w_{об}=er; Ф_{ос}=Ф_{n}=mw_{n}, w_{n}=w_{оc}=\omega^{2}r.\)
Инерционные силы имеют направление в противоположную для ускорения сторону.
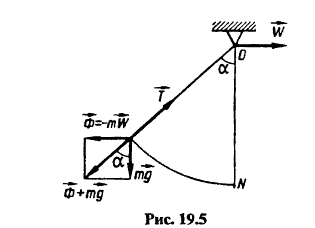
Груз M, у которого вес P=1H, который подвесили на нитке с длиной в AM=3 м. Данный груз вращается вокруг оси \(O_{z}\). В положении горизонтальной плоскости точка M описывает круг. Нитка с вертикалью формирует неизменный угол \(a=\frac{\pi}{3}\). Нужно найти натяжение \(\overrightarrow{r}\) нити, а также скорость v груза.
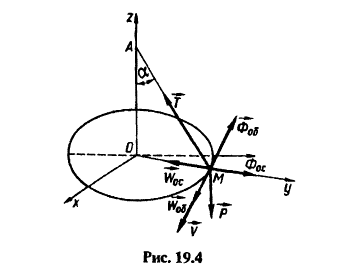
Рисунок конструкции:
Решение.
Начинать решение всех динамических задач нужно с проведения анализа действующих сил, а также построения схемы всех действующих сил. Согласно условию задачи необходимо определить реакцию нити, из-за этого использовать возможно принцип Даламбера. В случае данной задачи на груз воздействует сила тяжести \(\overrightarrow{P}\). Груз M вступает во взаимодействие с нитью, из-за чего происходит реакция \(\overrightarrow{T}\), которая направляется к точке закрепления нити по самой нити. Можно пренебречь силой сопротивления воздуха из-за малой скорости \(\overrightarrow{v}\) движения.
Теперь найдем инерционные силы. Для этого нужно понять, что составляет вектор ускорения. Из-за того, что точка M совершает действие по кругу, тогда ускорение данной точки возможно разложить на вращательное ускорение \(\overrightarrow{w}\), а также осевое \(\overrightarrow{w_{ос}}\).
Необходимо построить векторы осевого и вращательного ускорений, найдя из величины по формулам: \(Ф_{об}=Ф_{\tau}=mw_{\tau}\), \(w_{\tau}=w_{об}=er\); \(Ф_{ос}=Ф_{n}=mw_{n}\), \(w_{n}=w_{оc}=\omega^{2}r\).
На рисунке выше показано, как нужно проектировать действующие силы на оси системы координат. При учете v=const получится, что \(Ф_{ос}-T\sin\alpha\), \(T\cos\alpha-P=0\). Из второго выражения получается \(T=\frac{P}{\cos\alpha}=2H\), выделяем из второго выражения v. Так как
Тогда
\(v^{2}=\frac{\tan{AM}\sin^{2}\alpha}{P}=2\times9,8\times3\times\frac{3}{4}\approx44,1\Rightarrow{v}\approx6,64\).
Необходимо рассчитать угол \(\alpha\), на который сделал наклон маятник от вертикали ON в процессе движения горизонтальной базы при ускорении \(\overrightarrow{w}\). Вертикаль находится в горизонтальной плоскости.
Решение
Нужно заменить влияние нити на маятник с помощью реакции \(\overrightarrow{T}\). Из условий задачи известны: вес маятника \(m\overrightarrow{g}\), реакция нити \(\overrightarrow{T}\), а также инерционная сила \(\overrightarrow{Ф}=-m\overrightarrow{w}\).
Посмотрите на рисунок:
В положении отклонения маятника на угол \(\alpha\) сумма моментов действующих сил относительно точки O, на которую подвешивают нить, должна равняться нулю. Из-за того, что реакция нити \(\overrightarrow{T}\) постоянно проходит через центр O, выходит, что вектор \(\overline{Ф}+m\overrightarrow{g}\) должен направляться по нитке (при другом раскладе момент сил не равняется нулю). Из рисунка следует, что \(\tan\alpha=\frac{w}{g}\).
Получается, что угол \(\alpha\) не обладает никакой зависимостью от веса маятника, а также от длины маятника. Таким образом, все маятники совершают отклонение на равные углы от вертикали в случае движения точек их подвешивания с равным ускорением.
Расчет основного вектора, а также основного момента сил инерции для твердого объекта
По формулам \(\overrightarrow{F}_{i}+\overrightarrow{R}_{i}+\overline{Ф}_{i}=0\) и \(\overline{M^{акт}_{O}}+\overline{M^{p}_{O}}+\overline{M^{in}_{O}}=0\) основной вектор, а также основной момент действующих сил инерции после некоторых преобразований можно записать так:
В данной формуле A является центром моментов. Возможно записать выражение в следующем виде, если вспомнить значение количества движений и кинетического момента системы:
Становится понятно, что для расчета основного вектора и основного момента инерционных сил твердого тела возможно пользоваться теоремами об изменении количества движения, а также основного момента количества движения объекта, а, значит, использовать любой вид записи в разных системах координат в зависимости от задачи, которая поставлена.
Основной вектор инерционных сил твердого тела равняется инерционной силе центра масс, если сделать предположение, что в этом центре находится вся масса данного тела.
Основной момент инерционных сил, по базовым формулам, в зависимости от того, какая выбрана система координат, примет такой вид:
Если полюс O переместить в центр масс C объекта, тогда два последних уравнения возможно записать проще:
Все формулы, которые были приведены, сильно упрощаются в случаях, когда исследуется движение твердого тела.
Инерционная сила Даламбера
Сила инерции — векторное значение, которое равно произведению ускорения и массы точки, которая направлена в противоположную сторону от ускорения.
Сила Даламбера является несуществующей в реальной жизни величиной. Ее нереально измерить, ее используют в инерциональных системах отсчета для того, чтобы применить искусственный метод — упростить выражение динамики до выражения статики.
Где используют принцип Даламбера
Принцип кинетостатики позволяет записывать движение произвольной системы в форме выражений, а также решать задачи динамики при помощи методов статики. Из-за этого принцип Даламбера используется инженерами крайне широко. Также принцип Даламбера используется для того, чтобы найти неизвестные части выражения.
Пример решения задачи с использованием принципа Даламбера
Порядок решения задач с использованием принципа Даламбера
Желательно решать задачи с использованием принципа Даламбера (как метода кинетостатики) с использованием следующего плана:
- Показать на чертеже все действующие силы, которые прилагаются к каждой физической точке.
- Показать реакции связей на рисунке.
- К действующим силам на рисунке добавить реакции связей инерционных сил материальных точек системы.
- Избрать систему координат для расчетов.
- Составить уравнение статики для всех действующих сил.
- Решить получившуюся систему уравнений, определить искомые значения.
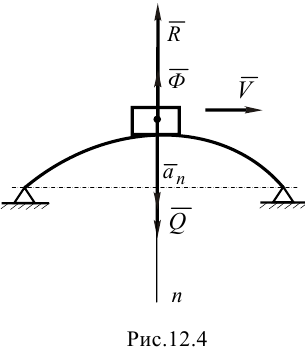
Автомобиль с весом Q=10 кН совершает движение по мосту выпуклой формы, развивая скорость V=10 м/с, радиус кривизны моста составляет \(\rho=50\) м. Нужно найти давление автомобиля на мост в тот момент, когда автомобиль пересекает середину данного моста.
Решение. На автомобиль будут воздействовать сила тяжести \(\overrightarrow{Q}\), реакция моста \(\overrightarrow{R}\), которая будет равняться по значению давлению \(\overrightarrow{N}\) автомобиля на мост. Данные силы никак не компенсируют друг друга из-за того, что автомобиль совершает движение по криволинейной траектории с обычным ускорением, которое имеет направление к центру кривизны. Если к силам \(\overrightarrow{Q}\) и \(\overrightarrow{R}\) добавить силу инерции \(\overrightarrow{Ф}\), направление которой — в сторону, которая противоположна нормальному ускорению \(\overrightarrow{a_{n}}\), и которая будет равна по значению:
Тогда система сил \(\overrightarrow{Q}\), \(\overrightarrow{R}\) и \(\overrightarrow{Ф}\) будет находиться в статике, а, значит:
Так как все активные силы влияют по одной прямой, совпадающей с нормалью n, спроецируем силы на нормаль n:
Давление N автомобиля на мост будет равно значению \(\overrightarrow{R}\):
Ответ: 7,96 кН.
Груз M с весом 1H весит на нитке длиной 30 см. Весит в неподвижной точке O, то есть является коническим маятником, который описывает окружность в горизонтальной плоскости. При всем этом нить образует с вертикалью угол \(\alpha=60^{\circ}\). Нужно найти скорость груза, а также натяжение нити.
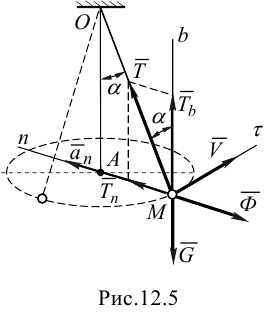
Взгляните на рисунок:
Решение. На груз M воздействует сила тяжести \(\overrightarrow{G}\) и реакция нити \(\overrightarrow{T}\). Данные силы не компенсируются из-за движения груза. Движение совершается по криволинейной траектории окружности с радиусом AM, а также обычным ускорением.
Рассчитаем силу инерции объекта. Сила инерции направляется по радиусу в сторону, которая противоположна ускорению, но равна по модулю:
Теперь нужно связать с точкой M систему координат. Ось \(M_{\tau}\)нужно направить по касательной в направлении вектора скорости \(\overrightarrow{V}\), ось \(M_{n}\) по нормали, а ось \(M_{b}\) перпендикулярно плоскости, в которой лежат остальные две оси.
Применяем принцип Даламбера, сумма сил равна нулю.
Натяжение нити T:
Ответ: T=2 H, V=2,1 м\с.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так