Формулировка принципа суперпозиции электрических полей

Что такое принцип суперпозиции в физике

Принцип применяется в отношении систем или же электрических полей, что можно описать посредством линейных уравнений. Имеет большую значимость в большом количестве отделов традиционной физики: механике, волновой и колебательной теориях, теориях физических полей и т.д. 

Специфицировать формулировку можно в отношении некоторого круга конкретных физических областей. К примеру, в рамках механики в традиционной дефиниции принцип суперпозиции трактуется, как: 

• итог влияния на частицу некоторого количества сил извне является векторным результатом сложения эффектов данных сил; 
• всякое осложненное действие возможно поделить на два или больше более легких. 

Более часто встречается принцип суперпозиции в электростатической физике. Так, напряженность электростатического поля, которое создается в определенной точке комплексом зарядов, является результатом сложения векторов напряженности полей конкретных зарядов. Принцип суперпозиции способен вбирать и другие дефиниции. Среди них, например: 

• энергия взаимовлияния абсолютно всех частиц в рамках системы с большим количеством частиц является всего лишь результатом сложения энергии парных взаимовлияний между всеми вероятно существующими парами частиц — в комплексе не наблюдается многочастичных взаимовлияний; 
• уравнения, которые описывают характер многочастичного комплекса, считаются линейными по числу частиц. 

Можно говорить о том, что линейность традиционной физической теории в конкретной сфере физики является первопричиной появления в данной области принципа суперпозиции. 

Принцип суперпозиции рассматривают в качестве следствия, которое сразу же получается из исследуемой физической теории. Приведем простой пример: в электростатике данный принцип является следствием такого явления, как линейности уравнения Максвелла в условиях вакуума. Из данного факта получается, что возможная энергия электростатического взаимного действия комплекса заряженных точек может быть посчитана посредством вычислений потенциальной энергии всех пар заряженных точек. 

Иным следствием факта того, что уравнение Максвелла является линейным, считается факт, что световые лучи не рассеиваются и никаким образом не влияют друг на друга. Можно говорить о том, что данный закон — формальный принцип суперпозиции в оптической физике. 

Получается, что принцип суперпозиции в электродинамике является не нерушимым законом всего живого, а только следствием того, что уравнение Максвелла является линейным, то есть следствием уравнений традиционной электродинамики. Из-за этого, когда происходит выход за рамки используемости традиционной электродинамики можно ждать того, что принцип суперпозиции будет нарушен.

Характерные черты принципа суперпозиции электрических полей

Представим, что перед нами три точки, которые имеют электрический заряд. Между всеми этими точками существует взаимодействие. В данном случае возможно поэкспериментировать и рассчитать количество сил, что влияют на отдельные заряды. Для нахождения общей силы, с которой происходит воздействие одного заряда на другой, нужно силы, которые влияют на каждый заряд, прибавить друг к другу в соответствии с правилом параллелограмма. В данном случае появляется крайне важный вопрос, будет ли равняться измеряемая сила, что воздействует на все заряды, результату сложения сил других двух зарядов при условии, что силы высчитываются по закону Кулона. Измерения показывают, что расчетная сила будет равняться результату сложения расчетных сил по закону Кулона в отношении остальных точечных зарядов. Данный итог можно выразить в качестве таких принципов, как:

• сила взаимного влияния двух заряженных точек не меняется при условии, что существуют иные заряды; 
• сила, которая воздействует на заряженную точку со стороны иных заряженных точек, равняется результату сложения сил, которые действуют на данный заряд со стороны всех заряженных точек в случае неимения иного. 

Именно в этих двух принципах заключается суть принципа суперпозиции электрических полей. Можно говорить о том, что данный принцип — часть базовой теории о работе электричества. Его значимость для данной сферы такая же, как у закона Кулона. Обобщить данный принцип возможно даже в случае большого количества зарядов. В случае, если есть некоторое количество источников поля (числа заряженных точек N), то итоговую силу, которая воздействует на экспериментальный заряд q, возможно рассчитать таким образом: \(\overrightarrow{F}=\sum_(i=1)^N\overrightarrow{F}_{ia}\). 

В данной формуле \(\overrightarrow{F}_{ia}\) является силой, что воздействует на заряженную точку q заряженная точка \(q_{i}\) в случае, если иные N-1 заряженные точки не существуют. 

Полевая дефиниция принципа суперпозиции

У принципа суперпозиции есть полевая дефиниция: напряженность поля двух заряженных точек равняется результату сложения напряженностей, что формируются каждой отдельной заряженной точкой при условии, если другого не существует. В данном случае принцип суперпозиции в отношении напряженностей записывается таким образом: \(\overrightarrow{E}=\sum\overrightarrow{E}_{i}. \) 

В этой формуле \(\overrightarrow{E}_{i}=\frac{1}{4\pi\epsilon_{0}}\frac{q_{i}}{\epsilon{r_i^3}}\overrightarrow{r}_{i}\)  равна напряженности i-заряженной точки, \(\overrightarrow{r}_{i}\) — векторный радиус, который проводится от i-заряженной точки в пространственную точку. 

Формула \(\overrightarrow{F}=\sum_(i=1)^N\overrightarrow{F}_{ia}\) показывает, что напряженность полей произвольных чисел заряженных точек равняется результату сложения напряженностей полей отдельных заряженных точек при условии отсутствия иных. Экспериментально было доказано, что данный принцип может быть соблюден даже в случае крайне больших значений напряженности поля. Самые большие напряженности обладают полями в своих ядрах или даже атомах (это \(10^{11}-10^{17}\frac{B}{M}\)). В отношении данных напряженностей применяли принцип суперпозиции в вычислении энергетических атомных уровней. Результаты вычислений были одинаковыми с тем, что получилось в ходе первичных исследований, причем точность расчетов была крайне высокой. 

В случае, если заряженная точка распределяется беспрерывно (в таком случае не нужно брать в расчет дискретность), тогда общие показатели напряженности электрического поля будут рассчитываться по такой формуле: \(\overrightarrow{E}=\int d\overrightarrow{E}\). В данной формуле интегрирование происходит по области распространения заряженных точек. В случае, если заряженные точки распределяются по линии (формула линейной плотности распределения заряда: \(\tau=\frac{dq}{dl}\)), интегрирование в \(\overrightarrow{E}=\int d\overrightarrow{E}\) совершают линейно. В случае, когда заряды распределяются по поверхностям, а плотность данной поверхности \(\sigma=\frac{dq}{dS}\), интеграция происходит по поверхности. 

Объемное интегрирование совершают в случаях, когда распределение заряженных точек происходит по объему: \(\rho=\frac{dq}{dV}\). В этой формуле \(\rho\) является плотностью объема распределения заряженной точки. 

Посредством принципа суперпозиции возможно определить \(\overrightarrow{E}\) для всех точек в пространстве по понятному распределению в пространстве заряженной точки. 

Примеры задач с суперпозицией электрических полей

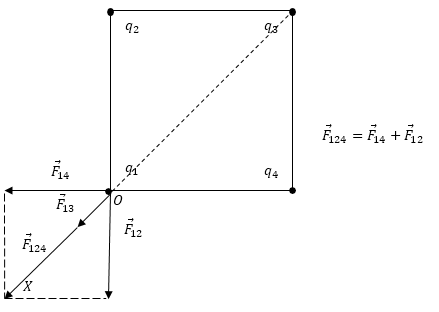
Решение данной задачи: сначала нужно показать на рисунке все силы, которые воздействуют на один из зарядов в верхней части квадрата (выбрать можно абсолютно любой, потому что заряды абсолютно одинаковые). 

Рисунок будет выглядеть таким образом: 

Источник: calc.ru

Итоговую силу, которая воздействует на заряд \(q_{1}\) , можно записать таким образом: \(\overrightarrow{F}=\overrightarrow{F}_{12}+\overrightarrow{F}_{14}+\overrightarrow{F}_{13}\). Сила \(\overrightarrow{F}_{12} и \overrightarrow{F}_{14}\) являются равными по собственному модулю, поэтому их можно найти таким образом: \(\mid\overrightarrow{F}_{12}\mid=\mid\overrightarrow{F}_{14}\mid=k\frac{q^{2}}{a^{2}}\). В данной формуле \(k=9\times10^{9}\frac{Нм^{2}}{Кл^{2}}\). 

Модуль у силы \(\overrightarrow{F}_{13}\) возможно рассчитать по закону Кулона, при этом нужно понимать, что квадратная диагональ равняется \(d=\sqrt{2a}\). Получается, что \(\mid\overrightarrow{F}_{13}\mid=k\frac{q^{2}}{2a^{2}}\). Если направить ось OX таким же образом, как и на рисунке, то можно получить вот это уравнение:\( \overrightarrow{F}=\overrightarrow{F}_{12}+\overrightarrow{F}_{14}+\overrightarrow{F}_{13}\) . Нужно подставить в выражение все данные по модулям сил и рассчитать: \(F=2k\frac{q^{2}}{a^{2}}\times\frac{\sqrt{2}}{2}+k\frac{q^{2}}{2a^{2}}=\frac{kq^{2}}{2a^{2}}=\frac{kq^{2}}{a^{2}}(\frac{2\sqrt{2}+1}{2})\).

Ответ: сила, воздействующая на отдельные заряженные точки в верхней части квадрата равняется \(F=\frac{kq^{2}}{a^{2}}(\frac{2\sqrt{2}+1}{2})\). 

Посмотрите на рисунок для данной задачи: 

Источник: calc.ru

Решение будет таким: выделяется на нити заряженная точка dq. Для данной точки необходимо выписать уравнение из закона Кулона для нахождения напряженности электрического поля. Формула выглядит так: \(d\overrightarrow{E}=k\frac{dq}{r^{3}}\overrightarrow{r}\). 

В той точке, которая дана в задаче, все векторы напряженности имеют одинаковую ориентацию по оси X, из-за этого получается: \(dE_{x}=k\frac{dq}{r^{2}}=dE\). Из-за того, что заряд, согласно условиям задания, распределяется по нити равномерно с плотностью линии \(\tau\), получается, что можно сделать такую запись: \(dq=\tau{d}r\). Теперь возможно в уравнение \(d\overrightarrow{E}=k\frac{dq}{r^{3}}\overrightarrow{r} подставить dq=\tau{d}r\). Происходит следующая интеграция: \(E=k\int_{a}^{l+a} \frac{\tau{dr}}{r^{2}}=kr(-\frac{1}{r}\mid_a^{l+a})=\frac{k\tau{l}}{a(l+a)}\) .

Ответ: напряженность электрического поля нити в заданной точке можно рассчитать по формуле \(E=\frac{k\tau{l}}{a(l+a)}\).