Производственная функция Кобба-Дугласа

Функция Кобба-Дугласа — это

Функция Кобба-Дугласа названа в честь американских экономистов Чарльза Кобба и Пола Дугласа. Они представили эту производственную функцию в 1928 году в статье, опубликованной в журнале American Economic Review. Статья называлась «Теория производства» и была основана на их эмпирическом исследовании взаимосвязи между затратами (труда и капитала) и выпуском продукции в обрабатывающей промышленности. Одна из наиболее широко используемых производственных функций для изучения поведения производства.

В качестве входов выступают различные факторы производства — земля, труд, капитал и предприятия, а в качестве выходов — товары и услуги. Производственная функция может предоставить нам максимум товаров и услуг, которые мы можем произвести при заданном количестве вводимых ресурсов. Кроме того, она может помочь определить, какие ресурсы необходимы для достижения минимального уровня производства.

Формула

Математическая форма производственной функции Кобба-Дугласа для одного выпуска с двумя факторами может быть записана как:

???? = ????(????, ????, ????) = ????????????????1-????

Где:

Y: количество продукции;

L: количество труда, затраченного на производство Q, например, часы труда в месяц;

K: часы работы капитала, использованные для производства Q, например, часы работы станка для производства Q;

A: Уровень технологии или общая производительность факторов производства (A>0);

α: Постоянная между 0 и 1 (0< α <1).

Краткосрочный и долгосрочный периоды

Рассматривать производственную функцию можно через два временных интервала — краткосрочный и долгосрочный. Краткосрочный — это промежуток времени, в течение которого мы можем изменять только переменные факторы производства.

В данном случае речь идет о тех переменных факторах, которые мы можем изменить за небольшой промежуток времени, например, количество рабочей силы, сырья, топлива, электроэнергии и т. д. Символически Q= T(K, L). Далее это делается с помощью закона переменных пропорций.

Очевидно, что в долгосрочном периоде мы можем менять все факторы производства, то есть как постоянные, так и переменные факторы. Можно изменить размер фабрики, методы производства, машины, количество рабочих, энергию, топливо и так далее.

Таким образом, производственная функция принимает различные формы в зависимости от двух временных рамок. Очевидно, что мы изучаем производственную функцию относительно двух различных временных рамок. Долгосрочная производственная функция является предметом закона отдачи от масштаба.

Основные характеристики

Отдача от масштаба

Три вида:

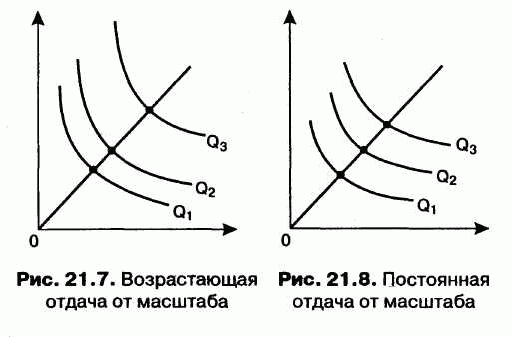
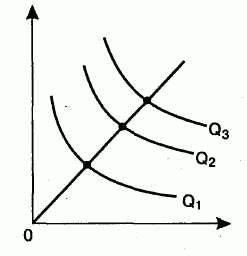
1. Возрастающая отдача от масштаба: увеличение отдачи от масштаба происходит, когда объем выпуска увеличивается в большей пропорции, чем увеличение вводимых ресурсов. Если все факторы увеличиваются на 20%, то выпуск увеличивается, скажем, на 30%. Таким образом, при удвоении факторов выпуск увеличивается более чем в два раза.
2. Постоянная отдача от масштаба: возникает, когда объем производства увеличивается в той же пропорции, что и объем вводимых ресурсов. Если все факторы увеличиваются на 20%, то и выпуск увеличивается на 20%. Таким образом, удвоение всех факторов приводит к удвоению объема выпуска, поэтому отдача от масштаба постоянна. Постоянная отдача от масштаба также называется линейно однородной производственной функцией.

3. Уменьшающаяся отдача от масштаба: происходит, когда объем выпуска увеличивается в меньшей пропорции, чем рост вводимых ресурсов. Если все факторы увеличиваются на 20 %, то выпуск увеличивается менее чем на 20 %.

   Функция Кобба-Дугласа демонстрирует постоянную отдачу от масштаба. Постоянная отдача от масштаба имеет место, когда выпуск увеличивается в той же пропорции, что и увеличение вводимых ресурсов. При постоянной отдаче от масштаба сумма двух экспонент для капитала и труда равна единице, т. е. α + (1-α) =1.

Источник: inventech.ru

Постоянный возврат к масштабу происходит, когда объем производства увеличивается в той же пропорции, что и объем вводимых ресурсов.

Предельный продукт

∂Q/∂L

В случае функции Кобба-Дугласа:

∂Q/∂L = Aβ L(β-1) Kα

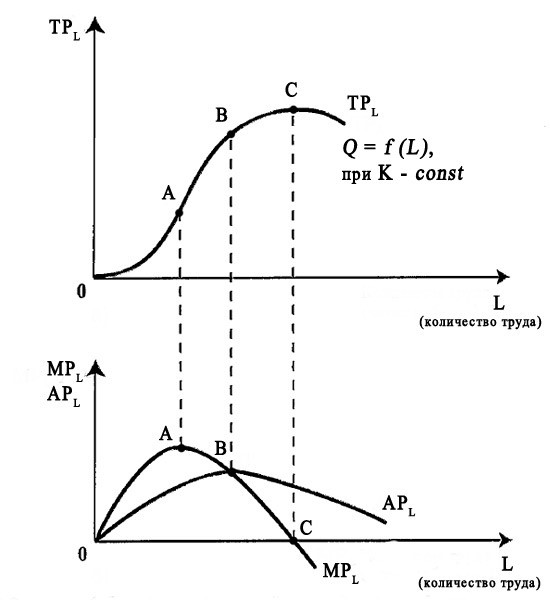
При увеличении L или K общий объем выпуска увеличивается, то есть предельный продукт положителен.

Как видно из следующих графиков, предельный продукт уменьшается.

 

Источник: economicportal.ru

Производственная функция Кобба-Дугласа линейна в логарифме.

???? = ????(????, ????, ????) = ????????????????1-????

Применив логарифм к обеим сторонам, получим

ln ???? = ln ???? + ???? ln ???? + (1-????) ???????? ????

Где:

α — частичная эластичность выпуска по отношению к капиталу. Она измеряет процентное изменение объема выпуска, скажем, при одном процентном изменении вводимого капитала при неизменных затратах труда.

(1-α) — частичная эластичность выпуска по труду. Она измеряет процентное изменение объема выпуска, скажем, на одно процентное изменение затрат труда при неизменных затратах капитала.

Функция Кобба-Дугласа линейна по параметру. Ее можно оценить с помощью метода наименьших квадратов.

Эластичность выпуска

(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)

Если эластичность выпуска больше 1, то производственная функция эластична, и наоборот. В случае производственной функции Кобба-Дугласа эластичность выпуска можно измерить довольно просто:

(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)

= [ Aβ L(β-1) Kα ] / [ A Lβ Kα / L ]

= [ Aβ L(β-1) Kα ] / [ A L(β-1) Kα ] = β

Эластичность выпуска по отношению к труду постоянна и равна β. Если β равен 0,2, а труд увеличился на 10%, то выпуск увеличится на 2%.

α и β — эластичность выпуска по капиталу и труду, они постоянны.

График

Источник: seinst.ru

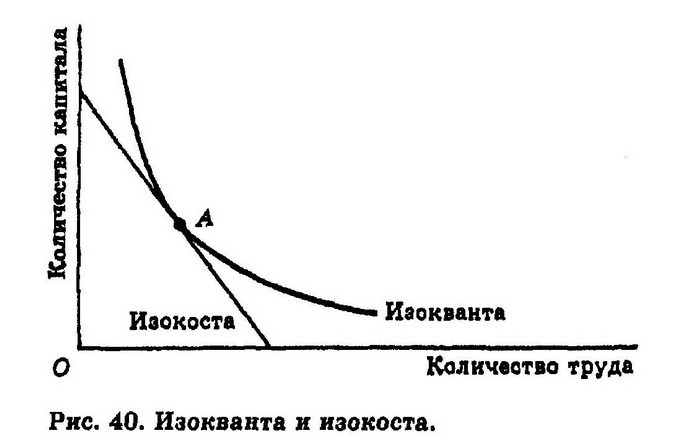
1. Изокванта показывает все комбинации факторов, которые производят определенный объем продукции
2. Изокоста показывает все комбинации факторов, которые обходятся в одну и ту же сумму.
3. Изокосты и изокванты могут показать оптимальное сочетание факторов производства для получения максимального объема выпуска при минимальных затратах.

Кобб и Дуглас сами признавали, что их производственная функция не опирается на прочный теоретический фундамент, и ее не следует понимать как закон производства. Она лишь представляет собой статистическое приближение к наблюдаемым взаимосвязям между производственными затратами и выпуском. Тем не менее ее простые математические свойства привлекательны для экономистов и привели к тому, что она стала стандартной моделью, используемой в экономической теории на протяжении последнего столетия.