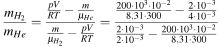Что нужно знать о законах Дальтона — основные сведения
Что такое законы Дальтона
Долгие годы исследований в сфере газов, которые проводил английский физик и химик Джон Дальтон, завершились созданием закона, названного в честь самого ученого.
Данный закон гласит, что парциальное давление конкретных газов в составе смеси являются независимыми. Что такое смесь газов?
Смесь газов — совокупность нескольких различных газов, которые не вступают ни в какую химическую реакцию в заданных условиях.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Законы Дальтона — вид физических законов, по условию которых происходит подчинение свойств газовых смесей.
История открытия законов Дальтона
Английский химик и физик Джон Дальтон проводил эксперименты по изучению поведения газов в атмосфере. В то время было интересно, как происходят различные природные явления, им была изучена метеорология.
Джон Дальтон задумался над вопросом, почему газы не находятся в сосуде в качестве отдельных слоев, а не смешиваются, однако при этом не часто взаимодействуют друг с другом. Данные наблюдения способствовали открытию нового закона в рамках физики о парциальном давлении газов.
Первый закон Дальтона называется законом парциальных давлений смесей газов, которые определяют суммарное давление. Данный закон был открыт в 1801 году, а описан позднее — в 1802 году. Второй закон Дальтона описывает относительную растворимость смеси газов в жидкости. Часто второй закон Дальтона именуется законом Генри-Дальтона.
Также Джон Дальтон сформулировал закон кратных отношений в 1803 году. Данный закон в химии обуславливает следующее: если два элемента образуют друг с другом более одного типа соединения, то массы одного из элементов, которые приходятся на одну и ту же массу иного элемента, относятся как целые небольшие числа.
Джон Дальтон (годы жизни — 1766-1844) является английским физиком и химиком. Родился в графстве Камбрия, в городе Иглсфилде, в семье квакеров. Джон Дальтон покинул школу в возрасте 11 лет, после чего начал увлекаться метеорологией. Позже он стал работать сельскохозяйственным рабочим, устроился ассистентом в квакерскую школу. Все свои сведения в сфере математики и естественных наук Джон Дальтон получил от собственных коллег по школе. Позже открыл ради обогащения собственную школу. Главный вклад Джона Дальтона в современную нам науку — атомная теория. Интерес мальчика к погодным изменениям, а также поведению газов в смеси привел Дальтона к мысли об атомах.
Так выглядел Джон Дальтон:
Формулировка и формулы законов Дальтона
Рассмотрим основные формулировки законов Дальтона.
Закон о суммарном давлении смеси газов
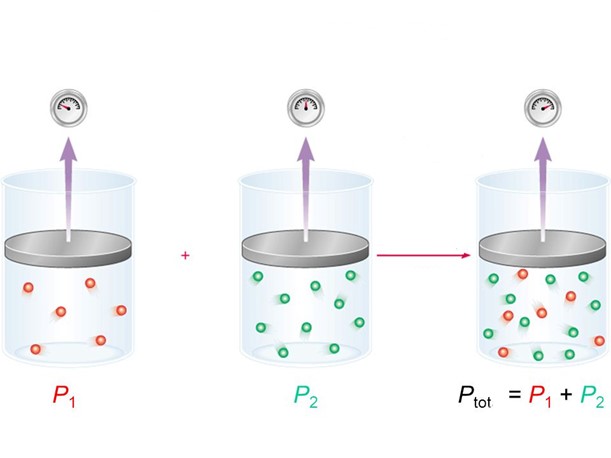
Первый закон Дальтона. Давление смеси идеальных газов, которые не взаимодействуют между собой, равняется сумме парциальных давлений этих газов. Исходя из этого можно сказать, что парциальное давление элемента газовой смеси равняется произведению давления смеси на молярную долю данного элемента.
\(P=\sum_{i=1}^np_{i}=p_{1}+p_{2}+...+p_{n}\)
Закон о парциальном давлении в газовой смеси
В 1801 году Джоном Дальтоном был выведен закон, который гласил, что давление смеси некоторого количества газов будет равняться сумме парциальных давлений всех газов, которые составляют смесь. Данный закон носит название закона о парциальном давлении в газовой смеси.
Парциальное давление каждого газа, который входит в состав смеси, является давлением, которое создавалось бы такой же массой этого газа, если он будет занимать весь объем смеси при такой же температуре.
Закон Джона Дальтона объясняет, что давление смеси идеальных газов является суммой парциальных давлений элементов смеси.
Парциальное давление — такой вид давления, величину которого компонента оказала бы при условии, что она бы заняла все место, которое было занято смесью газов.
Данный закон показывает, что на каждый элемент смеси газов не происходит воздействие присутствия других элементов, а свойства каждого элемента в составе смеси не изменяются.
Закон о растворимости газов
Его также называют законом о растворимости компонентов газовой смеси. Данный закон часто носит название закона Генри. Закон Генри был описан британским химиком Уильямом Генри в 1803 году. Закон Генри гласил: при постоянной величине температуры растворимость в конкретной жидкости каждого из элементов смеси газов, которая находится над жидкостью, носит пропорциональный характер к парциальному давлению этих газов.
Закон Дальтона о растворимости газов звучит следующим образом:
Растворимость элемента смеси газов в конкретной жидкости при постоянной температуре будет пропорциональной парциальному давлению данного элемента. Растворимость не зависит от происхождения иных элементов в смеси и давления газовой смеси.
\( m_{i}=\frac{p_{i}}{P}\)
Пределы применимости законов
Законы Дальтона справедливы только для идеальных газов. Для реальных газов возможно применять данные законы только при условии, что растворимость этих газов крайне невелика, характер этих газов практически совпадает с характером идеального газа.
Идеальный газ — теоретическая модель, которая описывает поведение реальных газов. Молекулы в статике не соприкасаются у таких газов. Они начинают взаимодействовать только в случае столкновения друг с другом или стенками сосуда, в котором находятся.
Закон о суммарном давлении газовой смеси очень точно соблюдается при крайне низких показателях давления. Тогда наблюдается среднее расстояние между молекулами газа большего размера, чем они сами. Так взаимодействие молекул сводится практически к нулю. При обычных малых давлениях закон о суммарном давлении соблюдается приближенно. В случае высокого давления можно говорить о большом отклонении от данного закона.
Следствие закона Дальтона
Следствием из закона Дальтона будет такое утверждение: количество молекул каждого элемента смеси будет воздействовать на стенки сосуда, причем неважно, какое количество элементов находится в газовой смеси. Значит, общее давление всех газов в газовой смеси будет воздействием всех молекул, которые содержатся в сосуде.
Закон Дальтона не будет работать, если на газовую смесь оказывается воздействие при помощи высокой температуры или же высокого давления. При таких обстоятельствах газы в сосуде могут начать вступать во взаимодействие друг с другом.
Уравнение закона Дальтона
Уже много раз отмечалось, что конкретные элементы газовой смеси можно считать автономными и независимыми. Из-за этого каждый элемент создает давление, которое вычисляется так:
\(p=p_{i}kT.\)
Полноценное давление смеси газов можно рассчитать таким образом:
\(p=p_{1}kT+p_{2}kT+...+p_{i}kT=p_{1}+p_{2}+...+p_{n}\).
В данных формулах \(p_{i}\) является показателем парциального давления i газового элемента. Данное уравнение является законом Дальтона.
В большей концентрации веществ, а также при больших давлениях закон Дальтона применить в точности не получится. Потому что, как говорилось ранее, появится взаимодействие между элементами газовой смеси. Элементы перестают обладать независимостью. Джон Дальтон объяснил собственный закон через атомистическую гипотезу.
Доказательство закона:
Пусть существует i элемент газовой смеси. Таким образом уравнение Менделеева-Клайперона примет следующий вид:
\((p_{1}+p_{2}+...+p_{i})V=(\frac{m_{1}}{\mu_{1}}+\frac{m_{2}}{\mu_{2}}+...+\frac{m_{i}}{\mu_{i}})RT\)
В данной формуле \(m_{i}\) является массой элемента газовой смеси, а \(\mu_{i}\) является молярной массой элемента газовой смеси.
Если применить \(\langle\mu\rangle\) такого типа, что:
\(\frac{1}{\langle\mu\rangle}=\frac{1}{m}[\frac{m_{1}}{\mu_{1}}+\frac{m_{2}}{\mu_{2}}+...+\frac{m_{i}}{\mu_{i}}]\).
Тогда можно записать уравнение в форме: \(pV=\frac{m}{\langle\mu\rangle}RT\).
Закон Дальтона возможно записать в форме:
\(p=\sum_{i=1}^Np_{i}=\frac{RT}{V}\sum_{i=1}^NV_{i}\)
Следствие закона Дальтона будет таким:
\(p{i}=x_{i}p\)
В данном выражении \(x_{i}\) является молярной концентрацией i элемента газа в смеси. Также нужно помнить об этом:
\(x_{i}=\frac{v_{i}}{\sum_{i=1}^NH_{i}}\)
Где \(v_{i}\) является количеством молей i элемента газа в смеси.
Особые условия закона Дальтона
Чтобы лучше понять закон Дальтона для газовой смеси нужно понять, что такое идеальный газ.
Для идеального газа будут справедливы такие требования как:
- размер атомов и молекул должен быть настолько небольшим, чтобы их можно было принимать за материальные точки, которые обладают нулевым объемом;
- молекулы и атомы не должны взаимодействовать друг с другом.
Получается, что идеальный газ является совокупностью материальных точек, которые движутся в хаотичном порядке. Скорость и масса обуславливают температуру всей газовой смеси. Давление, что вещество оказывает на сосуд, зависит от температуры, количества молекул и объема самого сосуда.
Для идеального газа будет справедливо такое уравнение:
\(PV=nRT\)
Данное уравнение носит название уравнения состояния. Оно является объединителем давления (то есть P), температуры (то есть T), объема (то есть V), а также числа вещества в молях (то есть n). Значение R является коэффициентом пропорциональности, равный 8,314 Дж/К моль.
Интересно, что в данном уравнении нет ни одной величины, которая бы зависела от химического характера атомов и молекул. Идеальные газы — практически все газы или газовые смеси, температура и давления которых не слишком низкая и не слишком большая соответственно.
Иная формулировка закона Дальтона
Закон Дальтона для газовой смеси возможно выразить не только через парциальное давление, но и через мольные доли каждого из элементов. Так получится соответствующая формула. Так как каждый элемент газовой смеси обладает независимым характером от иных в смеси газов, для него возможно записать такое уравнение состояния:
\(P_{i}V=n_{i}RT\)
Данное уравнение будет верным для всех i элементов, потому что их температура и объем будут одинаковыми. Значение \(n_{i}\) является количеством молей элемента i газовой смеси.
Выразим теперь парциальное давление, и разделим его на полное давление всей смеси, тогда получим:
\(\frac{P_{i}}{P_{tot}}=\frac{n_{i}RT}{V}=\frac{V}{nRT}=\frac{n_{i}}{n}\)
Тут n будет общим числом элементов в газовой смести. Эти значение можно получить при условии суммирования всех \(n_{i}\). Соотношение \(\frac{n_{i}}{n}\) будет носить название мольной доли компонента i в газовой смеси. Часто обозначают как \(x_{i}\).
Через мольные доли возможно записать закон Дальтона так:
\(P_{i}=P_{tot}\times{x_{i}}.\)
Мольную долю представляют в виде атомных процентов элементов газовой смеси. К примеру,21 % \(O_{2}\) в воздухе сообщает то, что сольная доля кислорода равняется 0,21. То есть каждая пятая молекула воздуха будет кислородом.
Применение закона Дальтона в случае решения задач
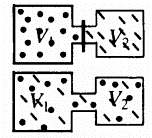
Одной из самых популярных задач на закон Дальтона можно считать задачу, в условиях которой газы расположены в сосудах, которые соединяются трубкой с краником. По условиям задачи необходимо найти давление, которое установится после открытия крана.
После того, как кран будет открыт, первый и второй газы заполнят все пространство обоих сосудов. Нужно использовать закон Бойля-Мариотта для первого газа, потому что температура будет постоянной:
\(p_{1}V_{1}\rightarrow\acute{p}_{1}(V_{1}+V_{2})\)
\(\acute{p}=\frac{p_{1}V_{1}}{V_{1}+V_{2}}\)
Данный закон возможно использовать и для другого газа. Получится:
\(\acute{p_{2}}=\frac{p_{2}V_{2}}{V_{1}+V_{2}}.\)
При помощи закона Дальтона получится такое соотношение:
\(p=\acute{p}_{1}+\acute{p}_{2}=\frac{p_{1}V_{1}}{V_{1}+V_{2}}+\frac{p_{2}V_{2}}{V_{1}+V_{2}}=\frac{p_{1}V_{1}+p_{2}V_{2}}{V_{1}+V_{2}}\)
Примеры решения задач
Два сосуда соединяются трубкой с краном. Нужно найти величину давления, которое появится после открытия крана. Необходимо считать, что объем второго сосуда в 1,5 раз больше, чем первый. Давление во втором сосуде будет половиной от атмосферного давления. В первом сосуде атмосферное давление меньше в 4 раза.
Решение:
\(V_{2}=1,5V_{1}\),
\(p_{2}=4p{1}\),
\(p_{2}=10^5Па\).
Применим формулу: \(\frac{p_{1}V_{1}+p_{2}V_{2}}{V_{1}+V_{2}}=\frac{\frac{p_{2}}{4}V_{1}+1,5p_{2}V_{1}}{V_{1}+1,5V_{1}}\). Нужно преобразовать уравнение, найти давление:
\(p=\frac{V_{1}p_{2}(0,25+1,5)}{2,5V_{1}}=\frac{1,75p_{2}}{2,5}=0,7\times10^5\)
Ответ: \(p=0,7\times10^5 Па.\)
Есть три сосуда, которые содержат разреженный газ. Три сосуда одинаковы, соединяются друг с другом при помощи трубок маленького диаметра: первый сосуд связан со вторым, второй связан с третьим. Изначально давление газа в сосудах составляло p, 3p и p. В процессе исследования открыли и закрыли краник, который соединял второй и третий сосуды, а потом то же сделали с краном первого со вторым сосудом. Нужно найти как изменилось число газа в первом сосуде (увеличилось, уменьшилось, неизменно). Обратите внимание, что температура газа не изменялась.
Решение
- Объемы сосудов являются равными: \(V_{1}=V_{2}=V_{3}=V\).
- Температура равна: \(T_{1}=T_{2}=T_{3}=T.\)
- Давление таково: \(p_{1}=p, p_{2}=3p, p_{3}=p\).
После открытия крана между 2 и 3 объем элементов увеличился в два раза, давление распределилось равномерно. По закону Дальтона давление стало равно сумме давлений, которые оказываются газами в размере вещества \(V_{2}\) и \(V_{3}\). Из-за того, что объем увеличился в два раза, парциальное давление будет равно половине изначального давления:
\(p_{23}=\frac{p}{3}=\frac{3p}{p}=2p\).
Посмотрим, что было, когда открыли кран 1 и 2. \(p_{12}=\frac{2p}{2}=\frac{p}{2}=\frac{3p}{p}\).
Используем закон Клайперона-Менделеева: \(pV=vRT\). Для изначального характера газа в первом сосуде: \(pV=v_{1}RT\). Конечное состояние в первом сосуде: \(\frac{3p}{2}V=v_{2}RT\).
Из-за неизменности температуры и объема, но изменении давления в 1,5 раз больше, величина газа в первом сосуде стала больше в 1,5 раза.
Ответ: увеличилось в 1,5 раза.
В сосуде объема, который не изменился, при комнатной температуре находилась смесь аргона и неона (1 моль каждого). Половина сосуда была выпущена, а потом в сосуд добавили примерно моль аргона. Рассчитайте, как поменялись парциальное давление неона, а также давление газовой смеси, если температура газов в сосуде не изменялась.
Решение:
- Количество неона: \(V_{1}=1 моль\).
- Количество аргона: \(V_{2}=1 моль\).
- Количество аргона, который впустили: \(V_{4}=1 моль\).
Изначально парциальное давление аргона и неона было равным. Это можно объяснить тем, что давление газов будет зависеть от температуры и объема при неизменном числе элементов газовой смеси. Данные величины являются постоянными. Когда из сосуда выпустили часть газовой смеси, в нем оказалось по половине моля каждого из газов. Потом добавили еще 1 моль аргона. Значит, что в сосуде теперь содержится 0,5 моль неона, а также 1,5 моля аргона. Записываем уравнение Клайперона-Менделеева: \(pV=vRT\).
Из данного уравнение видно, что количество и давление вещества являются прямо пропорциональными величинами. Значит, если количество неона стало меньше, то его парциальное давление уменьшилось. Общая сумма количества вещества будет равно сумме количества вещества 1 неон и 2 аргона: 0,5+1,5=2 (моль). Сначала в сосуде было 2 моль газа. Из-за того, что количество вещества, объема и температуры сохранились, давление — не изменилось.
Ответ: Парциальное давление неона уменьшилось. Давление смеси газов в сосуде не изменилось.
В сосуде объемом 10 литров содержится смесь гелия и водорода. Масса смеси — 2 грамма при температуре 27 градусов по Цельсию, а также давлении 200 кПа. Какое отношение будет массы водорода к массе гелия в составе газовой смеси?
Решение:
Записываем уравнение Менделеева-Клапейрона для гелия и водорода в газовой смеси:
\(pH_{2}V=\frac{mH_{2}}{\mu{H_{2}}}RT\)
\(pH_{e}V=\frac{mH_{e}}{\mu{H_{e}}}RT\)
По закону Дальтона давление смеси будет таким:
\(p=pH_{2}+pH_{e}\)
Расчет массы смеси:
\(m=mH_{2}+mH_{e}\)
После решаем систему уравнений:
Ответ: 1,5
В сосуде, объем которого не изменяется, при комнатной температуре находилась смесь гелия и водорода, по 1 моль каждого. Часто содержимого сосуда выпустили, а потом добавили в сосуд 1 моль гелия. Будем считать газы идеальными, температуру в сосуде постоянной. Тогда нужно выбрать утверждения, которые будут соответствовать результаты экспериментов.
- Парциальное давление водорода стало меньше.
- Давление газовой смеси в сосуде стало меньше.
- Концентрация водорода стала больше.
- В начале исследования концентрация водорода была больше гелия.
- В начале исследования масса гелия была больше массы водорода.
Решение
Сначала в сосуде была смесь 1 моль водорода и моль гелия. После того как часть выпустили в сосуде стало 0,5 моль водорода и 0,5 моль гелия. Потом в сосуде появился 1 моль гелия, так в нем стало 0,5 моль водорода, а также 1,5 моль гелия. Температура и объем сосуда являются постоянными.
- Количество водорода стало меньше, парциальное давление стало меньше.
- Общее количество вещества одинаковое (2 моль), давление газовой смеси в сосуде не поменялось.
- Количество водорода стало меньше, концентрация стала меньше.
- В начале исследования количество водорода и гелия было одинаковым, концентрация газов одинаковая.
- Молярная масса гелия была больше, чем у водорода, при условии одинакового количества вещества массы гелия больше.
Значит, что верными являются первое и пятое утверждение.
Ответ: 1,5.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так