Что нужно знать о волновых уравнениях — основные сведения

Содержание:

Содержание

Общий вид волнового уравнения

Волна — возмущения, распространяющиеся в пространстве без транспортировки материи, только энергии. Элемент, который вызывает волны, называется источником. Например, камень, брошенный в воды реки произведут следы круглой формы.

Волны возникают из-за колебаний и колебаний материи. В физике, они известны как волна распространения энергии (а не массы) в пространстве из-за возмущения некоторых из его физических свойств, таких как плотность, давление, электрическое поле или магнитное поле. Это явление может происходить в пустом пространстве или в пространстве, содержащем вещество (воздух, вода, земля и т. д.).

Волны возникают в результате колебаний и колебаний материи, которые распространяются во времени, как описано Теорией волн — ветвью физики, ответственной за понимание этого явления, чрезвычайно распространенного во Вселенной.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В зависимости от происхождения волн или природы среды, через которую они распространяются, будут зависеть эффекты их появления и их характеристики. Таким образом, мы можем говорить о световых, звуковых волнах и т. д., каждая из которых имеет разные физические свойства и частоты, в зависимости, среди прочего, от среды, в которой они распространяются, и от того, сколько энергии они переносят.

Некоторые волны, такие как звуковые, не могут переноситься в вакууме, они требуют физической среды. Другие, такие как электромагнитные волны, могут сделать это идеально и быстро: так работают искусственные спутники, которые передают информацию на Землю с помощью микроволн.

Части волны

Волна состоит из следующих частей:

Гребень. Это пик пульсации.
Долина. Это самая низкая точка волны (противоположность гребня).
Период. Это время, которое требуется волне для перехода от одного гребня к другому, то есть для повторения. Он изображен буквой Т.
Амплитуда. Представляет максимальное изменение смещения, вертикальное расстояние между гребнем и средней точкой волны. Он изображен буквой А.
Частота. Это количество раз, когда волна повторяется за определенную единицу времени, поэтому она рассчитывается по формуле f = 1 / T. Он изображен буквой f.
Длина волны. Это расстояние между двумя последовательными гребнями пульсации. Он представлен символом λ (lamda).
Цикл. Это полная рябь, от начала до конца.

Как распространяются волны

Электромагнитные волны не требуют материальной среды для распространения. Волны обычно нуждаются в материальной среде для распространения, хотя некоторые из них могут отлично работать в вакууме (в зависимости от характера волны). Например, электромагнитные волны, которые представляют собой колебания электрических и магнитных полей и движутся со скоростью света, не требуют материальной среды для распространения.

Вместо этого для распространения механических волн требуется физическая среда, например вода, металл или воздух. Например, когда мы бросаем камень в пруд, камень вызывает волну, которая распространяется по воде.

Волновое уравнение

Волновое уравнение представляет собой линейное дифференциальное уравнение в частных производных второго порядка, которое описывает распространение колебаний с фиксированной скоростью в некоторой величине y:

Решение волнового уравнения в двух измерениях, распространяющегося по фиксированной области:

Формула 1

$(1/v2)*(∂2y/∂t2)=(∂2y/∂x2),$

где v — скорость волны.

Это уравнение является хорошим описанием для широкого спектра явлений, поскольку оно обычно используется для моделирования небольших колебаний относительно равновесия, для которых системы часто могут быть хорошо аппроксимированы законом Гука. Решения волнового уравнения, конечно, важны в гидродинамике, но также играют важную роль в электромагнетизме, оптике, гравитационной физике и теплопередаче. Особенно важны решения преобразования Фурье волнового уравнения, которые определяют ряды Фурье, сферические гармоники и их обобщения.

Вывод волнового уравнения

Вывод волнового уравнения варьируется в зависимости от контекста. Особенно простая физическая установка для вывода — это небольшие колебания на куске струны, подчиняющиеся закону Гука. Рассмотрим приведенную ниже диаграмму, показывающую кусок струны, смещенный на небольшую величину от равновесия:

Небольшие колебания струны (синий). На небольшом элементе массы, содержащемся в небольшом интервале dx, напряжения T и T' тянут элемент вниз.

Рассмотрим силы, действующие на небольшой элемент массы dmdm, содержащийся в небольшом интервале dx. Если смещение невелико, то горизонтальная сила приблизительно равна нулю. Вертикальная сила равна:

Формула 2

$∑Fy = -T'sinθ2 -T'sinθ1 = (dm) a = μdx(∂2y/∂t2),$

где μ — плотность массы μ=∂х/∂м из струны.

С другой стороны, поскольку горизонтальная сила приблизительно равна нулю при малых перемещениях, $Tcosθ1 ≈ Т′cosθ2 ≈ T$. Следовательно,

$-(μdx ∂2y/∂t2)/T ≈ (T′sinθ2+Tsinθ1)/T = (T′sinθ2/T) + (Tsinθ1/T) ≈ (T′sinθ2/T′cosθ2) + (Tsinθ1/Tcosθ1) = tanθ1+tanθ2.$

Однако $tanθ1 + tanθ2 = -Δ∂x/∂y$, где разница между x и x+dx. Это происходит потому, что касательная геометрически равна наклону. Деля на dx, можно найти

$-(μ∂2y/∂t2)/T = (tanθ1+tanθ2/dx) = - (Δ∂y/∂x)/dx)).$

Крайний правый член уравнения выше — это определение производной по отношению к x, поскольку разница находится на интервале dx, и, следовательно, имеет вид:

$(μ/T)(∂2y/∂t2) = ∂2y/∂x2,$

что в точности соответствует волновому уравнению в одном измерении для скорости $v = \sqrt{\frac{T}{\mu}}v=μT$.

Многие выводы для физических колебаний аналогичны. Ниже приведен вывод для волнового уравнения для света, в котором используется совершенно другой подход.

Неоднородное уравнение

Неоднородное волновое уравнение выглядит следующим образом:

Формула 3

$∂2u/∂t2=v2Δu+f,$

где: функция f=f(x,t) выражает воздействие внешней силы.

Решение волнового уравнения

Уравнение волны и волновое уравнение, решение

Все решения волнового уравнения являются суперпозициями «движущихся влево» и «движущихся вправо» волн, f(x+vt) и g(x-vt). Они называются перемещающимися влево и вправо, потому что, хотя общая форма волны остается постоянной, волна перемещается влево или вправо во времени. Кроме того, любые суперпозиции решений волнового уравнения также являются решениями, поскольку уравнение линейно.

Примечание 1

Суперпозиция — это способность квантовой системы находиться в нескольких состояниях одновременно до тех пор, пока она не будет измерена. Поскольку концепцию трудно понять, этот важнейший принцип квантовой механики часто иллюстрируется экспериментом, проведенным в 1801 году английским физиком Томасом Янгом. Эксперимент Юнга с двумя щелями был призван доказать, что свет состоит из волн.

Доказать, что все решения волнового уравнения являются суперпозициями «движущихся влево» и «движущихся вправо» волн.

Определите новые координаты $a = x - vt$ и $b=x+vt$, представляющие правое и левое распространение волн соответственно. Тогда частные производные могут быть переписаны как:

$(∂/∂x) = 1/2 (∂/∂a+∂/∂b) → (∂2/∂x2) = 1/4 (∂2/∂a2 + 2(∂2/∂a∂b) + (∂2/∂b2));$

$(∂/∂е) = v/2 (∂/∂b+∂/∂a) → (∂2/∂t2) = v2/4 (∂2/∂a2 - 2(∂2/∂a∂b) + (∂2/∂b2)).$

Поскольку волновым уравнением является:

$∂2y/∂x2 - (1/v2)(∂2y/∂t2)=0,$

подставляя в для частных производных, получаем уравнение в координатах a и b:

$∂2y / ∂a∂b = 0.$

Это решается в общем случае $y = f(a) + g(b) = f(x-vt) + g(x+vt) y = f(a) +g(b) = f(x−vt) + g(x+vt)$, как заявлено.

Формула Д'Аламбера

Метод Д'Аламбера обеспечивает решение одномерного волнового уравнения:

Формула 4

$∂2y/dx2 = (1/c2)(∂2y/dt2).$

Это моделирует колебания струны. Общее решение может быть получено путем введения новых переменных: $ξ=x-ct$ и $η=x+ct$, применяем правило цепочки для получения:

$(∂/∂x) = (∂ξ/∂x)(∂/∂ξ) + (∂η/∂x)(∂/∂η) = (∂/∂ξ)+(∂/∂η);$

$(∂/∂t)=(∂ξ/∂t)(∂/∂ξ)+(∂η/∂t)(∂/∂η)=-c(∂/∂ξ+c/∂η).$

Соответственно, это расширение уравнения затем дает:

$∂2y/∂ξ∂η=0.$

Формула Кирхгофа

Формула дифракции Кирхгофа может быть использована для моделирования распространения света в широком диапазоне конфигураций либо аналитически, либо с использованием численного моделирования. Это дает выражение для волнового возмущения, когда монохроматические сферические волны являются входящей волной рассматриваемой ситуации. Эта формула получена путем применения интегральной теоремы Кирхгофа, которая использует второе тождество Грина для получения решения однородного скалярного волнового уравнения для сферической волны с некоторыми приближениями.

Принцип Гюйгенса–Френеля выводится с помощью формулы дифракции Френеля-Кирхгофа.

Формула 4

Формула 5 — Источник: hep.manchester.ac.uk

где:

U — это пространственная часть решения однородного скалярного волнового уравнения, (т.е. V(r,t)=U(r)e^iwt как решение однородного скалярного волнового уравнения), k — волновое число, а s — расстояние от P до (бесконечно малого) интегрального элемента поверхности, и ∂/∂n обозначает дифференцирование вдоль единичного вектора нормали элемента интегральной поверхности т.е. ∂f/∂n = ∇f*n.

Обратите внимание, что нормаль поверхности или направление n в этом интеграле направлено внутрь замкнутого объема; если используется более обычная нормаль, указывающая наружу, интеграл будет иметь противоположный знак. А также обратите внимание, что в показанной здесь интегральной теореме n и P являются векторными величинами, в то время как другие члены являются скалярными величинами.

Для приведенных ниже случаев делаются следующие основные допущения:

Расстояние между точечным источником волн и интегральной областью, расстояние между интегральной областью и точкой наблюдения P и размер отверстия S намного больше, чем длина волны λ.
U и ∂U/∂n = ∇U*n являются прерывистыми на границах отверстия, называемыми граничными условиями Кирхгофа. Это может быть связано с другим предположением о том, что волны на отверстии (или открытой области) совпадают с волнами, которые присутствовали бы, если бы для волн не было препятствий.

Формула Пуассона

Уравнение Пуассона — это эллиптическое дифференциальное уравнение в частных производных, имеющее широкое применение в теоретической физике.

Например, решением уравнения Пуассона является потенциальное поле, вызванное заданным распределением электрического заряда или плотности массы; зная потенциальное поле, затем можно рассчитать электростатическое или гравитационное (силовое) поле. Это обобщение уравнения Лапласа, которое также часто встречается в физике. Уравнение названо в честь французского математика и физика Симеона Дени Пуассона.

Уравнение Пуассона имеет вид:

Формула 6

Δφ=f,

где Δ — оператор Лапласа, а φ и f вещественные или комплекснозначные функции на многообразии. Обычно f задается, а ищется φ. Когда многообразие является евклидовым пространством, оператор Лапласа часто обозначается как ∇2, и поэтому уравнение Пуассона часто записывается как:

∇²φ=f.

В трехмерных декартовых координатах оно принимает вид:

$(∂2/∂x2+∂2/∂y2+∂2/∂z2)φ(x,y,z).$

Когда f = 0 идентично, мы получаем уравнение Лапласа.

Уравнение Пуассона может быть решено с помощью функции Грина:

E = ρ/ϵ0 дает уравнение Пуассона $∇2Φ = −ρ/ϵ0.$

где интеграл находится по всему пространству. Общее изложение функции Грина для уравнения Пуассона приведено в статье, посвященной экранированному уравнению Пуассона. Существуют различные методы численного решения, такие как метод релаксации, итерационный алгоритм.

Особенности и методы решения волновых уравнений

Наиболее часто используемыми примерами решений являются гармонические волны:

$y(x,t) = A \sin (x-vt) + B \sin (x+vt) ,$
$y(x,t)=Asin(x−vt)+Bsin(x+vt),$

где y0 — это амплитуда волны, а A и B являются некоторыми константами, зависящими от начальных условий.

Если условия таковы, что решения принимают одинаковое значение в обеих конечных точках, решения могут привести к появлению стоячих волн, как показано выше. Они принимают функциональную форму:

$y(x,t) = y_0 \sin (x-vt) + y_0 \sin (x+vt) = 2y_0 \sin(x) \cos (vt),$
$y(x,t)=y0;$

$sin(x−vt)+y0;$

$sin(x+vt)=2y0;$

$sin(x)cos(vt),$

где y0 — это амплитуда волны. Решение имеет постоянную амплитуду, а пространственная часть $ \sin (x) sin(x)$ не зависит от времени.

Условия для волнового уравнения

Формально существует два основных типа граничных условий для волнового уравнения:

Граничные условия Дирихле: Амплитуда фиксируется в граничной точке $x ^{\ast}x∗$. Это может быть записано как:

$y(x∗)=y∗,$

где y^∗ является некоторой фиксированной константой. Более полезным способом написания этого условия является:

$dy/dt ∣ x=x∗=0,$

это говорит о том, что амплитуда в конечной точке не меняется со временем.

Граничные условия Неймана: Производная амплитуды задается в конечных точках. Часто эта производная принимается равной нулю. Для приблизительно безмассовой (очень легкой) струны это означает, что конечные точки свободны, а не фиксированы; для трубы с волнами давления внутри нее это означает, что конечные точки открыты для атмосферы:

$dy/dx ∣ x=x∗=0.$

Строка с граничными условиями Дирихле на левом конце, где строка прикреплена к стене, и граничными условиями Неймана на правом конце, где строка прикреплена к свободно скользящему кольцу.

Примеры решения задач

Задача 1

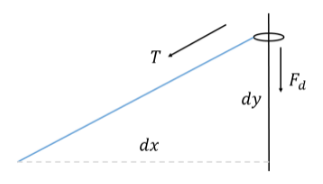
Струна с натяжением T и плотностью массы на единицу длины/мкм прикреплена к небольшому безмассовому кольцу, которое скользит по скользкому стержню. Стержень оказывает демпфирующее усилие Fd= -b*∂y∂t на кольце. Найдите граничное условие для колебаний струны на конце, прикрепленном к кольцу.

Веревка, прикрепленная к кольцу, скользящему по скользкому стержню

Решение:

Кольцо свободно скользит, поэтому граничные условия являются неймановскими, и поскольку кольцо безмассово, общая сила на кольце должна быть равна нулю. Рассмотрим следующую диаграмму свободного тела:

Все вертикально действующие силы воздействуют на кольцо в конце колеблющейся струны

Используя тот факт, что волновое уравнение справедливо только для малых колебаний, dx≫dy. Уравновешивание сил в вертикальном направлении, таким образом, дает:

$-T(∂y/∂х) -b(∂y/∂t) = 0 → ∂y/∂x = -b/T/∂y/∂t.$

Это условие наклона является граничным условием Неймана для колебаний струны на конце, прикрепленном к кольцу.

Задача 2

Дано произвольное гармоническое решение волнового уравнения:

$y(x,t) = A \sin (x-vt) + B \sin (x+vt),$
$y(x,t)=Asin(x−vt)+Bsin(x+vt).$

Найдите общее решение, т.е. найдите коэффициенты A и B при следующих граничных условиях:

$y(0,t) = 0, \qquad y(L,0) = 1$.
$y(0,t)=0,y(L,0)=1.$

Варианты ответа:

$y(x,t) =sin x/sin L;$
$y(x,t) =sin x cos L cos vt;$
$y(x,t) =sin x sin (L-vt);$
$y(x,t) = sin x cos vt / sin L.$

$Решение:$

Один из способов записи решений волнового уравнения генерирует ряды Фурье, которые могут быть использованы для представления функции в виде суммы синусоидальных. Этот метод использует тот факт, что комплексные экспоненты e^-iwtявляются собственными функциями оператора ∂²/∂Т². Используя этот факт, замените решение для конкретного ω:

$y(x,t)=e-iwtf(x),$

где экспоненциальный показатель по существу учитывает зависимость от времени. Подключаясь к волновому уравнению, можно найти:

$∂2y/∂t2=−ω2y(x,t)=v2 (∂2y/∂x2) = v2e -iwt(∂2f/dx2).$

Следовательно, функция f удовлетворяет уравнению:

$∂2f/∂x2=-(w2/v2)f.$

Это решается с помощью плоских волн:

$f(x) = f0e +iwx/v.$

Следовательно, общее решение для конкретного $ω$ может быть записано как:

$y(x,t) = f0ei(w/v)(x±vt).$

Это согласуется с приведенным выше утверждением о том, что решения записываются как суперпозиции f(x-vt) f (x−vt) и g (x + vt) g (x + vt) для некоторых функций f и g. Благодаря линейности волнового уравнения произвольное решение может быть построено в терминах суперпозиций вышеуказанных решений, которые имеют фиксированный $ω$ . Это именно утверждение о существовании ряда Фурье.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»