Сила упругости в физике
Сила упругости — определение
В реальных условиях в окружающем мире человек постоянно наблюдает действие различных сил на какие-либо посторонние предметы и непосредственно на себя. Когда какая-либо сила оказывает воздействие на объект, по этой причине он сам, либо некоторые его компоненты, приводятся в движение. Существует множество видов такого движения. К примеру, если определенная часть материального тела перемещается в некотором направлении относительно остальных составляющих частей, можно наблюдать, как в процессе меняются форма и габариты рассматриваемого объекта. У данного явления имеется научное определение.
Деформация представляет собой смену взаимозависимого расположения частиц материального тела, сопровождающееся их движением по отношению друг к другу, что является следствием воздействия приложенной силы, которая способствует изменению формы и габаритов этого объекта.
Перечислим наиболее простые разновидности деформации:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- растяжение;
- сжатие;
- сдвиг;
- сгибание;
- кручение.
В зависимости от характера и производимого эффекта деформационные изменения классифицируют следующим образом:
- упругая, то есть деформация, которую представляется возможным обратить;
- неупругая, либо необратимые деформационные воздействия.
Упругой называют деформацию, при которой материальный объект возвращается к исходной форме и габаритным размерам, когда прекращают действие деформирующие его силы.
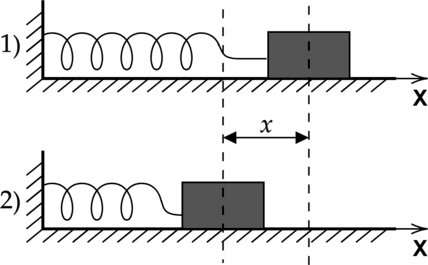
Рассмотрим несколько типичных примеров реализации на практике упругой деформации. Если согнутую линейку отпустить, то есть прекратить силовое воздействие на этот предмет, можно наблюдать, как она выпрямится и примет начальную прямую форму. Растянутая пружина сжимается обратно, когда прекращается растяжение. Смятый в руках шарик, наполненный воздухом, восстановится сразу, как только его отпустить.
Таким образом, проявляется обратимость перечисленных деформаций. Рассмотрим обратный вариант проявления этой особенности. Предположим, что к предмету приложена чрезмерно большая сила. Если очень сильно сгибать линейку, то в зависимости от физико-технических характеристик материала, используемого при изготовлении, через некоторое время она сломается. Аналогично и с другими объектами, то есть пружина не сможет вернуть начальную упругую форму, а шарик вовсе утратит форму и лопнет от значительного сжатия в руках.
Описанные ранее свойства материалов восстанавливаться, либо утрачивать первоначальные характеристики, активно изучают в физике, химии, инженерии. Данные параметры учитывают при проектировании зданий и сооружений. С помощью испытаний и точных расчетов специалисты определяют параметры конструкций такие, которые позволяют им противостоять упругим деформациям. При этом необратимые деформационные воздействия должны быть исключены при заданных условиях эксплуатации для обеспечения безопасности и долговечности построек.
Сила упругости представляет собой такую силу, под действием которой материальные тела возвращают начальную форму и габаритные размеры, измененные в результате упругой деформации, что обеспечено посредством взаимодействия частиц рассматриваемого объекта на уровне молекул и атомов.
В чем измеряется, формула
В процессе своего воздействия на материальное тело сила упругости уравновешивает силы, действующие на предмет извне, по направлению противоположно смещению частиц, то есть:
- когда тело растягивается, сила упругости способствует сжатию;
- в процессе сжатия возникает сила упругости, которая стремится придать предмету изначальное прямое состояние.
Исходя из вышесказанного, можно сделать вывод о том, что сила упругости прямо пропорциональна деформации, что допустимо выразить следующим математическим соотношением:
\(F_{\text{упр}}\sim\Delta l\)
Отношение силы упругости к деформационным изменениям, если упругие деформации минимальны, справедливо выразить, как постоянную величину:
\(k=\frac{F_{\text{упр}}}{\Delta l}=const\)
Записанное значение обозначает коэффициент упругости или жесткости, который измеряется в Ньютонах на метр, то есть \(\frac{Н}{м}\) . В свою очередь, сила упругости, как и прочие подобные величины, измеряется в Ньютонах, то есть Н. С целью количественного определения силы упругости используют динамометр.
Динамометр представляет собой прибор, с помощью которого измеряют величину силу упругости.
Обычный прибор включает в себя пружину, дополненную крючком, и дощечки со шкалой единиц, проградуированной в Ньютонах. Значение, на которое удлинилась пружина, относится прямо пропорциональным к силе, воздействующей на предмет. С возрастанием этой силы можно наблюдать, как увеличивается удлинение пружинного механизма. В процессе измерения стрелка, перемещаясь по шкале, демонстрирует, какое значение принимает сила. Существуют разные модификации динамометров, к примеру, оборудование промышленного назначения. Однако принцип действия у подобных устройств не отличается.
Закон Гука
Закон Гука: абсолютное значение силы упругости прямо пропорционально величине деформационного изменения, то есть:
\(F = k \cdot x\)
Здесь k обозначает коэффициент жесткости, определение которого было дано ранее.
Источник: physics.shkolkovo.net
Примеры решения задач
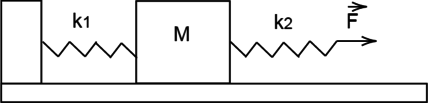
На рисунке ниже изображен некоторый предмет кубической формы весом 3 кг. Данный объект ввели в систему, состоящую из пары пружин, на которую воздействует внешняя сила величиной 20 Н в горизонтально ориентированном направлении. Пружинные механизмы обладают жесткостью 400 Н/м и 800 Н/м соответственно. Нужно вычислить, насколько удлинилась первая пружина при условии, что система пребывает в состоянии покоя, и трение между рассматриваемым предметом и его опорой имеет нулевое значение.
Источник: physics.shkolkovo.net
Решение
В данном случае целесообразно обратиться к закону Гука. С помощью уже знакомой из теоретического материала формулы потребуется выразить величину, на которую увеличена пружина, подставить численные значения из условия задания и рассчитать искомую величину:
\(\triangle x = \frac{F}{k_{1}} = \frac{20}{400} = 0,05 (м) = 5 (см)\)
Ответ: 5 см.
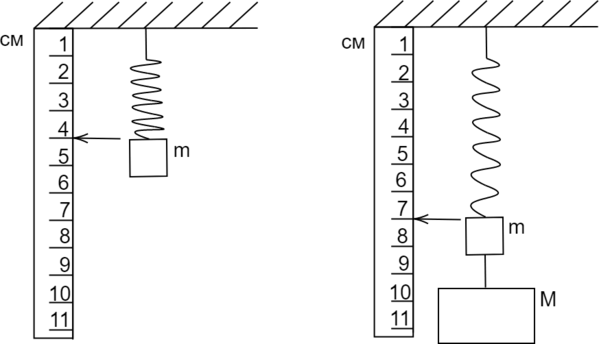
На небольшом предмете, масса которого равна m, зафиксировали некий подвес весом М. Перечисленные действия привели к растяжению пружины жесткостью 1200 Н/м, что демонстрирует изображение. Нужно определить массу М подвешенного груза, выраженную в килограммах, при ускорении свободного падения в \(10 м/с^{2}\).
Источник: physics.shkolkovo.net
Решение
В первую очередь целесообразно смоделировать ситуацию, когда предмет массой m находится в состоянии покоя. Тогда на объект оказывают воздействие пара противоположных сил, то есть тяжести и упругости. Запишем первый закон Ньютона, справедливый для рассматриваемой системы:
\(mg = F_{упр1}\)
После того, как к предмету прикрепили дополнительный груз, ситуация поменялась. В результате сформировалась система, которую допустимо описать с помощью первого закона Ньютона с такой формулировкой:
\(mg+ Мg = F_{упр2}\)
Далее запишем закономерность для силы упругости, то есть закон Гука:
\(F_{упр} = kх\)
Подставим это математическое соотношение в выражения, записанные ранее. В результате получим:
\(mg = kx_{1}\)
\(mg + Mg = kx_{2}\)
Путем вычитания из первого выражения второго получим следующее справедливое равенство:
\(Мg = k(x_{2} - x_{1}) \Rightarrow M = \frac{k(x_{2} - x_{1})}{g} = \frac{1200\cdot 0,03}{10} = 3,6 (кг)\)
Ответ: 3,6 кг
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так