Момент силы в физике
Момент силы — это
С моментом силы нередко встречаются в процессе решения задач на нахождения различных величин, описывающих перемещение какого-либо тела. Смысл данного понятия заключается в характеристике вращения объекта вокруг собственной оси. Рассчитывают искомую величину путем определения результата от умножения силы, оказывающей воздействие на движущийся предмет, и расстояния, на которое удалена ось вращения от точки приложения усилия. Теоретические принципы и практические навыки подсчета момента силы применяют в разных сферах научной и инженерной деятельности.
Момент силы представляет собой величину в физике, характеризующую вращательное действие силы на материальное тело. Момент силы равен произведению усилия на расстояние между осью вращения и точкой, к которой приложена рассматриваемая сила.
Из формулировки понятия можно сделать вывод о наличии прямой связи между моментом силы и вращением объекта, а также зависимости величины от степени оказываемого воздействия. Таким образом, при повышении прикладываемого усилия, направление которого является перпендикуляром к оси вращательного движения, и увеличения отрезка между осью и точкой приложения воздействия, наблюдается рост значения момента силы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В повседневной жизни люди часто сталкиваются с таким физическим понятием как момент силы. К примеру, если открыть дверь путем приложения усилия к ручке, формируется момент силы, способствующий вращательному передвижению створки по круговой траектории относительно оси. Когда мастер откручивает гайку с помощью специального ключа, вращение инструмента образует момент силы, обеспечивающий установку или демонтаж гайки.
В чем измеряется
Размерность величины момента силы допустимо сформулировать, как «сила, помноженная на расстояние». В системе единиц измерения СИ параметр переводят в ньютон-метры. В результате получим, что 1 \(Н\cdot\)м соответствует такому моменту, который образуется усилием, равным 1 Н, на рычаг размером 1 м. При этом точка приложения силы совпадает с концом рычажного устройства, а направление воздействия перпендикулярно относительно рычага. В теории размерность \(\vec {M} (Н\cdot м)\) аналогична параметрам энергии и работы в механике с формальной точки зрения.
Как найти: формула
В физике предусмотрены прикладные формулы для вычисления момента силы, применительно к разным ситуациям. В том случае, когда воздействие направлено перпендикулярно относительно оси вращательного движения, момент силы вычисляют с помощью следующего математического соотношения:
\(М = F \cdot r\)
В формуле М представляет собой момент силы, F выражает величину усилия, r обозначает расстояние от оси, вокруг которой перемещается объект, до точки приложения силы.
Существует общее уравнение, выражающее момент силы \( \vec{F}\), воздействующей на объект, в формате векторного произведения:
\(\vec {M}=\left[{\vec {r}}\cdot {\vec {F}}\right]\)
В записанном выражении \(\vec {r}\) обозначает радиус-вектор точки, куда приложено усилие. Вектор силового момента расположен перпендикулярно относительно \(\vec {r} и \vec{F}\). Радиус-вектор отмеряют от некоторой точки. В распространенных ситуациях выбирают участок, где зафиксирован подвес для вращающегося тела, или отметку на оси вращения рассматриваемого объекта.
Математическая закономерность неизменности момента силы подразумевает нулевое значение для суммы моментов, которые сформированы усилиями, действующими внутри изучаемой системы при отсутствии влияния сторонних сил. Запись закона сохранения моментов сил: \(\sum M = 0\)
Озвученное правило применяют в механике для анализа и прогнозирования изменений в наблюдаемых системах, образованных вращающимися объектами. В качестве примера таких систем можно привести колесо велосипеда. В процессе воздействия велосипедиста на педали формируется момент силы, способствующий вращению колеса. Исходя из положений приведенной закономерности, суммарная величина моментов, возникающих внутри колеса, характеризуется постоянным значением, что необходимо для продолжения вращательного движения.
Примеры решения задач
К некоторому рычагу приложено усилие, создающее момент в \(20 Н\cdot м\). Известно, что рычажный механизм пребывает в равновесном положении, а оказываемое на него воздействие равно 5 Н. Требуется вычислить значение плеча силы.
Решение
Заметим, что из условия задания известны величины момента силы и воздействия. Исходя из равновесного состояния рассматриваемой системы, следует применить закон сохранения момента силы. Сформулируем математическую закономерность:
\(М_{1} = М_{2}\)
В результате справедливой является формула для определения первого момента силы:
\(М_{1} = F_{2} \cdot l_{2}\)
Выразим плечо второго усилия из записанного выше уравнения. Путем подстановки заданных по задаче величин рассчитаем искомый параметр и запишем ответ:
\(l_{2} = \frac{20}{5} = 4\)
Ответ: плечо второй силы составляет 4 м.
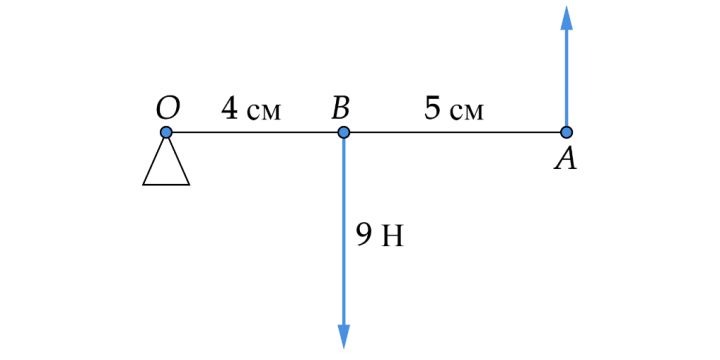
Рычажный механизм испытывает воздействие сил, пространственная ориентация которых продемонстрирована на схематичном изображении. Модуль силы, действующей на некоторую точку, отмечен на рисунке. За точку следует принять ось вращательного передвижения рычага. Нужно вычислить значение приложенного к отметке усилия при условии нахождения рассматриваемой системы в равновесном состоянии.
Источник: 3.shkolkovo.online
Решение
По определению закономерности сохранения моментов сил суммарная величина таких характеристик соответствует нулевому значению. Составим соответствующее соотношение:
\(F_{B}\cdot OB = F_{А}\cdot ОА\)
Выразим из уравнения \(F_{А}\)через известные из условия задания величины:
\(F_{А} = \frac{F_{B}\cdot OB}{ОА}\)
С помощью подстановки числовых значений найдем искомую силу, приложенную к рычагу:
\(F_{А} = \frac{9\cdot 4}{4+5} = 4\)
Ответ: 4 Н.
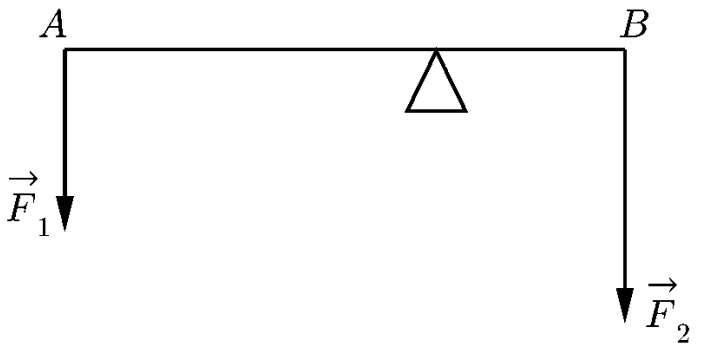
Равновесная система сформирована в рычажном механизме, на который оказывает влияние пара сил. Направленное усилие \(F_{2}\) соответствует 6 Н. Плечо силы \(F_{1}\) равно 25 см. Плечо силы \(F_{2}\) меньше и составляет 15 см. Требуется вычислить значение силы \(F_{1}\).
Источник: 3.shkolkovo.online
Решение
Из условий задания можно сделать логичное заключение о равновесном состоянии рычага, когда сумма моментов сил обладает нулевым значением. Выразим моменты первого и второго усилия, чтобы записать справедливое равенство:
\(F_{1} \cdot l_{1} = F_{2} \cdot l_{2}\)
С помощью записанного выражения несложно представить формулу расчета для первой силы:
\(F_{1} = \frac{F_{2} \cdot l_{2}}{l_{1}}\)
Остается подставить числовые значения заданных величин и записать окончательный ответ:
\(F_{1} = \frac{6\cdot 15}{25} = 3,6\)
Ответ: 3,6 Н.
На рычаге в точке В закреплен груз массой 3 кг. В отметке А зафиксирован второй объект. Нужно вычислить вес второго тела при условии соблюдения равновесного состояния полученной системы.
Источник: 3.shkolkovo.online
Решение
В данном случае пригодится закономерность сохранения моментов сил, изученная в теоретическом материале. Если соблюдается равновесие в рассматриваемой системе, то моменты усилий, приложенных к двум точкам, отмеченным на изображении выше, равны. На основании логичных рассуждений сформулируем справедливое равенство для моментов наблюдаемого воздействия на рычажный механизм:
\(m_{B}g \cdot ОВ = m_{х}g \cdot ОА\)
Посчитаем расстояние от точки начала оси вращательного движения рычага до участков, где закреплены грузы. Подставим значения в уравнение:
\(m_{B}g \cdot 4 = m_{х}g \cdot 2\)
Выразим неизвестную массу объекта в точке А. Путем записи известных величин из условия задания рассчитаем, чему равен вес второго груза:
\(m_{х} = 2 m_{B}\)
\(m_{х} = 2 \cdot 3 = 6\)
Ответ: 6 кг.
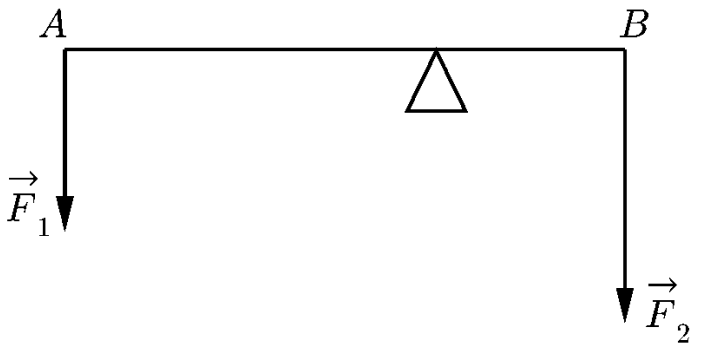
На горизонтально расположенный пруток оказывают воздействие две силы, сохраняя равновесное положение. Усилие \(F_{1}\) соответствует 6 Н. Плечо этой силы равно 15 см. Второе плечо составляет 25 см. Требуется определить значение \(F_{2}\).
Источник: 3.shkolkovo.online
Решение
Описанная по условиям задания система предполагает равновесное состояние стержня. В таком случае допустимо применить закономерность нулевой суммы моментов сил, воздействующих на объект. Между значениями воздействующих усилий целесообразно поставить знак равенства. Запишем соответствующее соотношение:
\(F_{1} \cdot l_{1} = F_{2} \cdot l_{2}\)
При расчете второго плеча усилия следует вычесть из общей длины прута значение первого плеча. С учетом этого условия составим формулу для определения второй силы:
\(F_{2} = \frac{F_{1} \cdot l_{1}}{l_{2}} = \frac{F_{1} \cdot l_{1}}{l - l_{1}}\)
Подставим известные величины и выполним итоговый расчет:
\(F_{2} = \frac{6 \cdot 15}{25 - 15} = 9\)
Ответ: 9 Н.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так