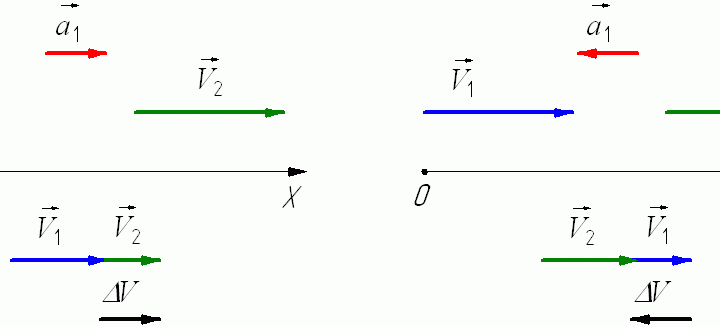Мгновенное ускорение в физике
Мгновенное ускорение — это
Исходя из временного интервала, учитываемого при расчете, ускорение классифицируется как среднее и мгновенное.
Мгновенное ускорение в физике — это ускорение объекта в определенный момент времени во время движения. Оно показывает изменение скорости в единицу времени, измеренное за очень малый промежуток времени dt.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: av-physics.narod.ru
Объект, движущийся по прямой, может испытывать увеличение или уменьшение ускорения, а может двигаться с равномерным ускорением или с нулевым ускорением. Поэтому в таких случаях среднее ускорение не описывает движение объекта в каждый момент времени.
Среднее ускорение дает только среднее значение ускорения, а не фактическое ускорение объекта во время движения. В то время как мгновенное ускорение дает точное значение ускорения в каждый момент времени во время движения.
Единица измерения
Поскольку ускорение — это скорость в метрах, деленная на время в секундах, единицы СИ для ускорения часто сокращенно обозначают м/с2 — то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Это векторная величина. Ее также можно определить, взяв наклон графика «расстояние-время» или графика x-t.
Формула
Мгновенное ускорение определяется как предел среднего ускорения, когда рассматриваемый промежуток времени приближается к 0. Оно также определяется аналогично производной скорости по времени. Оно задается выражением:
a→⃗ = limt→0ΔV→⃗/Δt
где:
a→⃗: ускорение тела,
ΔV→: Вектор изменения скорости,
Δt: Интервал времени, приближающийся к нулю, то есть бесконечно малый интервал.
Как найти
Его можно найти с помощью следующих двух методов:
1. Аналитический метод: этот способ используется для нахождения мгновенного ускорения, когда задано уравнение скорости в терминах времени. Оно может быть решено с помощью метода пределов или дифференцирования.
Используя метод пределов, мгновенное ускорение вычисляется:
aмгн = limΔt→0 (V(t+Δt)-Vt) / Δt
С помощью дифференцирования мгновенная скорость может быть вычислена:
aмгн = dV/dt
2. Графический метод: способ используется для вычисления мгновенного ускорения по графику скорость-время.
Пример а. Если график скорости-времени является линейным.
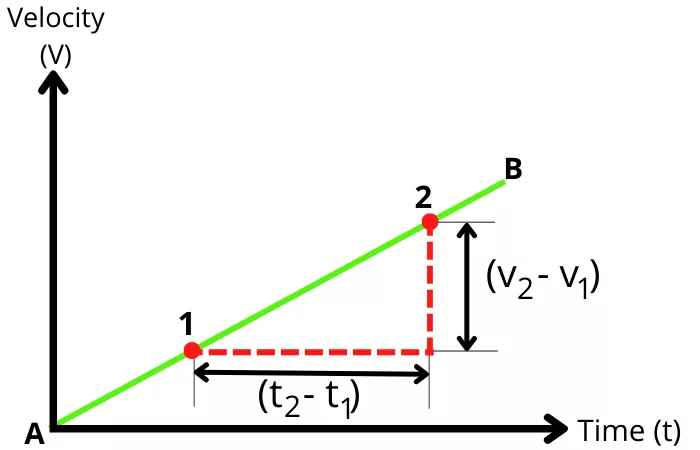
Если график скорости-времени имеет линейный характер, то это означает, что объект движется с постоянным ускорением на протяжении всего своего движения.
Источник: mechcontent.com
Таким образом, в этом случае мгновенное ускорение равно среднему ускорению объекта.
Vмгн = Vср
Vмгн = ΔV / Δt
Vмгн = (V2-V1) / (t2-t1)
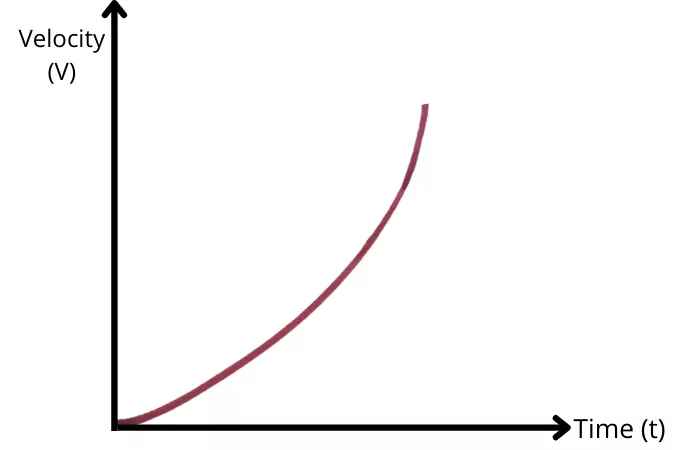
Пример б. Когда профиль скорость-время нелинейный
Если временной профиль скорости нелинеен, это означает, что ускорение объекта меняется на протяжении всего движения.
Источник: mechcontent.com
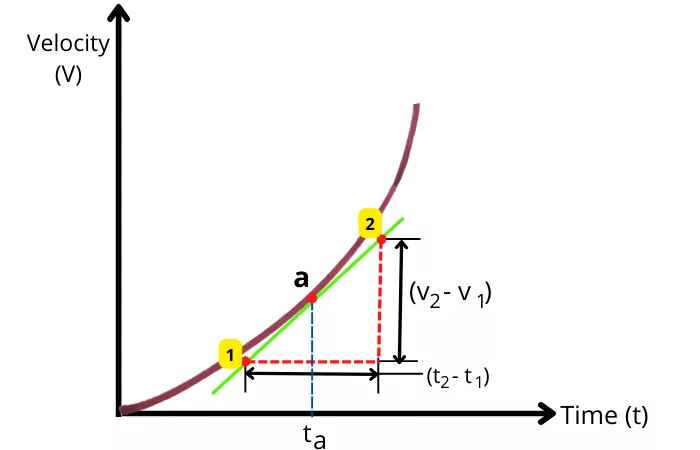
Таким образом, в этом случае мгновенное ускорение объекта отличается от среднего ускорения. По такому графику можно рассчитать мгновенное ускорение, выполнив следующие действия:
- Найти точку кривой в нужный момент времени.
-
В этой точке провести касательную к кривой.
-
Найдите наклон касательной: Мгновенное ускорение — это наклон касательной, проведенной к кривой скорость-время в данный момент.
Источник: mechcontent.com
aмгн = Наклон(1-2) = (V2-V1) / (t2-t1).
Примеры решения задач
Движение автомобиля задается функцией x = 4t2 + 10t + 6. Вычислите его мгновенную скорость в момент времени t = 5 с. Дано: Функция x = 4t2 + 10t + 6.
Дифференцируя заданную функцию по t, получаем:
Vмгн = dx / dt = (d(4t2 + 10t + 6) / (dt)
Для времени t = 5 с мгновенная скорость определяется как:
V(t) = 8t + 10
V(5) = 8(5) + 10
V(5)= 50 м/с.
Ответ: Таким образом, для известной функции мгновенная скорость равна 50 м/с.
Вычислите мгновенную скорость частицы, движущейся по прямой за время t = 3 с с функцией x = 5t2 + 2t + 3? Дано: Функция x = 5t2 + 2t + 3 2t
Разграничивая заданную функцию по отношению к t, получаем мгновенную скорость:
Vмгн = dx / dt = dx / dt = (d(5t2 + 2t + 3) / (dt)
Vмгн = 10t + 2
Для времени t=3 с мгновенная скорость равна V(t)=10t + 2
V(3)=10(3)+ 2
V(3) =32 м/с
Ответ: Мгновенная скорость для данной функции равна 32 м/с.
Частица, вышедшая из состояния покоя, движется со скоростью (6t² + 2t) м/с. Если среднее ускорение частицы равно 6 м/с², то найдите момент времени, когда среднее ускорение равно мгновенному ускорению. Дано: V = (6t2+ 2t) м/с aср = 6 м/с²
Решение:
Мгновенное ускорение частицы задается:
aмгн = dV / dt
aмгн = d / dt(6t2+2t)
aмгн = 12t + 2
Время, в которое Vср равно Vмгн: 6 = 12t + 2
Ответ: t = 0,34 секунды.
Частица движется по прямой со скоростью (5t2+3t)м/с. Каково мгновенное ускорение частицы в момент t = 45,0 с?
Решение: Использование пределов.
Мгновенное ускорение объекта:
at = limΔt→0 V(t+Δt)-Vt / Δt
at = limΔt→0 = [5(t+Δt)2+3(t+Δt)] -[5t2+3t] / Δt
at = limΔt→0 = 5t2+10tΔt+5Δt2+3t+3Δt-5t2-3t / Δt
at = limΔt→0 = 5t2+10tΔt+3Δt / Δt
at = limΔt→0 = 5Δt+10t+3
at = 10t + 3
Ускорение объекта в момент t = 45 секунд определяется по формуле:
a(t=45) = 10(45) + 3
Ответ: a(t=45) = 453 м/с².
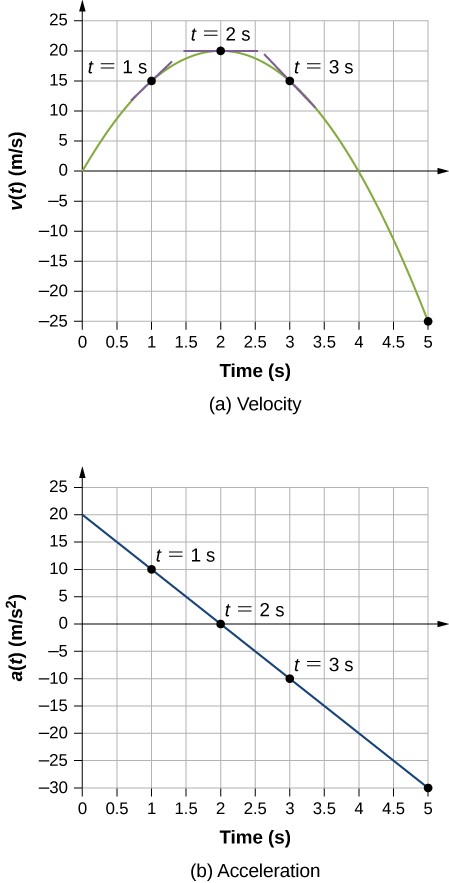
Частица находится в движении и ускоряется. Функциональная форма скорости имеет вид v(t)=(20 м/с)t-(5 м/с2)t2. Найдите функциональную форму ускорения. Найдите мгновенную скорость в моменты времени t = 1, 2, 3 и 5 с. Найдите мгновенное ускорение в моменты времени t = 1, 2, 3 и 5 с.
Интерпретируйте результаты (c) с точки зрения направлений векторов ускорения и скорости.
Найдем функциональную форму ускорения, взяв производную от функции скорости. Затем вычисляем значения мгновенной скорости и ускорения из заданных функций для каждого. Для части (d) нам нужно сравнить направления скорости и ускорения в каждый момент времени.
Решение:
- a(t)=dv(t)dt=(20м/с2)-(10м/с3)t
- v(1s)=15m/s, v(2s)=20m/s, v(3s)=15m/s, v(5s)=-25m/s
- a(1s)=10m/s2, a(2s)=0m/s2, a(3s)=-10m/s2, a(5s)=-30m/s2
- В момент времени t = 1 с скорость v(1s)=15 м/с положительна, а ускорение положительно, поэтому и скорость, и ускорение направлены в одну сторону. Частица движется быстрее.
В момент t = 2 с скорость увеличилась до v(2s)=20 м/с, где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, то есть равен нулю функции ускорения.
При t = 3 с скорость равна v(3s)=15 м/с, а ускорение отрицательно. Частица уменьшила свою скорость, и вектор ускорения отрицателен. Частица замедляется.
При t = 5 с скорость v(5s)=-25 м/с, а ускорение становится все более отрицательным. За время от t = 3 с до t = 5 с скорость частицы уменьшилась до нуля, а затем стала отрицательной, изменив направление движения. Теперь частица снова ускоряется, но уже в противоположном направлении.
Эти результаты мы можем увидеть графически:
Источник: openstax.org
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так