Изотермический процесс: графики, формула, примеры

Какой процесс называется изотермическим

Условием реализации изотермического процесса является наличие в системе термостата. Это крупное тело, которое пребывает в состоянии теплового равновесия. Термостат характеризуется высокой теплопроводностью. В результате повышается скорость обмена теплом с системой по сравнению со скоростью реализации процесса, а также температурный режим в рассматриваемой системе почти равен аналогичным показателем термостата.

Другой вариант осуществления изотермического процесса предполагает использование источников или стоков тепловой энергии. При этом стабилизируется температурный режим с помощью термометров. В качестве изотермических процессов, к примеру, идентифицируют кипящие жидкости и плавление материалов в твердом агрегатном состоянии в условиях стабильного давления. Изотермический процесс изображают в виде изотермы.

Какой закон описывает изотермический процесс

Если на плоскости изобразить координатные линии и обозначить их p и V, то изотермический процесс при переносе на график примет вид гипербол.

Реализация изотермического процесса предполагает приобретение или отдачу системой какого-то объема тепла Q, а также совершение рассматриваемой системой работы А, приложенной к внешним объектам. В другой ситуации при отсутствии теплового обмена с внешней средой система с точки зрения термодинамики пребывает в состоянии уравновешенной энергии, то есть не предусмотрено поглощение или выделение теплоты. Такой процесс называют адиабатическим.

Формула для вычисления работы, которую совершает идеальный газ в процессе изотермии:

\(А = N\,k\,T\,\ln(V_{2}/V_{1})\)

Здесь N отображает количество частиц в газообразном веществе, T характеризует температурный режим, k обозначает постоянную Больцмана, \(V_{1}\) и \(V_{2}\) являются объемами газа, когда процесс только начался, и в его конце.

Материалы в твердом агрегатном состоянии и большинство жидкостей сохраняют стабильность объема, либо минимально его меняют, участвуя в изотермических процессах. Это обстоятельство меняется в случае возникновения фазового перехода.

В результате общий объем тепла, который получила система, тратится на выполнение рассматриваемой системой работы, приложенной к внешним объектам.

Кто открыл изотермический процесс

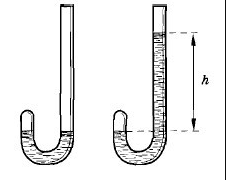
С разницей в 14 лет открытия закона, характеризующего изотермический процесс, совершили Роберт Бойль (1662 г.) и Эдм Мариотт (1676 г.). Наблюдения Бойля над тем, как меняется объем воздушной среды в рамках длинной изогнутой трубки с ртутью.

По наблюдениям Бойля при идентичных уровнях ртути в трубках воздушное давление соответствует значению атмосферному, то есть 760 мм рт. ст. При добавлении ртути в длинное колено емкости Бойль наблюдал уменьшение в два раза объема воздуха при равной разности уровней (h=760 мм). Исходя из этого, имеет место двойное увеличение давления воздуха. Таким образом, ученый пришел к выводу о наличии обратной пропорциональной зависимости между объемом газовой массы и его давлением.

Совершенное открытие было подтверждено многочисленными экспериментальными опытами, которые заключались в анализе изменения системы при увеличении количества ртути в разных пропорциях. Независимо от экспериментальной деятельности Бойля, ученый из Франции Эдм Мариотт сформулировал такую же закономерность. В результате данное соотношение назвали «Закон Бойля-Мариотта».

Формула, графики, уравнение

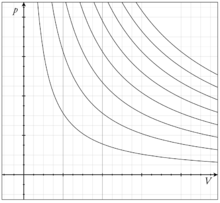
Некоторое количество изотерм для идеального газа нa p-V диаграмме:

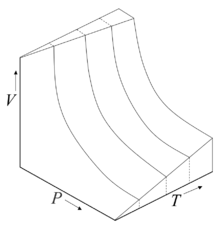
Некоторые изотермы для идеального газа нa p-V-T диаграмме:

Заметим, что при изотермическом процессе масса газообразного вещества не меняется, а температурный режим сохраняет стабильность.

Сформулируем соотношения для пары состояний идеального газа:

\(p_1V_1=\nu RT\)

\(p_2V_2=\nu RT\)

Выполним деление второго уравнения на первое выражение, чтобы получить соотношение изотермического процесса:

\(\frac{p_2V_2}{p_1V_1}=1\)

\(pV=const\)

Процесс состоит в увеличении объема при поступлении теплоты и уменьшении объема при отводе теплоты. С помощью записи первого начала термодинамики выведем соотношение для вычисления  работы, внутренней энергии и количества тепла в случае изотермического процесса:

\(\delta Q=dU+dA=\frac{i}{2}\nu RdT+pdV\)

Стабильность температуры позволяет сделать вывод о нулевом значении изменения внутренней энергии:

\(dU=0\)

Таким образом, общий объем поступающей теплоты в условия течения изотермического процесса расходуется на совершении работы газообразным веществом:

\(\triangle Q=\int\limits^{V_2}_{V_1}{dA}\)

В данном случае \(\delta Q\) является простейшим теплом, которое поступает в систему, dA обозначает простейшую работу, совершаемую газом при изотермическом процессе, i отображает количество степеней свободы молекулы газа, R обозначает универсальную газовую константу, d является количеством молей газа, \(V_1\) представляет собой объем газа в начальный момент, \(V_2\) представляет собой объем газа в конечный момент.

Запишем справедливое равенство, выражающее величину работы:

\(A=\int\limits^{V_2}_{V_1}{pdV}\)

Вычислить давление можно путем выражения его значения из уравнения состояния, в котором пребывает идеальный газ:

\(pV=\nu RT\to p=\frac{\nu RT}{V}\)

Путем объединения полученных выражений получим следующее соотношение:

\(A=\int\limits^{V_2}_{V_1}{\frac{\nu RT}{V}dV}=\nu RT\int\limits^{V_2}_{V_1}{\frac{dV}{V}}=\nu RTln\left(\frac{V_2}{V_1}\right)\)

Воспользуемся законом Бойля-Мариотта:

\(A=\nu RTln\left(\frac{p_1}{p_2}\right)\)

\(\triangle Q=A\)

Таким образом, определено количество тепла, которое получает газ массой m при течении изотермического процесса.

Примеры задач