Изохорный процесс: формула, графики, уравнения

Какой процесс называется изохорным

В термодинамике существует несколько типов процессов, которые могут происходить в условиях, когда масса (m) газов (которые рассматриваются как физический объект для этих исследований) всегда остается постоянной, но иные параметры состояния могут изменяться. Параметры состояния включают давление, объем, температуру и энтропию. Так, в зависимости от того, какой параметр системы сохраняется неизменным, в ходе этого процесса я разделяю четыре их типа: 1) изотермический процесс (низкая или высокая температура сохраняется постоянной), 2) изобарный процесс (разное давление сохраняется постоянным во время всего процесса, выполняемого с системой), 3) изохорный (объем удерживают постоянным на протяжении всего процесса) и 4) адиабатический (постоянная энтропия, то есть отсутствует обмен со средой вокруг физического процесса ни теплом, ни веществом).

Макроскопические тела — это тeла, которые рассматриваются в определении изохорного процесса, обычно включают газы и жидкости. Так, для таких макроскопических тел, если необходимо проводить процесс изохорно, то необходимо нагревать/охлаждать или изменять давление, но при этом соблюдать условие — объем должен оставаться неизменным.

Кто открыл изохорный процесс

Первым, кто проводил испытания над идеальным газом, который использовался как модельная система, при этом были созданы условия в системе, чтобы объем газа оставался постоянны, был французский физик Гийом Амонтон. Первые испытания в такой системе, которые он проводил, были опубликованы им в 1702 году в «Парижских мемуарах». В этой работе были указаны условия проведения данного эксперимента, то есть модель — это идеальный газ, были соблюдены условия, чтобы его объем не менялся, а также важным условием было то, что система была помещена в "стабильный воздушный термометр". В ходе своего эксперимента Амонтон заметил, что при стабильном нагревании давление газа увеличивалось с увеличением T (пропорционально), а жидкость по чуть-чуть вытеснялась веществом в газовой форме и переходила в идущую дальше выступающую колонну, заполняя ее.

Изучение важного для науки изохорного процесса не остановилось на экспериментах Амонтона, его будущее предопределил физик из Англии — Джон Дальтон в 1801 году. Он провел ряд экспериментов, с помощью них удалось выяснить, что при одних и тех же начальных и конечных, т.е. при стабильных давлениях, при варьировании температуры газы сжимаются/расширяются. Третьим важным этапом в изучении интересного изохорного процесса стало овладевание этм процессом французским физиком Жозефом Луи Гей-Люссаком. Он провел собственное независимое исследование, в результате которого эксперименты Далтона ознаменовались как подтвержденыt. А позже Гей-Люссак смог объединить свои выводы с уже известным зависимостью Бойля–Мариотта, именно в результате этой комбинации был подробнейшим образом описан изохорный процесс, где модельной системой является идеальный газ. А правило, описывающее зависимости V газа от T для изохорного процесса было названо в честь исследователя, то есть вторым законом Гей-Люссака. Иное название "закон Шарля" ему дал экспериментатор, приложивший руку к открытию этого уложения, а именно в 1787 году Шарль с помощью эксперимента проверил зависимость давления газа от температуры при поддержании в системе одинакового объема газа, и только после этого в 1802 году Гей-Люссак дополнил этот закон термодинамики.

Условия протекания изохорного процесса

Первым и наиболее важным для реализации процесса — это нахождение ТД системы в замкнутой системе (сосуде или пространстве), чтобы объем в течение всего процесса оставался неизменным. Второе - исследуемое вещество должно находиться в закрытой системе, чтобы не было обмена системы веществом или теплом с окружающей средой (воздухом и т.д.) для простого описания процесса, а также для разработки и вывода более корректных данных. Третьим условием, важным для того, чтобы поток обрабатывался при V = const, является постепенное изменение (повышение/ понижение) градуса в системе.

Формулы, графики, уравнения

\(P\;\sim\;T\)

\(pV\;=\;\frac mMRT\;=\;nRT\), где m — масса газа(кг), M — молекулярная масса газа(кг/моль), R = 8,314 Дж/(моль*К) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

\(\frac{p_1}{p_2}=\frac{T_1}{T_2}\)

Что означает тоже самое, что

\(\frac pT=const\)

То есть отношение давления к температурев ходе всего процесса остается неизменяемым.

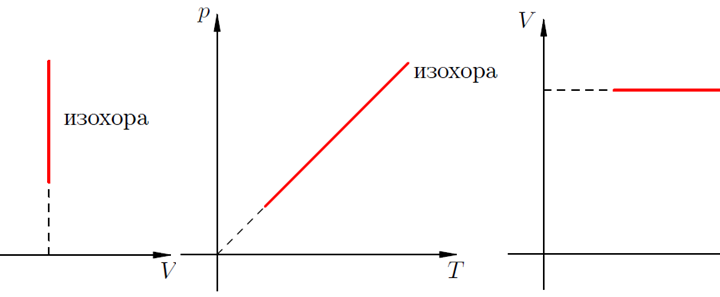
Исходя из того факта, что для изопроцессов с постоянным объемом давление газа в системе прямо пропорционально температуре, то эту зависимость можно представить на графиках для представления. Более того, принято строить графики в разных координатах переменных параметров состояния (давления, температуры и объема), следовательно, существует три типа графиков в разных координатах: p-V, p-T и V-T (рис.1). На любом из этих графиков объем лишается возможным меняться, потому что мы рассматриваем изохорный процесс, а линия графика зависимости называется изохорой.

Рис.1. Графики зависимостей для изохорного процесса в различных координатах.

Количество теплоты при изохорном процессе

Определяется из I Закона ТД, который звучит следующим образом (пока что без наложения условия, что объем газа неизменный), а также при условии, что работу делает сама система, а не внешние силы над системой:

Количество теплоты, полученное системой, расходуется на изменение внутренней энергии и совершения системой работы над внешними силами (телами и т.д.)

\(\triangle U= Q — A \)

Когда мы работаем в системе с стабильным объемом, то есть протекает изохорный процесс, то I начало термодинамики приобретает некоторые ограничения, первое из которых — это то, что работа, которую совершает система в изохорном процессе, будет равна нулю:

\(A\;=\;p\ast\triangle V\;=0\)

Таким образом, работа в ходе изопроцесса с постоянным объемом не совершает работы.

Тогда количество теплоты, которое мы определяли по I закон термодинамике будет равно только чувствительным колебаниям внутренней энергии системы:

\(\;Q=\triangle U\)

Внутренняя энергия при изохорном процессе

Откуда еще раз видно, что количество тепла системы в изохорном процессе будет определяться только изменением внутренней энергии системы, а именно ее начального и конечного состояний.

Примеры

Цикл Отто — это процедура физической стороны, в которой действуют законы термодинамики. В ней описываются манипуляции всего процесса, который выполняет двигатель внутреннего сгорания (ДВС) с воспламенением и последующим воспламенением сжатой смеси от стороннего источника энергии – это цикл, по которому работают все бензиновые двигатели.

Теоретически немецкий инженер То, работая над этим циклом, создал идеальные условия, при которых цикл состоит из четырех этапов - процессов, показанных на рисунке 2:

1-2 стадия адиабатического сжатия рабочего тела

2-3 стадия изохорной подачи тепла к рабочему телу

3-4 стадия адиабатического расширения тела

4-1 стадия охлаждения рабочего тела при постоянном объеме

Также изохорный процесс часто используют для решения физических задач, используя для этого модельные системы. Рассмотрим несколько задач, где используется перводокакзанный закон термодинамики и закон Шарля.

Решение:

Так как разогрев газа по условиям данным нам в задачи идёт при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

\(\frac pT=\;const\)

Откуда

\(\begin{array}{l}\frac{p_1}{T_1}=\frac{\displaystyle p_2}{\displaystyle T_2}\;\\\\\end{array}\)

\(\begin{array}{l}T_2=\;\frac{\displaystyle p_2T_1}{p_1}\\\\\end{array}\)

\(\begin{array}{l}\frac{p_2}{p_1}=1.5\\\\T_2=1.5\ast T_1\;=1.5\ast400\;=\;600\;K\end{array}\)

Ответ: 600 К.

Решение:

Аммиак имеет следующую химическую формулу — NH_3. С помощью таблицы Менделеева рассчитаем его молекулярную массу:

\(M(NH_3)\;=\;M(N)\;+3\ast M(H)\;=\;14\;+\;3\ast1\;=\;14\;+3\;=\;17\;г/моль.\)

Количество теплоты, которое система получает при стабильном объеме, то есть в ходе изохорного процесса (по условию), можно рассчитать следующим образом:

\(Q_p=n\ast C_v\ast\triangle T=n\ast C_v\ast(T_2-T_1)\;=\;\frac{m(NH_3)}{M(NH_3)}\ast C_v\ast(T_2-T_1).\)

Для определения C_v –теплоемкости газа необходимо вспомнить, что аммиак — это химическое вещество, геометрия которого — треугольная пирамида. Таким образом, молекулярная теплоемкость идеального газа для изохорного процесса без учета колебательных степеней свободы (потому что низкие температуры, и они заморожены) для нелинейной многоатомной молекулы будет равно:

\(C_v=3\ast R\)

Подставляем все известные значения в формулу нахождения количества теплоты и находим ее значение:

\(Q_p=\frac{8,5}{17}\ast3\ast8,314\ast(40-25)\;=\;0.5\ast3\ast8.314\ast15\;=\;187\;Дж\\\)

Ответ: 187 Дж теплоты будет затрачено системой на нагрев от 25 до 40 \({}^\circ С\) при постоянном объеме.