Чему равно центростремительное ускорение
Какое явление описывает термин «центростремительное ускорение»
Центростремительное ускорение (также носит название нормального) — один из элементов увеличения быстродействия объекта, который является характеристикой стремительности преобразований векторного направления скорости (второй частью является тангенциальное ускорение, которое является характеристикой перемены модуля скорости).
Центростремительное ускорение обычно ориентировано к центральной части изгиба по траектории. Именно из-за своего направления явление получило такое понятие. Обычно центростремительное ускорение изображают при помощи особого символа \(\[\overrightarrow{a_{n}}\]\) . Показатель n в этом обозначении несет смысл «нормальной» величины. Также возможно обозначать центростремительное ускорение так: \(\[\overrightarrow{w_{n}}\]\) . Единицами измерения для подобной величины служат метры в квадратную секунду (или же \(м\ \[с^{2}\]\) ).
Отличным образцом движения с центростремительным ускорением, что не равняется нулю, является перемещение по окружности. При таком условии \(\[\overrightarrow{a_{n}}\]\) будет ориентировано в центр окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В рамках базовых действий механики обычное (или нормальное) ускорение провоцируется элементами физических сил, которые ориентированы перпендикулярно вектору скорости.
Приведем простой пример: передвижение определенного тела в космосе на орбите можно охарактеризовать при помощи центростремительного ускорения, которое стимулируется гравитационными силами. Включающая совокупность физических сил, которая обусловливает существование обычного ускорения, носит название центростремительной силы. Термин, который связан с центростремительной силой, для неинерциальных систем отчета, центробежная сила.
Центробежная (центростремительная) сила — та сила, которая воздействует на объект, заставляя его совершать перемещение.
Осестремительное ускорение, которое рассматривается при условии осевого движения объекта вокруг собственной оси, в отображении на плоскость, что является перпендикулярной оси, можно считать центростремительным.
Происхождение термина
Самые первые уравнения, которые были верны для вычисления центростремительного ускорения, были выведены Христианом Гюйгенсом, ученым голландского происхождения.
Христиан Гюйгенс — физик, механик, изобретатель, астроном голландского происхождения. Являлся первым представителем от иностранных государств в рядах Лондонского королевского общества, был также представителем Французской академии наук с первого дня основания этого объединения, а также самым первым предводителем этого объединения. Считается пионером теории вероятностей, а также теоретических основ механики. Активно развивал многие направления в физике. Так им разработаны теории в области оптики, астрономии, молекулярной физики, а также геометрии и часового дела. Им впервые были обнаружены кольца у Сатурна, а также им был найден спутник Сатурна — Титан. Также он изобрел часы с маятником, которые можно было использовать в практике. Благодаря его трудам начала развиваться волновая оптика.
Так выглядел Христиан Гюйгенс:
Источник: ru.wikipedia.org
После того, как Христиан Гюйгенс начал собственные исследования в области центростремительного ускорения, многие ученые начали решать задачи в области механики при помощи расчета также и величины центростремительного ускорения, то есть подобные расчеты становятся стандартными для физики.
Формулы Гюйгенса, которые были выведены для центростремительного ускорения, позднее были использованы в качестве основы для формулировки закона всемирного тяготения. В данном законе выражение центростремительного ускорения было использовано для того, чтобы найти теорию зависимости силы гравитации от протяженности до ресурса гравитационный силы. Позднее, из всех этих вычислений получился третий закон Кеплера.
Законы Кеплера — соотношения, которые являются описанием идеальной гелиоцентрической орбиты небесного тела (планеты). Были сформулированы Иоганном Кеплером, ученым немецкого происхождения, на базе продолжительных наблюдений за изменениями астрономических тел Тихо Браге.
Так выглядел Иоганн Кеплер:
К началу 19 века расчет величины центростремительного ускорения превращается в базовые расчеты для науки в чистом виде, для технических дополнений.
В какую сторону ориентировано центростремительное ускорение
Как уже было сказано выше, ускорение объекта, который совершает передвижение по траектории окружности, при условии постоянной по собственному модулю скоростью, которое ориентировано по окружному радиусу к центру данной окружности, носит название центростремительного ускорения. То есть, ориентировано в центр окружности.
Различные способы нахождения центростремительного ускорения для решения задач
Центростремительное ускорение — элемент полноценных расчетов ускорения конкретного материального объекта, который совершает движение по изгибающейся траектории, что характеризует стремительность перемен ориентации вектора скорости. Иным элементом полноценных расчетов ускорения конкретного материального объекта, как уже было сказано, можно считать тангенциальное ускорение, что является показателем перемены значения скорости. Центростремительное ускорение возможно обозначить при помощи такого символа: \(\[\overrightarrow{a_{n}}\]\). Центростремительное ускорение также носит название нормального ускорения.
Величина центростремительного ускорения может быть рассчитана так: \(\[\overrightarrow{a_{n}}=\frac{v^{2}}{r^{2}}\overline{r}=\frac{v^{2}}{r}\overline{e_{r}}\]\)
В данной формуле \(\[\overline{e_{r}}=\frac{\overline{r}}{r}\]\) является одинарным вектором, что ориентирован от центра изгиба траектории к точке, которую надо рассчитать; «r» является радиусом изгиба траектории в области расположение физической точки в определенный временной промежуток, который необходим для расчетов. Первичные правильные вычисления для расчета центростремительного ускорения были совершены Христианом Гюйгенсом.
Единица измерения величины центростремительного ускорения в рамках Международной СИ (системы единиц) — метр, который разделен на квадратную секунду, то есть \(м\ \[с^{2}\]\) .
Формула для вычисления центростремительного ускорения в случае не колебательного (равномерно) передвижения объекта по окружности
Нужно исследовать не колебательное передвижение физического объекта по окружности. В процессе подобного передвижения значение скорости физического объекта не будет изменяться никак \((\[v=const\])\). Однако отсюда не следует, что полноценное ускорение физического объекта в случае подобного передвижения равняется нулю. Ориентация вектора мгновенной скорости будет по касательной к окружности — по данной окружности совершает движение материальный объект. Получается, что в подобном передвижении скорость непрерывно меняет собственную ориентацию. Таким образом, можно сделать вывод, что у материального объекта будет ускорение.
Посмотрите на рисунок:
Источник: webmath.ru
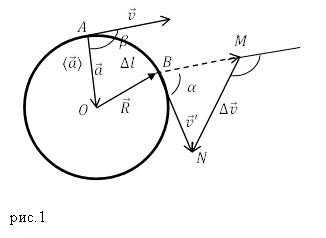
Посмотрите на материальные точки, которые обозначены A и B. Они находятся на пути передвижения частицы. Возможно рассчитать преобразование скорости для этих объектов A и B. Рассчитать можно так:\(\[\triangle\overline{v}=\overline{v^{\backprime}}-\overline{v}\]\) . В случае, когда время, которое тратится на передвижение от объекта A до объекта B, равняется практически нулю, тогда дуга AB не будет практически иметь различий с хордой AB. Получается, что треугольники AOB и BMN будут одинаковы, так: \(\[\frac{\triangle{v}}{v}=\frac{\triangle{l}}{R}=\alpha\]\).
Значение модуля усредненного ускорения можно рассчитать так: \(\[\langle{a}\rangle=\frac{\triangle{v}}{\triangle{t}}=\frac{v\triangle{l}}{R\triangle{t}}\]\).
Теперь нужно рассмотреть предел в случае \(\[\triangle{t}\rightarrow0\]\) от \(\[\langle{a}\rangle\]\) в формуле, что представлена выше: \(\[\alpha=\lim_{\triangle{t}\rightarrow 0}\langle{a}\rangle=\lim_{\triangle{t} \rightarrow 0}\frac{v\triangle{l}}{r\triangle{t}}=\frac{v}{R}\lim_{\triangle{t} \rightarrow 0}\frac{\triangle{l}}{\triangle{t}}=\frac{v}{R}v=\frac{v^{2}}{R}\]\).
Вектор усредненного увеличения скорости формирует с вектором базовой скорости равным угол: \(\[\beta=\frac{\pi+\alpha}{2}\]\). В случае \(\[\triangle{t}\rightarrow0\]\) угол \(\[\alpha\rightarrow0\]\). Можно сделать вывод, что вектор стремительного увеличения скорости формирует с вектором нормальной скорости угол в \(\[\frac{\pi}{2}\]\).
Нам известно, что физический объект, который не прерываясь перемещается по окружности, имеет ускорение, что имеет ориентацию к центру фигуры \(\[(\overline{a_{n}}\perp\overline{v})\]\). Значение ускорение эквивалентно квадратной величине скорости, которая делится на окружной радиус: \(\[a_{n}=\frac{v^{2}}{R}=w^{2}R\]\). В данной формуле w является угловой скоростью передвижения физического объекта \(\[v=w\times{R}\]\). В форме векторов формулу расчета центростремительного ускорения возможно вот так представить:
\(\[\overline{a_{n}}=-w^{2}\overline{R}\]\)
В данной формуле R является вектором радиуса, который эквивалентен по собственной длине радиусу окружной дуги, что имеет направление от центра изгиба к расположению физического объекта, что нужно найти.
Способ расчета центростремительного ускорения при помощи величины угловой скорости
Угловая скорость — измерение в физике, которое эквивалентно соотношению поворотного угла к временному промежутку, в который совершили данный поворот: \(\[\omega=\frac{\gamma}{t}\]\). Единицей измерения для этой величины является рад/с.
Главные специфические особенности угловой скорости
Из-за того, что за промежуток T поворот угла \(\[\gamma=2\pi\]\), тогда угловая скорость соотносится с частотой и периодов поворота: \(\[\omega=\frac{2\pi}{T}\], \[\omega=2\pi{n}\]\).
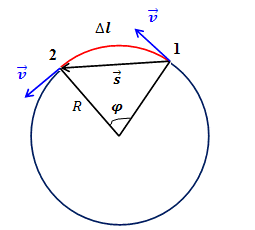
Так выглядит угловой и линейным поворот в процессе передвижения объекта по окружности:
Вместе с термином «угловая скорость» для того, чтобы охарактеризовать не колебательное перемещение по окружности, используется базовый термин «скорость перемещения» объекта по траектории, что можно назвать при таком условии линейной скоростью. Модуль линейной величины передвижения эквивалентен соотношению протяженности окружной дуги \(\[\triangle{l}\]\) к временному отрезку, то есть к времени, что было потрачено на прохождение данной дуги.
Линейная скорость объекта, что передвигается по окружности, не меняется по собственному модулю, только постоянно меняется по ориентации. Она также в произвольных точках траектории ориентирована по касательной к данной дуге окружности, что хорошо видно на рисунке выше.
Линейная и угловая типы скорость соотношения при помощи следующей формулы: \(\[v=\omegaR\]\). В данной формуле R является окружным радиусом.
Закон передвижения объекта по окружности: \(\[\gamma=\gamma_{0}+\omega{t}\]\).
Центростремительное ускорение возможно рассчитать при помощи величины угловой скорости по такой формуле: \(\[\overrightarrow{a_{n}}=\frac{\overrightarrow{v_{2}}-\overrightarrow{v_{1}}}{t}\]\).
Способ расчета центростремительного ускорения при помощи величины периода обращения
Определение 3
Период обращения — затраченные временные ресурсы на то, чтобы совершить один полноценный оборот по окружности. К периоду T возможно применить такую формулу: \(\[T=\frac{2\pi{r}}{v}\]\). Частотой обращения называют значение, которое противоположно периоду, то есть: \(\[v=\frac{1}{T}\]\).
Частота является показателем количества полноценных оборотов физического тела за одну секунду. Единицей измерения частоты являются обороты в секунду.
Представим, что период T=0,1 секунд. Получается, что за этот временной промежуток тело производит полноценный оборот. Частота в таком случае будет равняться \(v= \[\frac{1}{0,1}\]=10\). Получается, что за 0,1 секунду тело может сделать 10 полноценных оборотов.
Формула 5
Так вычисляется центростремительное ускорение при помощи периода обращения: \(\[a=\frac{4\pi^{2}r}{T^{2}}\]\) . А так при помощи частоты: \(\[a=4\pi^{2}n^{2}r\]\)
Через радиус
Формула, при помощи которой возможно вычислить значение центростремительного ускорения выглядит так: \(\[a_{n}=\frac{v^{2}}{R}\]\). В данной формуле v является стремительной скоростью, R является радиусом изгиба траектории.
Возможно вычленить стремительную скорость из формулы угловой скорости:\(\[v=\omega\times{R}\]\) . Теперь возможно добавить ее к основной формуле, сделав расчеты центростремительного ускорения: \(\[a_{n}=\frac{(\omega\times{R})^{2}}{R}=\omega^{2}\times{R}\]\).
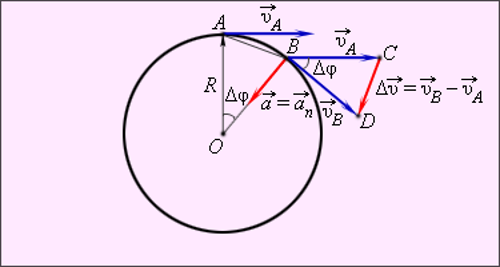
При помощи геометрических расчетов также возможно вычислить значение центростремительного ускорения. Посмотрите на окружность, по которой совершает движение материальный объект:
Источник: ege-study.ru
Нужно избрать как изначальная позиция верхнюю точку. В таком случае вектор стремительной скорость \(\[\overrightarrow{v_{1}}\]\) ориентирован горизонтально. В момент, когда объект совершит движение по дуге, вектор стремительной скорость \(\[\overrightarrow{v_{2}}\]\) станет в положение наклона к первому вектору с углом \(\[\gamma\]\), что эквивалентен угловой дистанции.
Так центростремительный вектор станет базой для построения равнобедренного треугольника, у которого будет угол при вершине \(\[\gamma\]\), а также стороны \(\[\overline{v_{A}}=\overline{v_{B}}\]\). Представим длину основания треугольника в качестве \(\[\triangle{v}\]\). Похожий треугольник, у которого сторона R, возможно рассмотреть внутри окружности. Вершина данного треугольника будет соотноситься с центром фигуры.
Теперь необходимо найти подобие двух треугольников при помощи такой формулы: \(\[\frac{R}{v\times\triangle{t}}\approx\frac{v}{\triangle{v}}\]\). В данной формуле \(\[v\times\triangle{t}\]\) является расстояние, что было проделано объектом в течение движения по дуге, которая практически равна хорде. Возможно переделать формулу так: \(\[\frac{\triangle{v}}{\triangle{t}}\approx\frac{v^{2}}{R}\]\).
При учете небольшого углового интервала, возможно сказать, что вектор\(\[\triangle\overrightarrow{v}\]\) ориентирован на центр окружности. Значит:\(\[\overrightarrow{a_{n}}=\frac{\triangle\overrightarrow{v}}{\triangle{t}}\]; \[\triangle{t}\rightarrow0\]; \[a_{n}=\frac{v^{2}}{R}\]\) .
Отличный вариант для того, чтобы понять, как работает центростремительное ускорение — представить на определенном примере его действие. У нашей планеты Земля центростремительное ускорение равняется 0,03 метра в секунду в квадрате. Таким образом, при условии отсутствия центростремительного ускорения на планете, земля уходила бы из-под ног у человека со скоростью 3 сантиметра в секунду.
В чем измеряется
Центростремительное ускорение обычно помечается таким символом: \(\[\overrightarrow{a_{n}}\]\). Подобный знак был избран учеными для обозначения этой величины, к нему прибавляется n, что служит обозначением нормального ускорения. Также часто используют обозначение центростремительного ускорения как: \(\[\overrightarrow{w_{n}}\]\). В системе измерительных единиц центростремительное ускорение замеряют в метрах в квадратную секунду (то есть\(м\ \[с^{2}\]\) )
Модуль центростремительного ускорения формула
Модуль центростремительного ускорения возможно вычислить так: \(\[\mid{a}\mid=\frac{v^{2}}{R}\]\).
Задачи
Машина совершает движение по участку дороги, который имеет закругление. Радиус у этого закругления равняется 50 метрам. Нужно найти, с какой скоростью двигался автомобиль, если известно, что центростремительное ускорение равнялось 2 метрам в квадратную секунду.
Решение:
R=50 м.
a=2 метра в квадратную секунду.
Найти нужно v.
\(\[a=\frac{v^{2}}{R}\Rightarrow{v}=\sqrt{aR}=\sqrt{50\times2}=10\]\) м в квадратную секунду.
Ответ: 10.
Каким будет центростремительное ускорение объектов на раме во временной промежуток, который равняется t=4 секунды, при условии, что диск совершает вращение по соотношению: \(\[\gamma{t}=3+2t^{3}\]\). Радиус рамы будет равняться R=0,1.
Решение:
Возможно найти величину центростремительного ускорения объектов рамы при помощи использования классической формулы: \(\[a_{n}=\omega^{2}R\]\). Теперь совершим расчеты угловой скорости при помощи выражения \(\[\gamma{t}=3+2t^{3}\]\). Получится: \(\[\omega=\frac{d\gamma}{dt}=6t^{2}\]\). При условии, что t=4, тогда \(\[\omega(t=4)=96\]\). Возможно сделать расчеты центростремительного ускорения, пользуясь формулой:\(\[a_{n}=96^{2}\times0,1=921,6\]\) метров в квадратную секунду.
Ответ: 921,6.
Человек совершает движение на велосипеде по дороге, разгоняясь до 20 метров в секунду. Какова будет величина центростремительного ускорения объекта рамы колеса, если радиус рамы будет равняться 45 см?
Найдем частоту вращения колес велосипеда: \(\[n=\frac{v}{2\pi{R}}\]=\[\frac{20}{2\pi{0,45}}\]=7,07 c\). Таким образом центростремительное ускорение можно вычислить так: \(\[a_{n}=\frac{v^{2}}{R}=\frac{20^{2}}{0,45}=888\]\)метров в секунду в квадрате.
Ответ: 888 метров в секунду в квадрате.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так