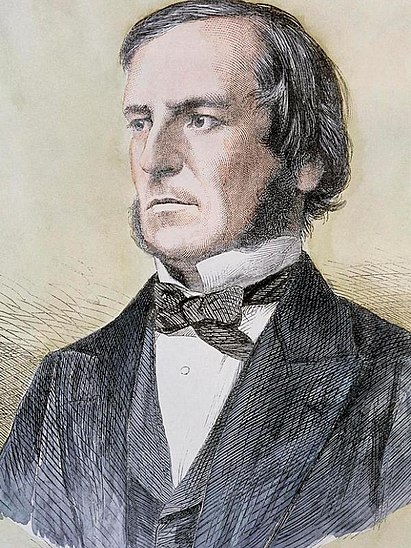Что нужно знать о СДНФ — основные сведения

Что такое СДНФ

Любая булева формула, которая не является тождественно ложной, способна быть приведена к СДНФ. Более того, единственным способом, то есть для любой выполнимой функции в алгебре логики есть собственная СДНФ, притом единственная.

Краткая теория

Представим пример простой ДНФ:

\(F(A,B,C,D,E)=\overline{A}B+A\overline{B}E+B\overline{C}D\)

В структуре ДНФ могут быть повторяющиеся слагаемые, а в структуре каждого слагаемого могут находиться повторяющиеся сомножители. К примеру:

\(F(A,B,C,D,E)=\overline{A}B\overline{B}+A\overline{B}EA+B\overline{C}D+B\overline{C}D\)

Возможно удалить из последнего выражения повторяющиеся сомножители и слагатели таким способом:

\(F(A,B,C,D,E)=\overline{A}BB+A\overline{B}EA+B\overline{C}D+B\overline{C}D=\overline{A}\times(B\overline{B})+(AA)\times{B}E+B\overline{C}D=\overline{A}\times0+A\overline{B}E+B\overline{C}D=A\overline{B}E+B\overline{C}D.\)

Из-за этого ДНФ, у которых наблюдаются повторяющиеся слагаемые и сомножители используются часто только для вспомогательных целей, к примеру, в процессе аналитического преобразования алгебраических выражений. 

Приведем пример СДНФ:

\(F(A,B,C,D,E)=\overline{A}BCDE+A\overline{B}C\overline{D}E+AB\overline{C}D\overline{E}\)

Значение СДНФ проявляется в том, что:

• для каждой определенной функции СДНФ обладает единичным и однозначным характером;
• СДНФ обладает точным соответствием с таблицей истинности функции. Каждое слагаемое СДНФ будет соответствовать одной графе в таблице истинности, в которой функция равняется единице. Так получится, что количество слагаемых в СДНФ будет равно числу единичных значений, которые способна принимать булева функция в собственной области определения;
• СДНФ можно просто получить, исходя из таблицы истинности функции;
• СДНФ крайне удобна как базовое выражение для минимизации функции, просто в ней находятся слагаемые, которые пригодные для «склейки».

\({\displaystyle F(A,B,C,D,E)={\bar {A}}BCDE+A{\bar {B}}C{\bar {D}}E+AB{\bar {C}}D{\bar {E}}.}2\). Алгоритмы построения СДНФ

Построение СДНФ по таблице истинности

Что нужно делать, чтобы найти СДНФ по таблице истинности? Основная схема построения:

1. В таблице истинности нужно отметить конкретный список переменных, на которых значение функции будет равно единице.
2. Для каждого найденного набора нужно записать конъюнкцию абсолютно всех переменных по такому правилу: если значение некоторой переменной будет равно единицы, то в конъюнкцию можно включить саму переменную или же ее отрицание.
3. Далее нужно полученные конъюнкции связать операциями дизъюнкции.

Алгоритм построения СДНФ для булевой функции

Элементы булева множества 0 и 1 обычно рассматривают в качестве логических значений «ложно» и «истинно». В общем случае их рассматривают в качестве формальных символов, которые не обладают конкретным смыслом. Элементы декартова произведения \(B^{n}\) можно назвать булевыми векторами. Множество булевых функций от каждого числа переменных обычно обозначают \(P^{2}\), а от n переменных — \(P^{2}(n)\). Булевы функции носят свои названия по имени известного английского математика Джорджа Буля.

Так выглядел Джордж Буль:

Такое соотношение просто проверить при помощи подстановки возможных значений \(x_{i} (0 \) и \(1)\). Данная формула помогает вынести \(x_{i}\) за знак функции. Шаг за шагом вынося \(x_{1}, x_{2}, x_{n}\) за знак \(f(\overrightarrow{x})\), можно получить такую формулу: \(f(\overrightarrow{x})=\neg{x_1}\wedge{\neg{x_2}}\wedge...\wedge{\neg{x_n-1}}\wedge{\neg{x_n}}\wedge{f}(0,0,...,0,0)\vee{\neg{x_1}}\wedge{\neg{x_2}}\wedge...\wedge{\neg}x_{n-1}\wedge{x_n}\wedge{f}(0,0,...,0,1)\vee...\vee{x_1}\wedge{x_2}\wedge...\wedge{x_n-1}\wedge{\neg}x_n\wedge{f}(1,1,...,1,0)\vee{x_1}\wedge{x_2}\wedge...\wedge{x_n-1}\wedge{x_n}\wedge{f}(1,1,...,1)\).

Из-за использования этого соотношения к каждой из переменных увеличивается число конъюнктов в два раза. Так для функции от n переменных получается \(2^{n}\) возможных наборов величин n переменных. Если на каком-то наборе \(f(\overrightarrow{x})=0\), тогда весь соответствующий конъюнкт будет также равняться нулю и из представления этой функции он может быть исключен. Если \(f(\overrightarrow{x})=1\), тогда в конъюнкте значение функции возможно опустить. В итоге для произвольной функции была построена СДНФ.

Пример построения СДНФ

Представим пример построения СДНФ для медианы

1. В таблице истинности отметим список переменных, на которых значение функции будет равным единице.

2. Для каждого выбранного набора нужно записать конъюнкцию для всех переменных по такому правилу: если значение некоторой переменной — единица, то в конъюнкции включают собственно переменную или же ее отрицание.

3. Полученные конъюнкции связываются действиями дизъюнкции. Так \(\langle{x,y,z}\rangle=(x\wedge{y}\wedge{z})\wedge{(\neg{x}\wedge{y}\wedge{z})}\wedge{(x\wedge{\neg{y}}\wedge{z})}\vee(x\wedge{y}\wedge{\neg{z}})\).

Примеры СДНФ для некоторых функций

Стрелка Пирса будет такой: \(x\downarrow{y}=(\neg{x}\wedge{\neg}y)\).

Исключающее или: \(x\oplus{y}\oplus{z}=(\overline{x}\wedge\overline{y}\wedge{z})\vee(\overline{x}\wedge{y}\wedge\overline{z})\vee(x\wedge\overline{y}\wedge\overline{z})\vee(x\wedge{y}\wedge{z})\).

Совершенная дизъюнктивная нормальная форма формулы \(A (x_{1}, x_{2},…, x_{n})\) носит название ДНФ, которая обладает такими свойствами:

• в ней не существует одинаковых дизъюнктивных элементов;
• ни одна элементарная конъюнкция не обладает двумя одинаковыми высказываниями;
• ни одна элементарная конъюнкция не обладает высказыванием вместе с отрицанием;
• в каждой элементарной конъюнкции есть либо \(x_{i}\), или же \(\overline{x}_{i}, где i=1, n\).

Первое и последнее свойства можно считать достаточными и необходимыми для того, чтобы ДНФ превратилась в СДНФ. Так данные условия дают возможность сформировать алгоритм получения СДНФ из ДНФ:

1. Если у какой-нибудь элементарная конъюнкция нет высказывания \(x_{i}\), тогда можно заменить его выражением \(B\wedge(x_{i}\vee{\overline{x_{i}}})=(B\wedge{x_{i}})\vee(B\wedge{\overline{x_{i}}}\).
2. Если в полученном выражении окажутся одинаковые элементарные конъюнкции, тогда лишние будут опущены.
3. Если в некоторых элементарных конъюнкциях будут совпадать высказывания, тогда лишние будут опущены.
4. Нужно удалить элементарные конъюнкции, в которых находятся высказывания вместе с отрицанием.

Если все элементарные конъюнкции будут таковыми, то есть вся формула будет ложной, тогда она не будет обладать СДНФ.

Алгоритм приведения к СДНФ (как решать выражения с СДНФ)

Существует несколько способов приведения к СДНФ. Первый способ носит название аналитического. Можно привести к СДНФ так:

1. Нужно привести формулу при помощи равносильных преобразований к ДНФ.
2. Далее — удалить члены дизъюнкции, которые содержат переменную вместе с отрицанием (если подобные будут).
3. Из подобных членов дизъюнкции (если подобные будут) нужно удалить все, кроме единственного.
4. Из подобных членов каждой конъюнкции (если подобные будут) нужно удалить все, кроме единственного.
5. Если в определенной конъюнкции не появляется переменная \(x_{i}\) из числа переменных, которые входят в исходную формулу, то следует добавить к данной конъюнкции член \(x_{i}\vee{\overline{x_i}}\).
6. Далее нужно использовать закон дистрибутивности конъюнкции относительно дизъюнкции.
7. Если в итоговой дизъюнкции будут одинаковые члены, тогда нужно удалить все подобные члены, кроме единственного.

Решение.

1. \((x\vee{y})(x\vee{\overline{y}})=x=x(y\vee{\overline{y}})=xy\vee{x}\overline{y}\)
2. \(x(\overline{y}\vee{z})=x\overline{y}\vee{xz}=x\overline{y}(z\vee{\overline{z}})\vee{xz}(y\vee\overline{y})=\mid5\mid=x\overline{y}z\vee{x}\overline{yz}\vee{xzy}\vee{xz\overline{y}=x\overline{y}}z\vee{x}\overline{yz}\vee{xyz}\)
3. \((x\rightarrow{y})xy=(\overline{x}\vee{y})xy=\overline{x}xy\vee{yxy}=xy.\)

Второй способ приведения СДНФ называется табличным. Для приведения нужно составить таблицу истинности для этой функции. Представим алгоритм приведения:

1. Нужно построить таблицу значений формулы.
2. Нужно рассмотреть исключительно такие строки, в которых величины формулы будут равны единице.
3. Нужно убедиться, что каждой строке будет соответствовать конъюнкции всех аргументов (без повторений).
4. Аргумент, который принимает значение 0, должен входить в конъюнкцию с отрицанием, значение единицы должно быть без отрицания.
5. Так следует образовать дизъюнкцию всех конъюнкций.

Нужно рассматривать исключительно наборы 4, 5 и 7, потому что только на данных наборах формула принимает величину, которая равняется единице. У СДНФ будет следующий вид: \[F=x\overline{yz}\vee{x}\overline{y}z\vee{xyz}\].

Для второго уравнения \[F=(x\rightarrow{y})xy\] нужно построить таблицу истинности.

СДНФ (1): №3: F=xy.

Также стоит упомянуть алгоритм приведения СКНФ (совершенная конъюнктивная нормальная форма):

1. Нужно отметить в таблице истинности список переменных, величины функции F на которых будет равно 0.
2. Нужно записать для всех списков отмеченных дизъюнкцию всех переменных — в том случае, когда величина некоторой переменной в данном наборе будет равно 0, в дизъюнкцию включается собственно переменная, если происходит обратная ситуация, тогда в дизъюнкцию включается отрицание.
3. Нужно связать дизъюнкции операциями конъюнкции.
4. Доказательство эквивалентности

определение 3

Эквивалентность — алгебраический термин, который обозначает, что две и более формул представляют одну и ту же функцию. Для того, чтобы обозначить эквивалентность нужно использовать такие математические знаки: \[\equiv\], \[=\], \[\Leftrightarrow\].

Для доказательства эквивалентности формул возможно воспользоваться следующими способами:

1. Первый способ — сравнение и построение таблиц истинности обеих функций. В данной случае итоги будут носить истинных характер только тогда, когда оба высказывания либо истинны, либо ложны.
2. Второй способ — метод эквивалентных преобразований. Смысл данного метода состоял в построении цепи эквивалентности формул на базе ранее доказанных эквивалентностей.

Рассмотрим примеры с некоторыми эквивалентными преобразованиями в области булевой алгебры, а также новыми эквивалентностями, которые можно получить при помощи этих преобразований.

Поглощение

\[x\vee{xy}=x\];

\[x(x\vee{y})=x\].

Доказательство эквивалентности:

\[x\vee{xy}=x\times{l}\vee{xy}=x(l\vee{y})=x\]

\[x(x\vee{y})=xx\vee{xy}=x\vee{xy}=x\]

Склеивание

\[xy\vee{x}\overline{y}=x\]

Доказательство эквивалентности:

\[xy\vee{x}\overline{y}=x(y\vee{\overline{y}})=x\times{l}=x\]

Обобщенное склеивание

\[xz\vee{y}\overline{z}\vee{xy}=xz\vee{y}\overline{z}\]

Доказательство эквивалентности:

\[xz\vee{y}\overline{z}\vee{x}y=xz\vee{y}\overline{z}\vee{xyz}\vee{xy}\overline{z}=xz\vee{y}\overline{z}\]

Расщепление

\[x\vee\overline{x}y=x\vee{y}\]

Доказательство эквивалентности:

\[x\vee\overline{x}y=xy\vee{x}\overline{y}\vee\overline{x}y=xy\vee{x}\overline{y}\vee{xy}\vee\overline{x}y=x\times{l}\vee{y}\times{l}=x\vee{y}\].

Примеры для самостоятельного нахождения СДНФ/СКНФ

задача 1

Нужно привести к СКНФ следующее уравнение: \[((((A\rightarrow{B})\rightarrow\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})\].

При помощи использования закона де Моргана, а также правила \[x\rightarrow{y}=\overline{x}\vee{y}\] можно упростить выражение:

\[F=((((A\rightarrow{B})\rightarrow\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})=(((\overline{A}\vee{B})\rightarrow\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})\]=\[((((\overline{A}\vee{B})\rightarrow\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})=((((\overline{A}\vee{B})\vee\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})\]=\[(((\overline{A}\vee{B})\vee\overline{A})\rightarrow\overline{B})\rightarrow\overline{C})=((((\overline{A}\vee{B})\vee\overline{A})\vee\overline{B})\rightarrow\overline{C})\]=\[((((\overline{A}\vee{B})\vee\overline{A})\vee\overline{B})\vee\overline{C})=(((A\vee{B})\vee\overline{A})\vee\overline{B})\vee\overline{C}\]=\[(((\overline{A}\vee{B})\vee\overline{A})\\wedge{B})\vee\overline{C}=(((A\wedge\overline{B})\vee\overline{A})\wedge{B})\vee{C}\]=\[((A\overline{B}\vee\overline{A})\vee\overline{A})\wedge{B})\vee\overline{C}=(((A\wedge\overline{B})\vee\overline{A})\wedge{B})\vee\overline{C}\]=\[((A\overline{B}\vee\overline{A})\wedge{B})\vee\overline{C}=(A\overline{B}B\vee\overline{A}B)\vee\overline{C}=(0\vee\overline{A}B)\vee\overline{C}=\overline{A}B\vee\overline{C}\].

Нужно привести выражение к КНФ:

\[F=\overline{A}B\vee\overline{C}=(\overline{A}\vee\overline{C})\wedge(B\vee\overline{C})\]

Производим сокращение к СКНФ:

\[F=(\overline{A}\vee\overline{C})\wedge(B\vee\overline{C})=(\overline{A}\vee\overline{C}\vee{B}\overline{B})\wedge(A\overline{A}\vee{B}\vee\overline{C}\]=\[(\overline{A}\vee\overline{C}\vee{B})\wedge(A\vee{B}\vee\overline{C})\wedge(\overline{A}\vee\overline{C}\vee\overline{B})\wedge(\overline{A}\vee{B}\overline{C})\]

задача 2

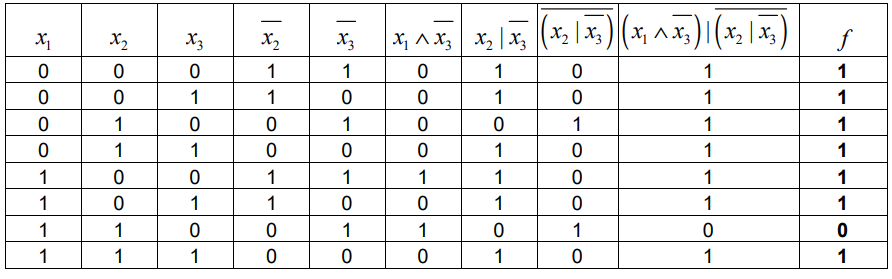
Задается булева функция \[f(x_{1},x_{2},x_{3})=\overline{x_{2}}\vee((x_{1}\wedge\overline{x_{3}}\mid(\overline{x_{2}\mid\overline{x_{3}}}))\]. Необходимо построить таблицу истинности, найти двоичную форму F булевой функции и привести ее к СДНФ.

Решение:

Сделаем таблицу истинности:

Источник: matburo.ru

Двоичная форма функции: F=(11111101). Так СДНФ будет: \[\overline{x_{1}}\overline{x_{2}}\overline{x_{3}}\vee\overline{x_{1}}\overline{x_{2}}{x_{3}}\vee\overline{x_{1}}{x_{2}}\overline{x_{3}}\vee\overline{x_{1}}{x_{2}}{x_{3}}\vee{x_{1}}\overline{x_{2}}\overline{x_{3}}\vee{x_{1}}\overline{x_{2}}{x_{3}}\vee{x_{1}}{x_{2}}{x_{3}}\]