Что такое дискретизация и почему она необходима

Дискретизация в рамках информатики: термин, преимущества

Для решения некоторых задач в курсе информатики нужно трансформировать существующие данные из одних — исходных — формообразований в совершенно иные. К примеру, в процессе прочтения художественной литературы не про себя, а в голос человек трансформирует данные из формы текста в звук. То есть, трансформирует информацию из дискретной в непрерывную форму. Еще одним примером подобного процесса является создание транскрипций, когда звук преобразуется в текст. То есть, происходит трансформация данных из непрерывной формы в дискретную. 

Для хранения, автономной обработки информации и других действий более рационально применять дискретный вид предъявления данных. Это самый главный плюс данного вида предъявления информации. Из-за этого информатика является научной дисциплиной, тесно связанной с компьютерами и инновационными технологиями, которая осознает большую роль дискретизации. 

В рамках информатики под данным термином подразумевают последовательность действий для решения различных проблем и задач. Так, цельный процесс трансформации данных делится на конкретное число более мелких этапов, которые должны быть выполнены друг за другом. Если говорить по-другому, то дискретностью можно назвать алгоритм действий, который имеет жестко регламентируемую, обусловленную правилами и требованиями цепочку шагов. Все остальные действия возможно совершить в рамках алгоритма только после того, как был полностью закончен этап до этого. 

Применимо к функции переменной \(f\left(x\right)\) — изображение данной функции посредством общности n ее величин \(f\left(x_{0}\right), f\left(x_{1}\right),...f\left(x_{n-1}\right)\) на определенном заранее множестве величин аргумента \(x_{0},x_{1},...x_{n-1}\).

В процессе обработки сигналов — изображение альтернативного сигнала, который не прерывается, \(S\left(t\right)\) общностью величин данного сигнала. Эту общность в науке обычно именуют выборкой \(S\left(t_{0}\right), S\left(t_{1}\right), S\left(t_{n-1}\right)\), которые берутся в конкретные временные промежутки \(t_{0}, t_{1}, t_{n-1}\). 

В типичном случае временной промежуток между разными выборками может разниться для обеих пар ближайших выборок, однако часто в процессе обработки сигнала, выборки берутся через установленный или неизменяемый временной промежуток. Данный интервал времени в подобном случае именуется периодом дискретизации или же промежутком выборок. Его принято обозначать при помощи буквы T. Значение, которое обратно периоду дискретизации \(F_{s}=\frac{1}{T}\), именуют выборочной чистотой или же периодичностью дискретизации. 

В качестве примера аналогового сигнала можно упомянуть аудиосигналы, а также видеосигналы, те сигналы, которые источают разные приборы для измерения и т.д. Для дальнейшей цифровой трансформации аналоговые сигналы, которые не прерываются, в обязательно порядке перед этим должны быть подвергнуты процессу дискретизации, а также квантованию (процедуре создания конкретных систем посредством дискретного комплекса значений) в рамках уровня посредством трансформаторов аналого-цифрового типа. 

Наблюдается также и обратная процедура извлечения аналогового сигнала, который никак не прерывается. Он задается заранее дискретной общностью выборок сигнала и именуется восстановлением. Данный процесс совершается посредством трансформаторов цифро-аналогового типа. 

Форматы репрезентации дискретных данных

В целом в науке есть только два формата репрезентации данных. Это дискретный формат и непрерывный формат. Их различия между друг другом колоссальны и зависят от своего происхождения. 

Все объекты или феномены, которые имеют место в реальном мире, возможно изобразить посредством конкретных физических значений и характерных особенностей. Например, циклон, как феномен природы, может быть описан посредством того, насколько силен ветер, какова температура на улице, как много осадков выпало в определенный момент времени и иными характеристиками, которые присущи циклону. 

Так, например, значимыми характеристиками для того, чтобы описать человека являются: 

• сколько человеку лет; 
• какой у него вес; 
• какой рост; 
• какова температура тела; 
• какое у него артериальное давление. 

Все значения, которые были указаны выше и характеризуют человека, обладают своими конкретными минимальными и максимальными величинами. Число показателей, которые могут быть в определенной величине, способно равняться бесконечности. 

Такие значения и данные, которую эти значения транслируют, обычно именуют непрерывными. Между показателями данных величин не существует разрывов в виде скачков. К примеру, величиной, которая не прерывается, является масса тела. У нее могут самые разные показатели от абсолютного нуля до бесконечных величин, в том числе дроби. 

Помимо величин, которые не прерываются, есть такие величины, которые несут в себе значение целого, а не разделенного числа. Так, к примеру, такими величинами являются количество музыкантов в музыкальном коллективе или же количество атомов в молекулах. 

В случае, когда у объекта исследования есть характерная черта в определенные временные промежутки становиться объектом с жестко регламентированными величинами (числа или знаки), то данное свойство именуется дискретными данными объекта. Характерной чертой дискретных данных является неоднородность информации, потенциальность нумерации и изображения в количественном формате с применением логических единицы и нуля. 

Дискретными величинами также можно назвать: 

• число построек в рамках города; 
• фигуры в геометрии; 
• буквы в алфавите. 

Для обладания самыми достоверными и детальными данными об объекте или феномене, обычно они описываются посредством сразу двух форм предъявления данных в одно время. Приведем несколько примеров. 

Дискретные данные обычно изображаются в качестве символов, вместе с этим используются знаки в виде буквенных обозначений и чисел. Посредством натуральных чисел возможно изобразить количество делений на шкале устройства для измерения, номера книжных страниц или же обозначение домов на городской улице. Цифровой тип предъявления данных крайне комфортен в применении для электронно-вычислительных машин. 

В быту помимо чисел человек для изображения данных применяет словесные обозначения, которые составляются из букв определенного (характерного этой местности) алфавита. Посредством слов можно дать обозначение именам и характерным чертам предметов, перечислить виды активности. Очень активно используются разные символы из математики и специальные символы, которые применяют в качестве пунктуационных средств. 

Применение общности различных символов, которые имеют лишь условное обозначение в виде алфавита, помогает создавать разные объекты, несущие информацию. Так: 

• слова состоят полностью из букв, а сами слова могут характеризовать различные значимые черты объектов; 
• посредством цифр возможно передать данные о конкретных (числовых) показателях каких-то величин; 
• посредством применения в одно время цифр, букв, а также символов математики создаются формулы, а также становится возможным указать на отношение разных значений. 

Данный тип предъявления данных носит название символьного, потому что обладает дискретным происхождением. Оно заключается в том, чтобы применять в определенном порядке разные символы. Есть огромное число так называемых алфавитов или же письменных систем, посредством которых становится возможным передавать, записывать и сохранять одинаковые данные, но самыми разными наборами символов. 

Параметры сигнала с точки зрения информационной передачи

Дискретизацией в рамках комплекса информационной обработки является передача данных, что может быть реализована только посредством сигнала. Переносчиками (передатчиками) подобных сигналов могут быть как физические значения, что представляются распространением сигналов в рамках временных и пространственных показателей. Значения подобных временных функций можно считать параметрами сигнала с точки зрения информационной передачи. К подобным параметрам относятся: 

• цвет картинки; 
• расположение основной точки картинки; 
• длина (периодичность) информационных импульсов; 
• долгота распространения импульса в пространстве; 
• повторяемость сигнала; 
• диапазон распространения сигнала; 
• фаза сигнала. 

Процесс дискретизации: главные ступени, алгоритм

Аналогично типу предъявления данных сигналы можно разделить на два вида: 

• аналоговые (те, которые не могут прерваться);
• дискретные. 

Если речь идет об аналоговом типе сигнала, то параметры внутри конкретных пределов обладают способностью принимать абсолютно любые значения в абсолютно любой временной промежуток. Если же речь идет о дискретном сигнале, то всем заданным временным промежуткам находится соответствие в виде конкретной величины показателей. Сигнал дискретного типа дает описание данным, которые не прерываются, в виде точек на графике, который строится в координатной системе. В данном системе абсциссная ось является временем сигнала в форме дискретного типа, а ординатная ось показывает, каково изображение дискретной формой уровня сигнала. 

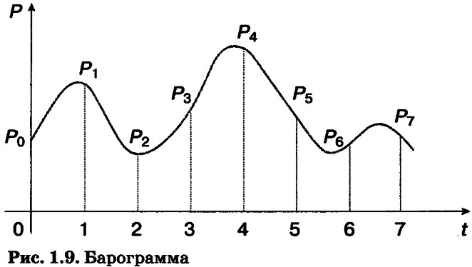
Трансформация из формы аналогового сигнала в форму дискретного типа носит название дискретизация. Она может проводиться как по временному диапазону, так и согласно уровню сигнала. Давайте посмотрим, каким образом работает процесс дискретизации на реальных примерах, например, на приборах, которые самостоятельно записывают показатели атмосферного давления. Данные устройства обычно осуществляют свою работу на метеорологических пунктах. Они постоянно (без перерывов) пишут то, какие изменения в уровне атмосферного давления наблюдаются в течение некоторого количества времени. Данные изменения представляют в виде барограмм, то есть кривых, которые создаются устройством в процессе изменения условий среды.
Посмотрите на один из вариантов барограмм: 

Источник: иванов-ам.рф

Она выглядит таким образом: 

Источник: иванов-ам.рф

Получается, что нам удалось трансформировать данные, которые были получены при исследовании, из аналоговой формы (то есть непрерывной) в дискретный вид. В случае тщательного сопоставления информации таблицы с информацией, которая есть в графике, возможно понять, что была потеряна некоторая точность. Посмотрите, наибольшая величина атмосферного давления наблюдалась на четвертый час проведения эксперимента, однако в таблице этих данных просто нет. 

Для того чтобы сделать процедуру дискретизации более точной, нужно выбирать более маленькие промежутки времени. К примеру, можно получать информацию с барограммы не только один раз в 60 минут, а сократить время до 30 минут или даже до четверти часа. В данном случае исследователь будет обладать более корректными данными, которые потом могут быть переведены в дискретную форму. 

Сигналы в дискретном виде намного проще подвергать обработке и хранить. Более удобно, чем аналоговые данные. Более того, на дискретные данные почти не воздействуют различные препятствия в процессе передачи данных на огромные расстояния. А именно это ценится в информации. Именно из-за этого дискретные сигналы начали использовать очень широко в сопоставлении с непрерывными. 

Какие побочные эффекты могут быть у квантования и процесса дискретизации 

Как было сказано ранее, процесс дискретизации может проводиться как по значению (периодичности) сигнала, так и в рамках временного промежутка. Так, процесс дискретизации по значению очень часто именуют квантованием. В учебниках возможно встретить сразу два понятия — дискретизация и квантование — которые используются для описания процедуры перевода в цифровую форму сигнала. 

После свершения данных манипуляций, каждый сигнал может быть превращен в код, может быть проведена его обработка в цифровой вид, также можно передавать данные на расстояния и сохранять. Иногда появляется нужда в том, чтобы перевести тот сигнал, который был получен, снова в аналоговый вид. Так, к примеру, производится трансляция звука аудиозаписей с различных дисков и т.д. Цифровые сигналы, которые записываются в промежутке с высокой частотой, трансформируются в звуки с низкой частотой. 

Трансформация сигнала в обратную сторону может происходить с конкретным уровнем четкости. Данный уровень находится в прямой зависимости от следующих факторов: 

• того, какой показатель дискретизационной частоты (если показатели частоты растут, то репродукция сигнала становится намного точнее); 
• количество ступеней процесса квантования для всех (по отдельности) выборок (если уровень количества ступеней растет, то и сигнал становится намного более точным). 

Теоретическое обоснование дискретизации 

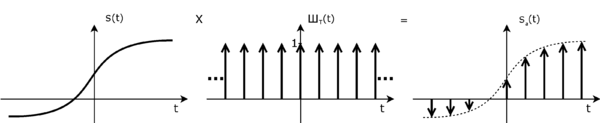
В рамках математики дискретизацией называют перемножение функции, которая не прерывается, \(s\left(t\right)\) на функцию, которая носит название гребень Дирака: \(\triangle{T}\left(t\right)=^{def}\sum_{k=-\infty}^\infty \delta\left(t-kT\right)\) . В данной формуле T является постоянной величиной периода дискретизации, а \(\delta\left(t\right)\) — дельта-функция Дирака: \(s_{a}\left(t\right)=s\left(t\right)\times\sum_{n=-\infty}^\infty \delta\left(t-nT\right)\). 

Трансформация по теореме Фурье дискретной функции \(s_{a}\left(t\right)\) в результате выдает спектр данной функции \(S_{a}\left(f\right)\). Если использовать теорему Котельникова, то получается, что в случае лимитированности спектра \(S\left(f\right)\) изначальной функции, то существует спектральная плотность, которая равна нулю. Она же будет выше части частот \(f_{maz}\), тогда изначальная функция может быть точно восстановлена по общности выборок данной функции, которые были взяты с частотой дискретизации в \(\frac{1}{T}\geq2f_{maz}\) . 

Так выглядит дискретизации при помощи гребня Дирака: 

Источник: ru.wikipedia.org

Для того чтобы полностью восстановить функции, необходимо направить на место, где входят нижние частоты (то есть на фильтр этой области) очередность импульсов, которые бесконечно коротки. У них будет площадь, которая равна по величине выборке. 

Почти нельзя абсолютно точно провести восстановление существующих сигналов по выборкам, потому что: 

• нет сигналов, которые обладали бы ограниченным спектром, потому что существующие сигналы лимитированы по времени, а это вызывает спектр бесконечной ширины;
• физически невозможно создать идеальный фильтр для низких частот; 
• нельзя посылать бесконечно небольшие по длине импульсы на заданную площадь.