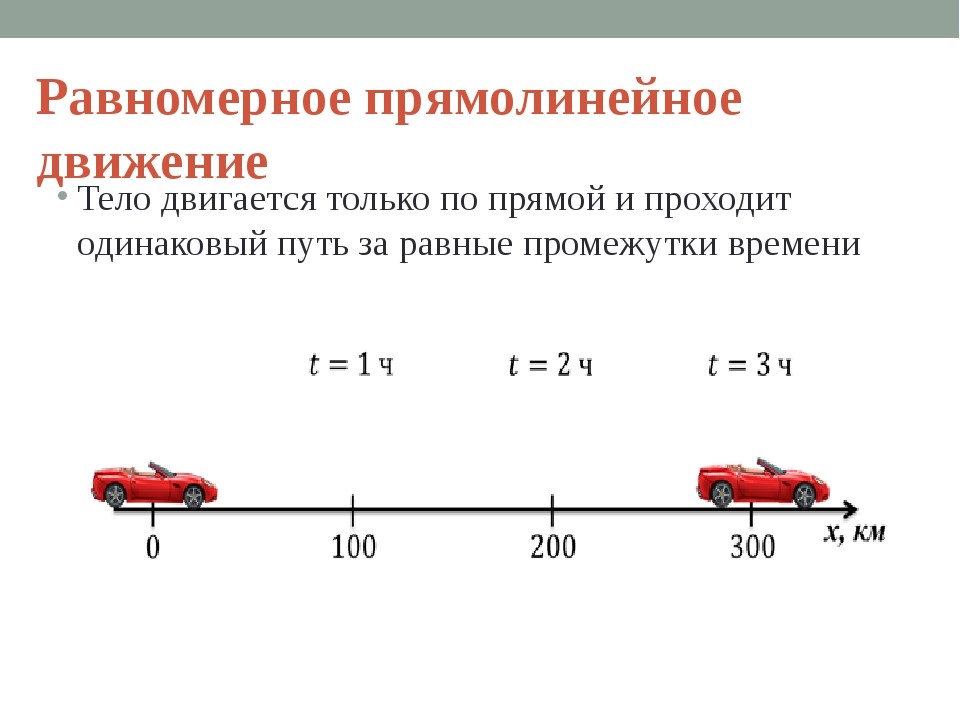
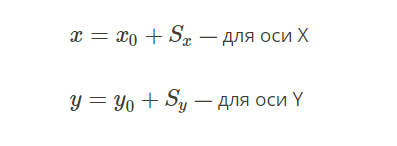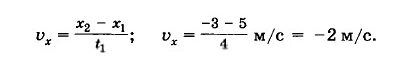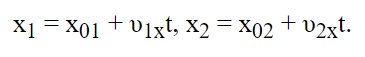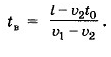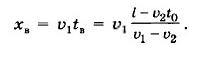Какое движение называют равномерным прямолинейным
Двигаясь по прямой, тело может постепенно снижать скорость своего движения (или она будет возрастать). В этом случае трудно вычислить его местоположение по истечению определенного промежутка времени. Для этого важно уметь пользоваться такой характеристикой механического движения как равномерность.
Закон равномерного прямолинейного движения
Основная задача механики — определение, где находится тело (или предмет) в момент, выбранный для конкретной задачи. Это может касаться прошлого периода, текущего промежутка времени или будущего. Решение поставленной задачи не может быть найдено без знания начальных координат рассматриваемого тела (предмета).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: ds05.infourok.ru
Необходимо учитывать время, прошедшее с начала движения, направление передвижения и то, как далеко продвинулось тело (предмет, группа тел). По расположению конечной координаты определяется, какой характер имело движение.
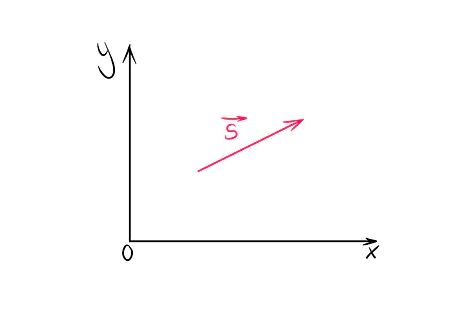
Понятие "перемещение" имеет не только количественную характеристику, но и является векторной величиной. На графике можно видеть следующую картину:
Источник: youclever.org
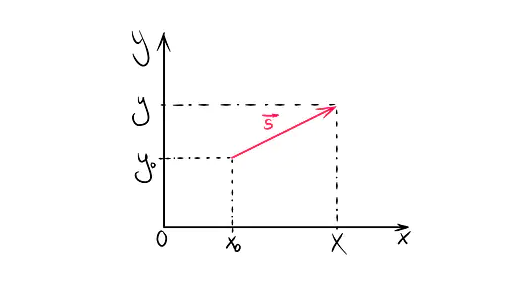
Используя оси координат, были схематически нанесены начальные координаты тела (предмета). При этом нет необходимости прибегать к числам. Достаточно использовать символы: y, x, y0 и x0:
Источник: youclever.org
На диаграмме показано, что если будут опущены перпендикуляры на оси координат, получатся проекции начальной точки движения и той, в которой тело (предмет) очутилось через прошедшее время (отрезок времени выбирается произвольно либо по условию задания). Чтобы получить конечную точку движения, нужно добавить проекцию к точке, соответствующей началу.
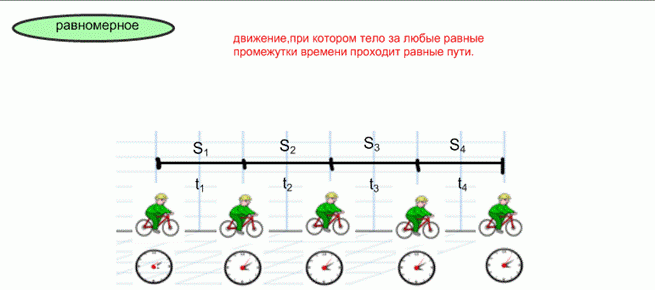
Когда тело (предмет, группа тел) движется по прямой линии, сохраняя свою скорость постоянной (как по модулю, так и по направлению), говорят: оно совершает равномерное прямолинейное движение. Значение пройденных отрезков пути для выбранных (идентичных) временных интервалов одинаково на всех участках.
Источник: urok.1sept.ru
На графике, показанном выше, особенность заключается в том, что ось OX отражает саму линию движения. Тогда именно координата X определяет положение тела.
Важно обратить внимание на однонаправленность векторов скорости и перемещения: движение тела при движении прямолинейно проецируется на ось OX, эти два вектора проявляют свойство параллельности.
Описанные ситуации — проявление закона равномерного прямолинейного движения
По диаграмме понятно: при нахождении тело (предмета) в начальный момент времени в точке X0, а через промежуток t находится — в точке X, его перемещение можно выразить так:
\(ΔS=X-X0\)
С другой стороны:
\(X=X0+Vt\)
Искомая величина может принимать как положительное, так и отрицательное значения. Если тело (предмет) двигалось равномерно и прямолинейно, оно прошло путь, величина которого совпадает с модулем перемещения. Скорость (V) выражается формулой:
\(V=ΔS/Δt=(X-X0)/(t-t0)= const\)
В случае, когда v>0, тело движется в положительном направлении. Оно совпадает с направлением оси OX. Если v<0, по направления противоположны.
Уравнение равномерного прямолинейного движения
Для решения задачи вычисления координат тела в определенный момент времени используются уравнения:
Источник: youclever.org
Когда данные уравнения приемлемы для решения задач, необходимо учитывать, что координатная ось, на которую проецируется движение, параллельна траектории движения. Чаще всего это ось OX. Тогда находить V можно так:
\(V=Δx/Δt=(X-X0)/t\)
Согласно основной особенности равномерного движения, в любые равные моменты времени скорость будет одинаковой. Отличие от координаты: она изменится на ту же величину.
Источник: ds03.infourok.ru
Выполнив соответствующие математические действия, мы получаем окончательную формулировку уравнения прямолинейного равномерного движения:
\(X=X0+Vt\)
Форма уравнения свидетельствует о:
- существующая зависимость линейная;
- прямая, отражающая движение, пересекает ось координат.
Скорость при равномерном прямолинейном движении: формула
Одна из основных величин, задействованных в уравнении равномерного прямолинейного движения, — скорость. Она определяет характер наклона графика. Чем выше значение скорости, тем круче график. Если график направлен вниз, это означает: значение скорости имеет знак «-».
Величина, которая математически выражается отношением перемещения тела к промежутку времени, за который это перемещение произошло, — скорость (V) прямолинейного равномерного движения.
Скорость имеет векторный характер. Ее направление совпадает с направлением конечного перемещения.
По своему определению, скорость — это отношение пути к отрезку времени, за которое произошло перемещение. Единицы измерения скорости определяются в зависимости от:
- если движение выражается в метрах, а время — в секундах, то скорость измеряется в метрах в секунду. Это означает, что за одну секунду тело перемещается на определенное количество метров.
- Движение — в км, а время — в часах, скорость — км/ч.
При равномерном движении скорость - величина постоянна на протяжении совершаемого перемещения.
Источник: mnogoformul.ru
Перемещение при прямолинейном равномерном движении
Формулы ПРД (прямолинейного равномерного движения) — основа для определения скорости и перемещения.
Вернемся к графику, на котором путь (S), пройденный телом за промежуток времени (t), определяется как проекция вектора перемещения на ось OX. Она равна X-Xo. Тогда перемещение (S)= X-Xo.
В то же время из вышеописанной формулы:
X(S)=Vt
Следовательно, V=S/t
Если записать данное выражение в векторной форме, станет понятно, что перемещение и скорость однонаправленны, а модуль перемещения составляет пройденный путь. Измерение перемещения производится в единицах длины: м, км, см и т.п.
Источник: mnogoformul.ru
Самыми простыми задачами в механической физике являются те, в которых требуется определить положение тела (в начале или конце движения), его скорость и время, на протяжении которого оно передвигалось. Сделать это можно с помощью формулы:
Источник: mnogoformul.ru
Примеры решения задач
Однако не при любом виде движения можно использовать данную формулу для определения перемещения. Существует ряд особенностей (рассмотрены ниже, в виде примеров), в которых действия имеют иной характер.
Каков модуль и каково направление скорости тела, если известно, что движение равномерно и происходит вдоль оси OX. С начала движения прошло 4 секунды, а координата изменилась с 5м до -3м.
Решение
Выше было рассмотрено, что отражением модуля и направления вектора являются проекции на оси координат. Поскольку движение характеризуется равномерностью, то проекцию скорости на ось абсцисс можно определить по следующей формуле:
Источник: www.xn--24-6kct3an
Проекция может иметь отрицательный знак. В таком случае скорость точки иметь направление, противоположное положительному по оси OX. Модуль скорости \(V=|Vx|=|-2м/с|=2м/с.\)
Расстояние между пунктами A и B по прямой линии 20 км. Навстречу друг другу из этих пунктов одновременно выехали два автомобиля. Первый имел скорость 50 км/ч, второй — 60 км/ч.
Необходимо определить места положения автомобилей относительно пункта А через полчаса с момента начала движения, а также на каком расстоянии они будут друг от друга в этот момент.
Решение.
Источник: www.xn--24-6kct3an
Автомобили совершают движения, которые можно выразить формулами:
Источник: www.xn--24-6kct3an
Спустя полчаса (0,5ч), их положение математически можно выразить так:
Источник: www.xn--24-6kct3an
Один из автомобилей достигнет точки C, отдаленной от старта движения на 25 км вправо от A. Второй автомобиль достигнет точки D, которая отдалена влево на 10 км. Таким образом, модуль расстояния составит разность их координат:
\(S=|X2-X1| =|-10км-25км|=35км\)
Соответственно пройденные расстояния можно найти по формулам:
\(S1=V1t=50 км/ч*0,5ч=25км\)
\(S2=V2t=60 км/ч*0,5ч=30км\)
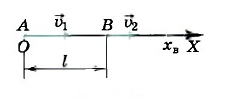
Автомобиль выехал из пункта A в пункт B со скоростью V1. Через время t0 пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V2. Расстояние между пунктами обозначаем S. Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?
Решение
Источник: www.xn--24-6kct3an
Задача № 3
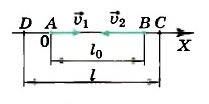
Автомобиль выехал из пункта A в пункт B со скоростью V1. Через время t0 пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V2.
Расстояние между пунктами обозначаем S.
Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?
Решение
При встрече автомобилей их координаты будут равны: X1=X2=Xв
В целом уравнения движения в данном случае выглядят так:
X1=V1t
X2=S+V2(t-t0)
Производя математические действия, получаем:
V1tв=S+V2(tв-t0)
Источник: www.xn--24-6kct3an
Вероятно, V1>V2, S>V2t0
Место встречи автомобилей можно найти по формуле:
Источник: www.xn--24-6kct3an
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так